Stdev.p مقابل stdev.s في excel: ما الفرق؟

هناك ثلاث وظائف مختلفة يمكنك استخدامها لحساب الانحراف المعياري في Excel:

1. STDEV.P: تحسب هذه الدالة الانحراف المعياري للسكان. استخدم هذه الوظيفة عندما يمثل نطاق القيم إجمالي السكان.

تستخدم هذه الدالة الصيغة التالية:

الانحراف المعياري للسكان = √Σ (x _i – μ) ² / N

ذهب:

• Σ : رمز يوناني معناه “المجموع”
• x _i : القيمة ⁱ لمجموعة البيانات
• μ: متوسط عدد السكان
• N: العدد الإجمالي للملاحظات

2. STDEV.S: تحسب هذه الوظيفة الانحراف المعياري للعينة. استخدم هذه الوظيفة عندما يمثل نطاق القيم عينة من القيم وليس مجموعة كاملة من السكان.

تستخدم هذه الدالة الصيغة التالية:

نموذج الانحراف المعياري = √Σ (x _i – x ) ² / (n-1)

ذهب:

• Σ : رمز يوناني معناه “المجموع”
• x _i : القيمة ⁱ لمجموعة البيانات
• x : تعني العينة
• N: العدد الإجمالي للملاحظات

3. STDEV: تحسب هذه الوظيفة أيضًا الانحراف المعياري للعينة. ستُرجع نفس قيمة الدالة STDEV.S تمامًا.

ملاحظة تقنية:

نظرًا لأن صيغة الانحراف المعياري للسكان مقسومة على N بدلاً من n-1 ، فإن الانحراف المعياري للسكان سيكون دائمًا أقل من الانحراف المعياري للعينة.

السبب وراء انخفاض الانحراف المعياري للسكان هو أننا إذا عرفنا كل قيمة سكانية، فإننا نعرف الانحراف المعياري الدقيق.

ومع ذلك، عندما يكون لدينا عينة فقط من السكان، يكون لدينا المزيد من عدم اليقين حول الانحراف المعياري الدقيق لإجمالي السكان، لذلك يجب أن يكون تقديرنا للانحراف المعياري أكبر.

يوضح المثال التالي كيفية استخدام هذه الوظائف عمليًا.

مثال: STDEV.P مقابل STDEV.S في Excel

لنفترض أن لدينا مجموعة البيانات التالية في Excel:

توضح لقطة الشاشة التالية كيفية حساب الانحراف المعياري لمجموعة البيانات باستخدام صيغ الانحراف المعياري الثلاث المختلفة:

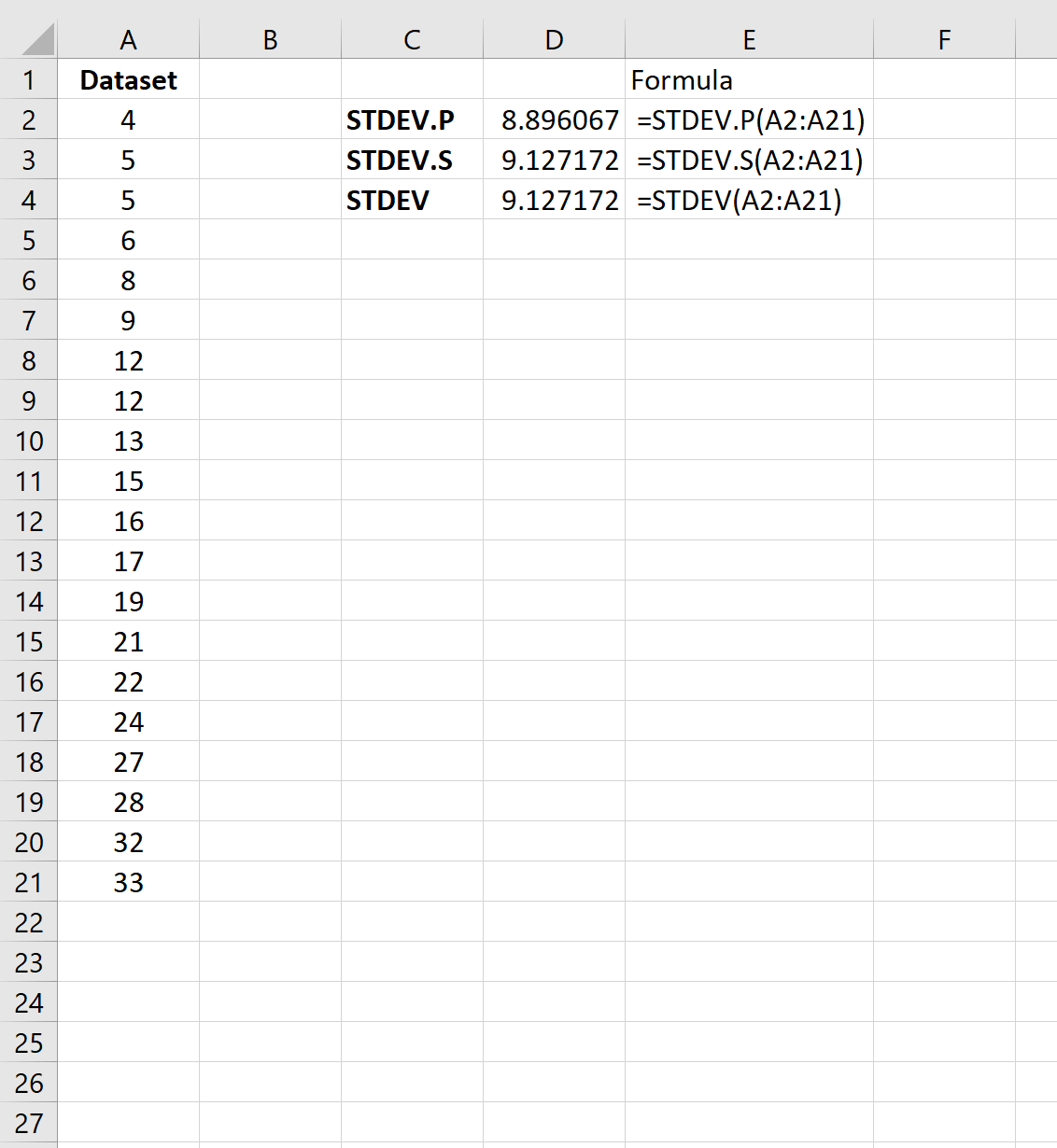
تبين أن الانحراف المعياري للعينة هو 9.127 والانحراف المعياري للسكان هو 8.896 .

كما ذكرنا سابقًا، سيكون الانحراف المعياري للسكان دائمًا أقل من الانحراف المعياري للعينة.

متى يتم استخدام STDEV.P مقابل STDEV.S

في معظم الحالات، لا نكون قادرين على جمع البيانات لجميع السكان. ولذلك نقوم بجمع البيانات فقط لعينة من السكان.

لذلك، نستخدم دائمًا STDEV.S لحساب الانحراف المعياري لمجموعة البيانات، لأن مجموعة البيانات لدينا تمثل عينة بشكل عام.

لاحظ أن STDEV و STDEV.S يُرجعان نفس القيم تمامًا، لذا يمكننا استخدام أي من الدالتين لحساب نموذج الانحراف المعياري لمجموعة بيانات معينة.