الكتابة

By دكتور بنيامين أندرسون زومار 5, 2023 إحصائيات 0 Comments

تشرح هذه المقالة ما يعنيه وصف التوزيع في الإحصائيات. وبالتالي، ستجد تعريف الكتابة، ومثالًا على كتابة المتغير، وبالإضافة إلى ذلك، ستتمكن من التدرب على تمرين تم حله خطوة بخطوة.

ما هي الكتابة؟

في الإحصاء، التطبيع هو عملية يتم فيها تطبيق تحويل خطي على التوزيع بحيث يساوي متوسطه وانحرافه المعياري صفرًا وواحدًا على التوالي.

وبشكل أكثر دقة، تتضمن الكتابة طرح المتوسط من المتغير العشوائي ثم قسمته على الانحراف المعياري.

يمكن أيضًا تسمية الكتابة بالتطبيع أو التوحيد.

صيغة الإدخال

لتصنيف متغير، يجب عليك طرح متوسطه ثم قسمته على انحرافه المعياري. وبالتالي فإن صيغة إدخال المتغير هي كما يلي:

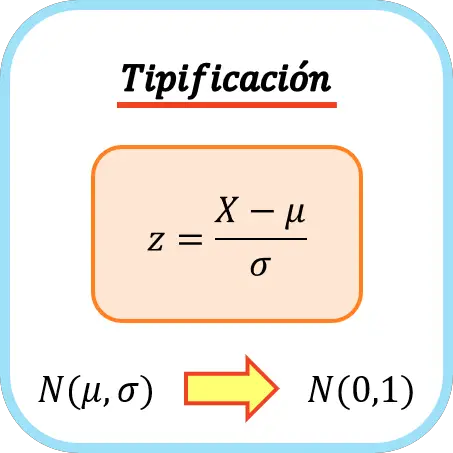
ذهب

$\mu$

هو متوسط المتغير

$X$

$\sigma$

انحرافه المعياري (أو الانحراف المعياري).

ولذلك، فإن الإدخال هو في الواقع تغيير متغير، حيث يتم تطبيق تحويل خطي على المتغير.

إدخال المثال

بالنظر إلى تعريف التصنيف وصيغته، فيما يلي مثال ملموس لفهم المفهوم بشكل كامل.

متغير عشوائي مستمر يتبع توزيعا طبيعيا بمتوسط 45 وانحراف معياري 10، ما احتمال الحصول على قيمة أقل من أو تساوي 60؟

$N(45,10)$

للعثور على احتمال التوزيع الطبيعي نحتاج إلى استخدام جدول خصائصه، ولكن للقيام بذلك نحتاج إلى إجراء عملية الكتابة أولاً. لذلك نطرح المتوسط ونقسمه على الانحراف المعياري إلى قيمة الاحتمال:

$\displaystyle P(X\leq 60)=P\left(Z\leq\frac{60-45}{10}\right)=P(Z\leq 1,5)$

بمجرد توحيدنا، ننتقل إلى جدول احتمالية التوزيع الطبيعي لمعرفة الاحتمال الذي تتوافق معه قيمة 1.5:

كما هو واضح في جدول تصنيف التوزيع الطبيعي، فإن القيمة المحسوبة في الخطوة السابقة تتوافق مع الاحتمال التالي:

$\displaystyle P(Z\leq 1,5)=0,9332$

وبالتالي فإن احتمال الحصول على قيمة تساوي أو أقل من 60 هو 93.32%.

تمرين الكتابة محلول

احسب الاحتمالات التالية للتوزيع الطبيعي الذي يكون متوسطه وانحرافه المعياري 120 و50 على التوالي.

$N(120,50)$

احتمال الحصول على قيمة أقل من أو تساوي 208.
احتمال الحصول على قيمة أكبر من 137.

انظر الحل

في كلا قسمي المشكلة، نحتاج إلى كتابة التوزيع الطبيعي لحساب الاحتمالات.

نبدأ بحساب الكتابة الاحتمالية لقيمة أقل من أو تعادل 208:

$\displaystyle P(X\leq 208)=P\left(Z\leq\frac{208-120}{50}\right)=P(Z\leq 1,76)$

والآن دعونا نلقي نظرة على الجدول أعلاه لمعرفة الاحتمالية التي تتوافق معها القيمة 1.76:

$\displaystyle P(Z\leq 1,76)=0,9608$

ثانياً، سنقوم بحساب احتمال الحصول على قيمة أكبر من 137. وبنفس الطريقة نبدأ بكتابة المتغير:

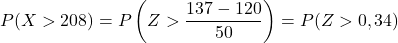$\displaystyle P(X> 208)=P\left(Z>\frac{137-120}{50}\right)=P(Z>0,34)” title=”Rendered by QuickLaTeX.com” height=”43″ width=”398″ style=”vertical-align: -17px;”> <p class=$ ومع ذلك، فإن الجدول المرفق يحتوي فقط على أقل الاحتمالات التراكمية، لذا لاستخدام الجدول يجب علينا أولاً تحويل الاحتمال:

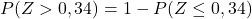$\displaystyle P(Z>0,34)=1-P(Z\leq 0,34)” title=”Rendered by QuickLaTeX.com” height=”19″ width=”252″ style=”vertical-align: -5px;”> <p class=$ وأخيراً نلاحظ من الجدول المرفق الاحتمالية المقابلة للقيمة المحسوبة لـ Z:

$\displaystyle P(Z>0,34)=1-P(Z\leq 0,34)=1-0,6331=0,3669″ title=”Rendered by QuickLaTeX.com” height=”19″ width=”435″ style=”vertical-align: -5px;”> <div class=$

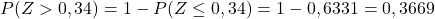
ما هو الهدف من الكتابة؟

لإكمال فهم معنى الكتابة، سنرى فيما يتم استخدامه ومتى يجب كتابة المتغير.

بشكل أساسي، يتم استخدام التقييس لمقارنة قيم التوزيعات بوسائل وتباينات مختلفة. وبالمثل، يتم استخدام التقييس أيضًا لحساب الاحتمال.

ومن خلال توحيد قيمتين للتوزيعات بخصائص مختلفة، يمكننا معرفة القيمة الأكبر أو الأصغر بالنسبة للتوزيع بأكمله. أو بمعنى آخر، من خلال تطبيق عملية التصنيف، يمكننا معرفة القيمة الأقرب أو الأبعد من متوسط توزيعها.

بالإضافة إلى ذلك، كما هو موضح أعلاه، تسمح الكتابة أيضًا بحساب الاحتمالات، نظرًا لأن جداول الاحتمالات بشكل عام تعتمد على توزيع محدد.

About Author

دكتور بنيامين أندرسون

مرحبًا، أنا بنجامين، أستاذ الإحصاء المتقاعد الذي تحول إلى مدرس متخصص في Statorials. بفضل خبرتي الواسعة في مجال الإحصاء، فأنا حريص على مشاركة معرفتي لتمكين الطلاب من خلال Statorials. تعرف أكثر