كيفية إجراء الانحدار الكمي في بايثون
الانحدار الخطي هو أسلوب يمكننا استخدامه لفهم العلاقة بين واحد أو أكثر من متغيرات التوقع ومتغير الاستجابة .
عادةً، عندما نقوم بإجراء الانحدار الخطي، نريد تقدير متوسط قيمة متغير الاستجابة.
ومع ذلك، يمكننا بدلاً من ذلك استخدام طريقة تُعرف باسم الانحدار الكمي لتقدير أي قيمة كمية أو مئوية لقيمة الاستجابة، مثل المئين السبعين، والمئين التسعين، والمئين 98، وما إلى ذلك.
يقدم هذا البرنامج التعليمي مثالاً خطوة بخطوة لكيفية استخدام هذه الوظيفة لإجراء الانحدار الكمي في بايثون.
الخطوة 1: تحميل الحزم اللازمة
أولاً، سنقوم بتحميل الحزم والوظائف اللازمة:
import numpy as np import pandas as pd import statsmodels. api as sm import statsmodels. formula . api as smf import matplotlib. pyplot as plt
الخطوة 2: إنشاء البيانات
في هذا المثال، سنقوم بإنشاء مجموعة بيانات تحتوي على الساعات التي تمت دراستها ونتائج الامتحانات التي تم الحصول عليها لـ 100 طالب في إحدى الجامعات:
#make this example reproducible n.p. random . seeds (0) #create dataset obs = 100 hours = np. random . uniform (1, 10, obs) score = 60 + 2*hours + np. random . normal (loc=0, scale=.45*hours, size=100) df = pd. DataFrame ({' hours ':hours, ' score ':score}) #view first five rows df. head () hours score 0 5.939322 68.764553 1 7.436704 77.888040 2 6.424870 74.196060 3 5.903949 67.726441 4 4.812893 72.849046
الخطوة 3: تنفيذ الانحدار الكمي
بعد ذلك، سنلائم نموذج الانحدار الكمي باستخدام ساعات الدراسة كمتغير متوقع ودرجات الامتحان كمتغير الاستجابة.
سوف نستخدم النموذج للتنبؤ بنسبة التسعين المئوية المتوقعة من درجات الامتحان بناءً على عدد ساعات الدراسة:
#fit the model
model = smf. quantreg ('score~hours', df). fit (q= 0.9 )
#view model summary
print ( model.summary ())
QuantReg Regression Results
==================================================== ============================
Dept. Variable: Pseudo R-squared score: 0.6057
Model: QuantReg Bandwidth: 3.822
Method: Least Squares Sparsity: 10.85
Date: Tue, 29 Dec 2020 No. Observations: 100
Time: 15:41:44 Df Residuals: 98
Model: 1
==================================================== ============================
coef std err t P>|t| [0.025 0.975]
-------------------------------------------------- ----------------------------
Intercept 59.6104 0.748 79.702 0.000 58.126 61.095
hours 2.8495 0.128 22.303 0.000 2.596 3.103
==================================================== ============================
من النتيجة يمكننا أن نرى معادلة الانحدار المقدرة:
المئين التسعون من درجة الامتحان = 59.6104 + 2.8495*(ساعات)
على سبيل المثال، يجب أن تكون النتيجة المئوية التسعين لجميع الطلاب الذين يدرسون 8 ساعات 82.4:
المئين التسعون من درجة الامتحان = 59.6104 + 2.8495*(8) = 82.4 .
يعرض الإخراج أيضًا حدود الثقة العلوية والسفلية للتقاطع وأوقات متغير التوقع.
الخطوة 4: تصور النتائج
يمكننا أيضًا تصور نتائج الانحدار عن طريق إنشاء مخطط مبعثر مع معادلة الانحدار الكمي المجهزة المتراكبة على الرسم البياني:
#define figure and axis
fig, ax = plt.subplots(figsize=(8, 6))
#get y values
get_y = lambda a, b: a + b * hours
y = get_y( model.params [' Intercept '], model.params [' hours '])
#plot data points with quantile regression equation overlaid
ax. plot (hours, y, color=' black ')
ax. scatter (hours, score, alpha=.3)
ax. set_xlabel (' Hours Studied ', fontsize=14)
ax. set_ylabel (' Exam Score ', fontsize=14)
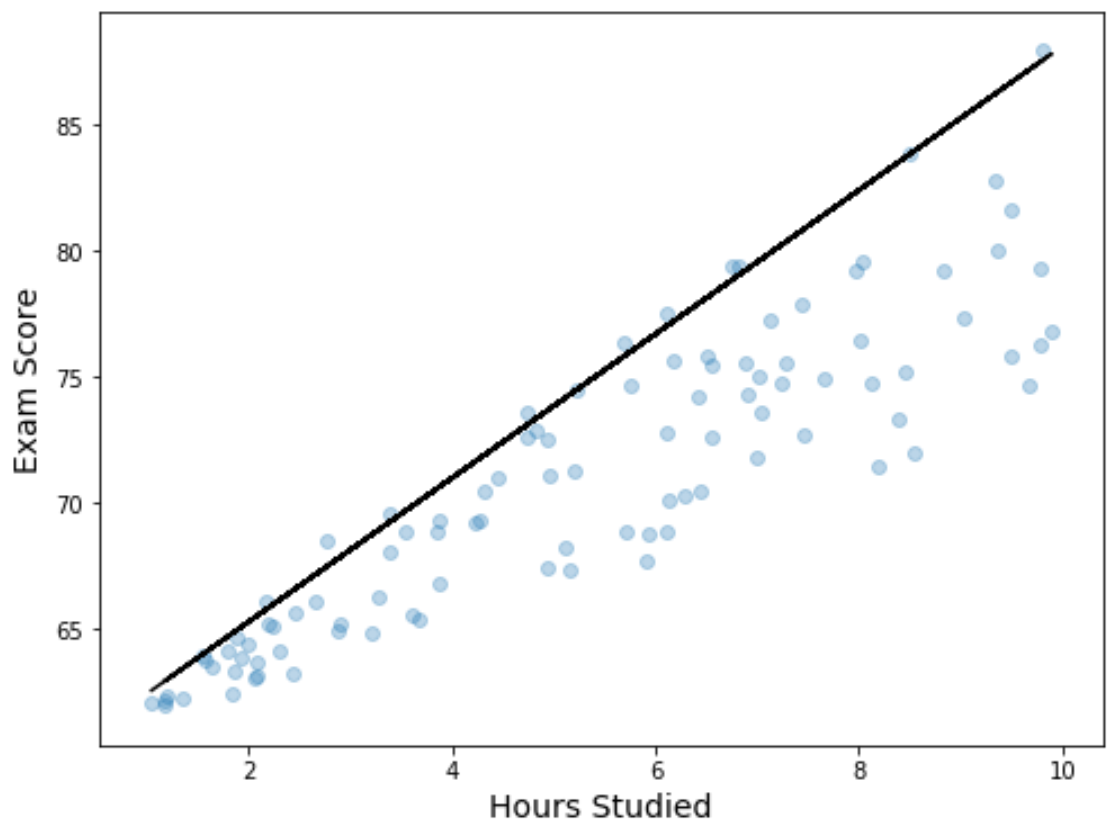
على عكس خط الانحدار الخطي البسيط، لاحظ أن هذا الخط المجهز لا يمثل “الخط الأفضل ملاءمة” للبيانات. وبدلاً من ذلك، فإنه يمر عبر النسبة المئوية التسعين المقدرة في كل مستوى من متغير التوقع.
مصادر إضافية
كيفية إجراء الانحدار الخطي البسيط في بايثون
كيفية إجراء الانحدار التربيعي في بايثون