اختبار breusch-pagan: التعريف والمثال

أحد الافتراضات الرئيسية للانحدار الخطي هو أن البقايا يتم توزيعها بتباين متساوي عند كل مستوى من متغير التوقع. يُعرف هذا الافتراض بالمثلية الجنسية .

عندما لا يتم احترام هذا الافتراض، يقال أن التغايرية موجودة في البقايا. عندما يحدث هذا، تصبح نتائج الانحدار غير موثوقة.

إحدى الطرق لاكتشاف ما إذا كانت التغايرية موجودة بصريًا هي إنشاء مخطط للقيم المتبقية مقابل القيم المجهزة من نموذج الانحدار.

إذا انتشرت البقايا أكثر عند القيم الأعلى في الرسم البياني، فهذه علامة واضحة على وجود التغايرية.

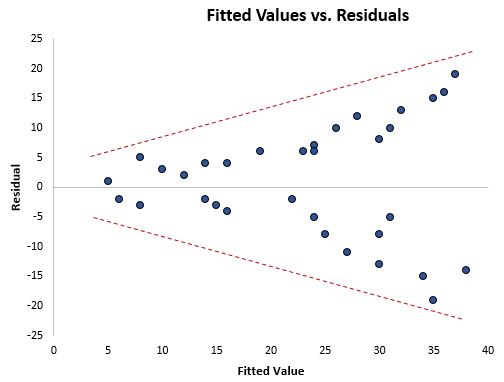
الاختبار الإحصائي الرسمي الذي يمكننا استخدامه لتحديد ما إذا كانت التغايرية موجودة أم لا هو اختبار بروش باغان .

يقدم هذا البرنامج التعليمي شرحًا موجزًا لاختبار Breusch-Pagan بالإضافة إلى مثال.

ما هو اختبار بروش باجان؟

يتم استخدام اختبار Breusch-Pagan لتحديد ما إذا كانت التغايرية موجودة في نموذج الانحدار أم لا.

يستخدم الاختبارالفرضيات الصفرية والبديلة التالية:

• الفرضية الصفرية (H ₀ ): التماثل موجود (يتم توزيع البقايا بتباين متساوي)
• الفرضية البديلة ( _HA ): وجود التغايرية (لا يتم توزيع البقايا بتباين متساوي)

إذا كانت القيمة p للاختبار أقل من مستوى معين من الأهمية (أي α = 0.05)، فإننا نرفض فرضية العدم ونستنتج أن التغايرية موجودة في نموذج الانحدار.

نستخدم الخطوات التالية لإجراء اختبار Breusch-Pagan:

1. تناسب نموذج الانحدار.

2. احسب مربعات بقايا النموذج.

3. قم بتركيب نموذج انحدار جديد، باستخدام مربعات القيم المتبقية كقيم الاستجابة.

4. قم بحساب إحصائية اختبار Chi-square X ² بالصيغة n*R ² _{الجديدة} حيث:

• n: العدد الإجمالي للملاحظات
• R ² _جديد : مربع R لنموذج الانحدار الجديد الذي استخدم مربعات البقايا كقيم استجابة

إذا كانت القيمة p التي تتوافق مع إحصائية اختبار مربع كاي مع درجات حرية p (عدد المتنبئين) أقل من مستوى معين من الأهمية (على سبيل المثال α = 0.05)، فارفض فرضية العدم واستنتج أن التغايرية موجودة .

وبخلاف ذلك، لا ترفض فرضية العدم. في هذه الحالة، يفترض وجود المثلية الجنسية.

لاحظ أن معظم البرامج الإحصائية يمكنها إجراء اختبار Breusch-Pagan بسهولة، لذلك ربما لن تضطر أبدًا إلى تنفيذ هذه الخطوات يدويًا، ولكن من المفيد معرفة ما يحدث خلف الكواليس.

مثال على اختبار Breusch-Pagan

لنفترض أن لدينا مجموعة البيانات التالية التي تحتوي على معلومات عن 10 لاعبي كرة سلة مختلفين:

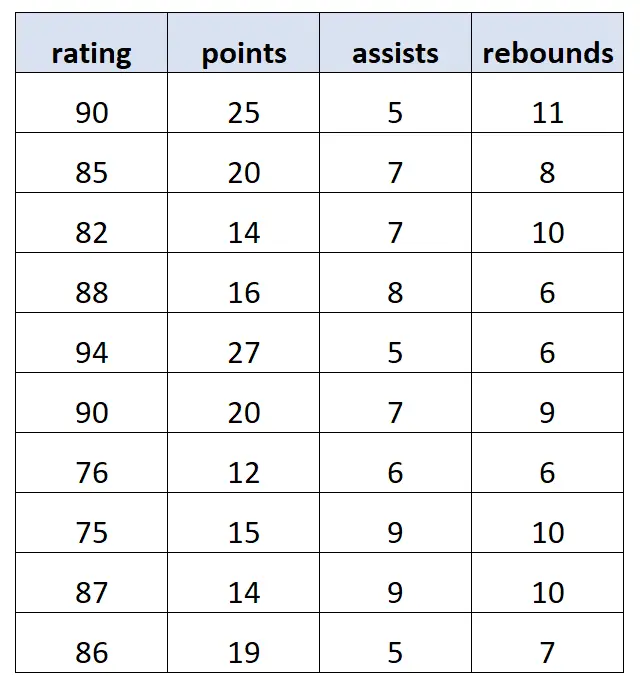
باستخدام البرمجيات الإحصائية، قمنا بمطابقة نموذج الانحدار الخطي المتعدد التالي:

النتيجة = 62.47 + 1.12*(نقاط) + 0.88*(تمريرات حاسمة) – 0.43*(مرتدات)

نستخدم بعد ذلك هذا النموذج لإجراء تنبؤات حول تقييم كل لاعب وحساب البقايا المربعة (أي الفرق المربع بين التقييم المتوقع والتقييم الفعلي):

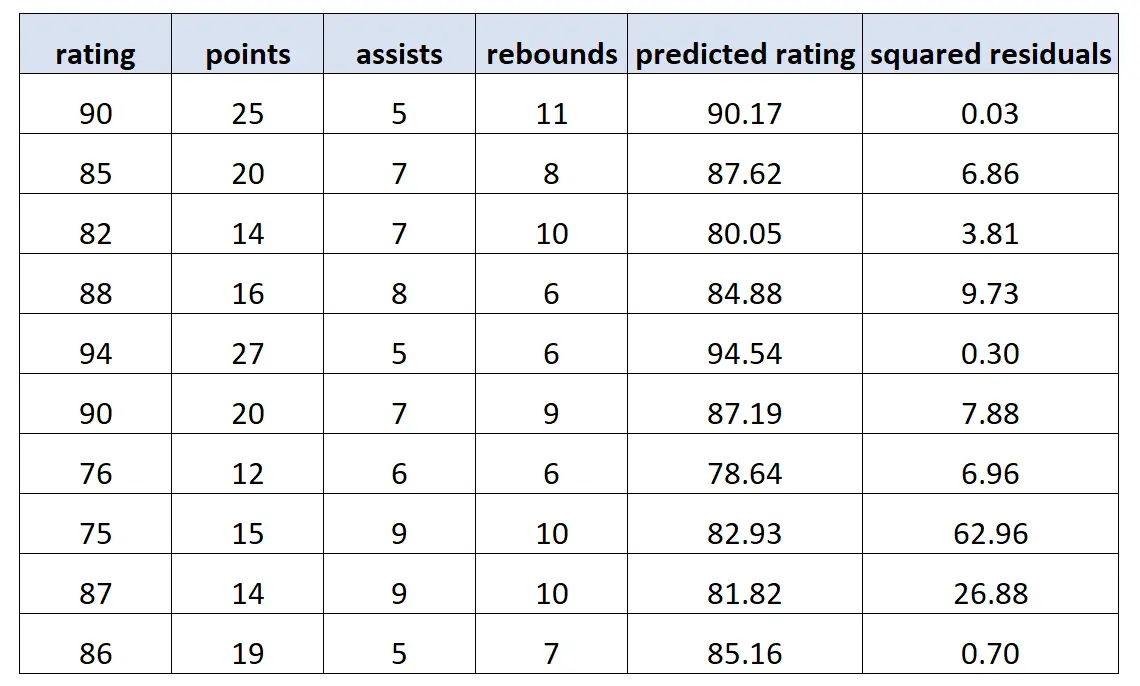
بعد ذلك، قمنا بتركيب نموذج انحدار جديد باستخدام مربعات القيم المتبقية كقيم الاستجابة ومتغيرات التوقع الأصلية كمتغيرات التوقع مرة أخرى. نجد ما يلي:

• ن: 10
• ر ² _جديد : 0.600395

إذن، إحصائية اختبار مربع كاي لاختبار Breusch-Pagan هي n*R ² _new = 10*.600395 = 6.00395 . درجات الحرية هي p = 3 متغيرات متوقعة.

وفقًا لمربع كاي إلى حاسبة القيمة P ، فإن القيمة p التي تقابل X ² = 6.00395 مع 3 درجات حرية هي 0.111418 .

وبما أن هذه القيمة p لا تقل عن 0.05، فإننا نفشل في رفض فرضية العدم. لذلك نفترض أن المثلية موجودة.

اختبار Breusch-Pagan في الممارسة العملية

توفر البرامج التعليمية التالية أمثلة خطوة بخطوة حول كيفية إجراء اختبار Breusch-Pagan في برامج إحصائية مختلفة:

كيفية إجراء اختبار Breusch-Pagan في برنامج Excel
كيفية إجراء اختبار Breusch-Pagan في R
كيفية إجراء اختبار Breusch-Pagan في بايثون
كيفية إجراء اختبار Breusch-Pagan في Stata