كيفية مقارنة المؤامرات الصندوقية: مع الأمثلة

المخطط الصندوقي هو نوع من المخطط يعرض ملخصًا مكونًا من خمسة أرقام لمجموعة بيانات، والذي يتضمن:

• الحد الأدنى للقيمة
• الربع الأول (المئوية الخامسة والعشرون)
• القيمة المتوسطة
• الربع الثالث (المئوي 75)
• القيمة القصوى

لعمل مخطط مربع، نرسم مربعًا من الربع الأول إلى الربع الثالث. بعد ذلك، نرسم خطًا رأسيًا في المنتصف. وأخيرًا، نرسم “شوارب” الربعيات حتى القيمة الدنيا والقصوى.

تعد Boxplots مفيدة لأنها تتيح لنا فهم توزيع القيم في مجموعة البيانات بسرعة. كما أنها مفيدة لمقارنة مجموعتين مختلفتين من البيانات.

عند مقارنة اثنين أو أكثر من المخططات الصندوقية، يمكننا الإجابة على أربعة أسئلة مختلفة:

1. كيف تتم مقارنة القيم المتوسطة؟ يمكننا مقارنة الخط الرأسي في كل مربع لتحديد مجموعة البيانات التي لها قيمة متوسطة أعلى.

2. كيف يمكن مقارنة التشتت؟ يمكننا مقارنة طول كل مربع (الذي يمثل المسافة بين Q1 وQ3 – النطاق الربيعي) لتحديد مجموعة البيانات الأكبر.

3. كيف يمكن مقارنة عدم التماثل؟ كلما اقترب الخط العمودي من الربع الأول، كلما كان انحراف مجموعة البيانات أكثر إيجابية. كلما اقترب الخط العمودي من الربع الثالث، كلما زاد انحراف مجموعة البيانات.

4. هل القيم المتطرفة موجودة؟ في المخططات الصندوقية، عادةً ما يتم تمثيل القيم المتطرفة بدوائر صغيرة تمتد إلى ما وراء كل خط طولي. يتم تعريف الملاحظة على أنها شاذة إذا استوفت أحد المعايير التالية:

• ملاحظة واحدة أقل من Q1 – 1.5*IQR
• الملاحظة أكبر من Q3 + 1.5*IQR

يوضح المثال التالي كيفية المقارنة بين مربعين مختلفين والإجابة على هذه الأسئلة الأربعة.

مثال: مقارنة المؤامرات الصندوقية

تعرض مجموعات البيانات التالية نتائج الطلاب الذين استخدموا إحدى طريقتي الدراسة للتحضير للاختبار:

الطريقة الأولى: 78، 78، 79، 80، 80، 82، 82، 83، 83، 86، 86، 86، 86، 87، 87، 87، 88، 88، 88، 91

الطريقة الثانية: 66، 66، 66، 67، 68، 70، 72، 75، 75، 78، 82، 83، 86، 88، 89، 90، 93، 94، 95، 98

إذا قمنا بإنشاء boxplots لكل مجموعة بيانات، فهذا هو الشكل الذي ستبدو عليه:

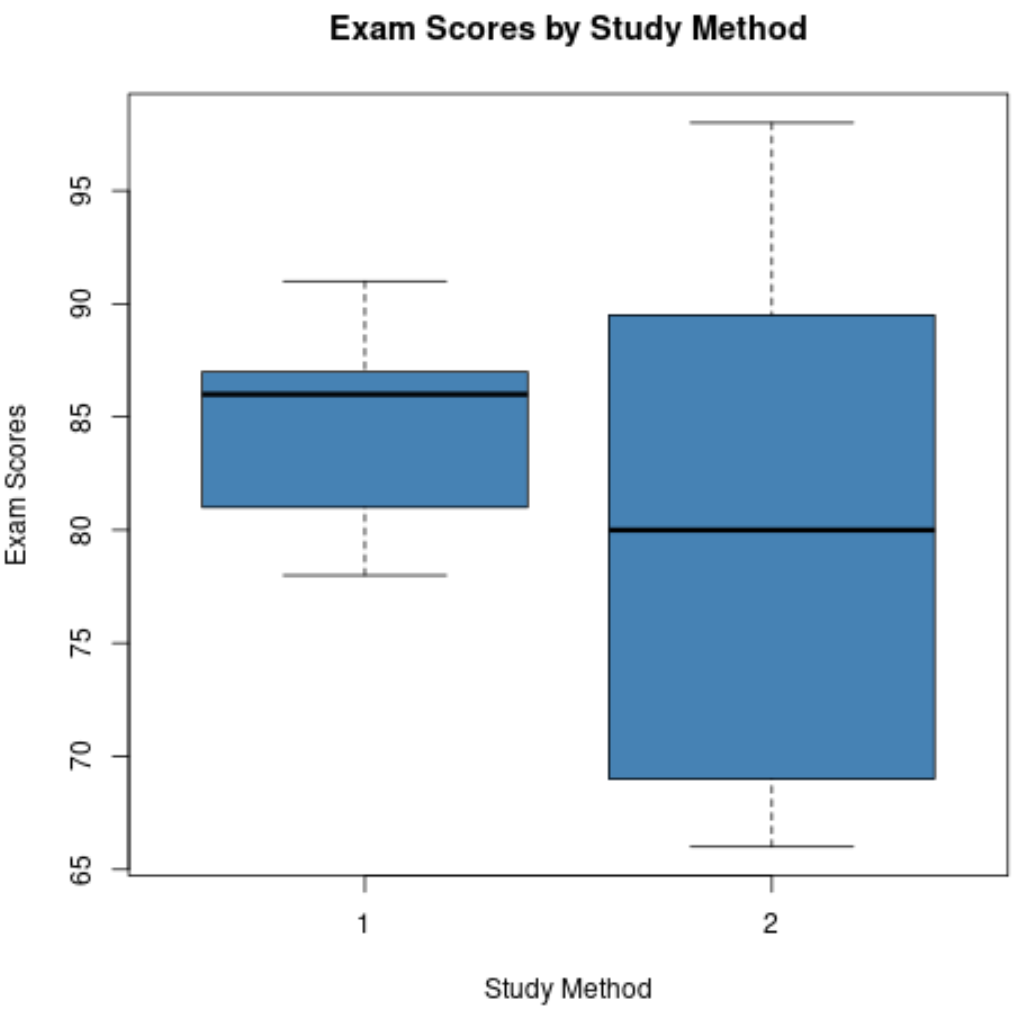
يمكننا مقارنة هذين المخططين الصندوقيين والإجابة على الأسئلة الأربعة التالية:

1. كيف تتم مقارنة القيم المتوسطة؟ الخط الموجود في منتصف مخطط المربع لطريقة الدراسة 1 أعلى من الخط الخاص بطريقة الدراسة 2، مما يشير إلى أن الطلاب الذين استخدموا طريقة الدراسة 1 حصلوا على درجة متوسطة في الامتحانات العليا.

2. كيف يمكن مقارنة التشتت؟ إن المخطط المربع لطريقة الدراسة 2 أطول بكثير من ذلك الخاص بطريقة الدراسة 1، مما يشير إلى أن درجات الامتحانات موزعة بشكل أكبر بين الطلاب الذين استخدموا طريقة الدراسة 2.

3. كيف يمكن مقارنة عدم التماثل؟ الخط الموجود في منتصف مخطط المربع لطريقة الدراسة 1 قريب من Q3، مما يشير إلى أن توزيع درجات الاختبار للطلاب الذين استخدموا طريقة الدراسة 1 منحرف بشكل سلبي. على العكس من ذلك، فإن الخط الموجود في منتصف مخطط الصندوق لطريقة الدراسة 2 قريب من مركز المربع، مما يعني أن توزيع الدرجات منحرف إلى الحد الأدنى.

4. هل القيم المتطرفة موجودة؟ لا تحتوي أي من المخططات الصندوقية على دوائر صغيرة تمتد إلى ما هو أبعد من الشعيرات العلوية أو السفلية، مما يعني أنه لا تحتوي أي من مجموعتي البيانات على قيم متطرفة واضحة.

مصادر إضافية

كيفية إنشاء وتفسير مؤامرات مربع في إكسيل
كيفية إنشاء وتفسير مخططات الصندوق في برنامج SPSS
كيفية إنشاء قطع أرض متعددة في R
كيفية إنشاء وتفسير مؤامرات مربع في ستاتا