الأنواع المتوسطة (الإحصائيات)

By دكتور بنيامين أندرسون زومار 6, 2023 إحصائيات 0 Comments

نوضح هنا ما هي جميع أنواع المتوسطات في الإحصائيات وكيفية حسابها. ستجد الصيغة لكل نوع من أنواع التخزين والأمثلة.

ولكن قبل أن نرى ما هي أنواع المتوسطات، يجب أن نعرف منطقيا ما هو المتوسط في الإحصائيات. لذلك ننصحك بالرجوع إلى الرابط التالي قبل المتابعة.

➤ انظر: ما هو المتوسط (الإحصائيات)؟

ما هي أنواع المتوسطات في الإحصاء؟

في الإحصاء أنواع المتوسطات هي:

المتوسط الحسابي
متوسط الوزن
الوسائل الهندسية
الجذر يعني مربع
المعنى التوافقي
المتوسط المعمم
متوسط f المعمم
وسائل قلصت
المتوسط الرباعي
متوسط الدالة

سنشرح بعد ذلك كيفية حساب جميع أنواع المتوسطات في الإحصائيات. الأنواع الخمسة الأكثر استخدامًا للمتوسط هي المتوسط الحسابي، والمتوسط المرجح، والمتوسط الهندسي، والمتوسط التربيعي، والمتوسط التوافقي. لذلك سوف نتناول المزيد من التفاصيل حول هذه الأنواع الخمسة الرئيسية من الوسائط.

المتوسط الحسابي

يتم حساب الوسط الحسابي عن طريق جمع كافة القيم ثم القسمة على إجمالي عدد نقاط البيانات.

وبالتالي فإن صيغة المتوسط الحسابي هي كما يلي:

$\displaystyle\overline{x}=\frac{1}{N}\sum_{i=1}^N x_i=\frac{x_1+x_2+\dots+x_N}{N}$

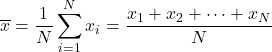
يُعرف الوسط الحسابي أيضًا بالوسط الحسابي .

ربما يكون المتوسط الحسابي هو أكثر أنواع المتوسطات استخدامًا في الإحصاء.

وللاطلاع على مثال لكيفية الحصول على هذا النوع من المتوسط سنقوم بحساب المتوسط الحسابي للبيانات التالية:

$4\quad 7\quad 10\quad 1\quad 8\quad9$

لحساب الوسط الحسابي، ما عليك سوى جمع كافة البيانات الإحصائية وتقسيمها على إجمالي عدد البيانات، وهو 6:

$\overline{x}=\cfrac{4+7+10+1+8+9}{6}=6,5$

متوسط الوزن

لحساب المتوسط المرجح، عليك أولاً ضرب كل بيانات إحصائية بوزنها (أو وزنها)، ثم إضافة جميع المنتجات، وأخيرًا قسمة المجموع المرجح على مجموع كل الأوزان.

وبالتالي فإن صيغة المتوسط المرجح هي كما يلي:

$\overline{x_p}=\cfrac{\sum_{i=1}^N x_i\cdot w_i}{\sum_{i=1}^N w_i}=\cfrac{x_1\cdot w_1+x_2\cdot w_2+\dots x_N\cdot w_N}{w_1+w_2+\dosts +w_N}$

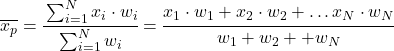
حيث x _i هي القيمة الإحصائية وw _i وزنها المقابل.

أما المتوسط المرجح فهو أكثر صعوبة في الفهم، لذا ننصحك بالاطلاع على المثال التالي الذي يشرح خطوة بخطوة كيفية حسابه:

➤ انظر: مثال على المتوسط المرجح

الوسائل الهندسية

الوسط الهندسي لمجموعة من البيانات الإحصائية يساوي الجذر النوني لحاصل ضرب جميع القيم.

يُستخدم هذا النوع من المتوسط في تمويل الأعمال لحساب معدلات العائد ومتوسطات النسبة المئوية والفائدة المركبة.

صيغة هذا النوع من التخزين معقدة للغاية. في الواقع، لا يمكن حساب المتوسط الهندسي لجميع المجموعات الإحصائية، ولكن في بعض الأحيان لا يمكن تحديد هذا النوع من المتوسط. ولهذا ننصحك بمراجعة جميع الاستثناءات الموضحة في الرابط التالي:

➤ انظر: صيغة الوسط الهندسي

الجذر يعني مربع

جذر متوسط المربع يساوي الجذر التربيعي للوسط الحسابي لمربعات البيانات.

وبالتالي فإن صيغة المربع المتوسط هي كما يلي:

$\displaystyle RMS=\displaystyle\sqrt{\frac{1}{N}\sum_{i=1}^N x_i^2}=\sqrt{\frac{x_1^2+x_2^2+\dots + x_N^2}{N}\vphantom{\sum_{i=1}^N x_i^2}}}$

يُسمى هذا النوع من المتوسط أيضًا جذر متوسط التربيع أو جذر متوسط التربيع أو RMS .

دعنا نشير فقط إلى أن المتوسط المكعب موجود أيضًا، ولكنه يستخدم في حالات خاصة جدًا.

المتوسط المربع له مزايا وعيوب، على سبيل المثال، يكون مفيدًا بشكل خاص عندما يأخذ المتغير الإحصائي قيمًا موجبة وسالبة، لأنه من خلال تربيع كل جزء من البيانات، تصبح جميع القيم موجبة. يمكنك رؤية المزيد من الميزات لهذا النوع من الوسائط من خلال النقر على الرابط التالي:

➤ انظر: مزايا وعيوب جذر متوسط التربيع

المعنى التوافقي

يتم حساب الوسط التوافقي بقسمة العدد الإجمالي للبيانات الإحصائية على مجموع مقلوب كل قيمة.

$\displaystyle H=\frac{N}{\displaystyle\sum_{i=1}^N\frac{1}{x_i}}=\frac{N}{\displaystyle\frac{1}{x_1}+\frac{1}{x_2}+\dots+\frac{1}{x_N}}$

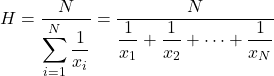
يتم استخدام المتوسط التوافقي لحساب متوسطات السرعات أو الأوقات أو إجراء الحسابات الإلكترونية. هذه الخاصية تميز المتوسط التوافقي عن الأنواع الأخرى من المتوسطات، والتي تستخدم بشكل متكرر في حساب متوسطات الأسعار أو النسب المئوية.

يمكنك الاطلاع على أمثلة لحساب هذا النوع من المتوسط في الصفحة التالية:

➤ انظر: أمثلة على المعنى التوافقي

أنواع أخرى من الجوارب

في هذا القسم سوف نرى الصيغ لأنواع أخرى من الجوارب. لن نخوض في التفاصيل حول كل نوع لأنها غير مستخدمة على نطاق واسع، لكن من الجيد أن تعرف أن هناك أنواعًا أخرى من الجوارب.

المتوسط العام هو خليط من أنواع المتوسطات المذكورة أعلاه ويتم حسابه باستخدام الصيغة التالية:

$\displaystyle\overline{x}(m) = \left ( \frac{1}{N}\cdot\sum_{i=1}^N{x_i^m} \right ) ^{1/m}$

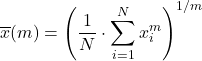
دع f تكون دالة حقنية ورتيبة، ثم يتم تعريف متوسط f المعمم على النحو التالي:

$\displaystyle\overline{x} = f^{-1}\left({\frac{1}{N}\cdot\sum_{i=1}^N{f(x_i)}}\right)$

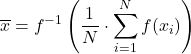
يتضمن المتوسط المقطوع حساب المتوسط الحسابي بعد طرح نسبة مئوية من الملاحظات في الطرفين العلوي والسفلي للعينة. وينبغي رفض نفس النسبة في كلا الطرفين.

لحساب المتوسط الربيعي ، والذي يسمى أيضًا المتوسط الربيعي، يتم أولاً تجاهل البيانات من الربعين الأول والرابع، ثم يتم حساب المتوسط الحسابي للربعين الثاني والثالث للعينة فقط. وبالتالي فإن صيغة هذا النوع من المتوسط هي:

$\displaystyle\overline{x}={2 \over n} \sum_{i=\frac{n}{4}+1}^{\frac{3n}{4}}{x_i}$

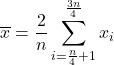
وأخيرًا، يمكنك أيضًا العثور على متوسط دالة . يتم حساب القيمة المتوسطة للدالة المستمرة على فترة مغلقة [a،b] باستخدام الصيغة التالية:

$\displaystyle\overline{f}=\frac{1}{b-a} \int_a^b f(t) dt$

العينة ومتوسط السكان

وأخيرا، سوف نرى ما هو الفرق بين متوسط العينة ومتوسط السكان، وهما نوعان من المتوسطات التي كثيرا ما يتم الخلط بينهما.

متوسط العينة هو المتوسط المحسوب على قيم العينة الإحصائية، أي أنه يتم حسابه على جزء من جميع قيم المتغير.

متوسط السكان هو المتوسط المحسوب على عدد سكان إحصائي، أي على جميع قيم المتغير. ولذلك فإن متوسط المجتمع يتطابق مع التوقع الرياضي للمتغير.

يمكن اعتبار متوسط العينة مساويا عمليا لمتوسط المجتمع إذا كانت هناك كمية كبيرة بما فيه الكفاية من البيانات المعروفة. لكن من الصعب جدًا الحصول على قيمة متوسط السكان، لأنه في الواقع نادرًا ما تكون جميع قيم التوزيع معروفة.

About Author

دكتور بنيامين أندرسون

مرحبًا، أنا بنجامين، أستاذ الإحصاء المتقاعد الذي تحول إلى مدرس متخصص في Statorials. بفضل خبرتي الواسعة في مجال الإحصاء، فأنا حريص على مشاركة معرفتي لتمكين الطلاب من خلال Statorials. تعرف أكثر