كيفية إجراء اختبار عدم اللياقة في r (خطوة بخطوة)

يتم استخدام اختبار عدم الملاءمة لتحديد ما إذا كان نموذج الانحدار الكامل يوفر ملاءمة أفضل لمجموعة البيانات أم لا مقارنة بالإصدار المصغر من النموذج.

على سبيل المثال، لنفترض أننا نريد استخدام عدد ساعات الدراسة للتنبؤ بدرجات الامتحانات للطلاب في كلية معينة. يمكننا أن نقرر تكييف نموذجي الانحدار التاليين:

النموذج الكامل: النتيجة = β ₀ + B ₁ (ساعات) + B ₂ (ساعات) ²

النموذج المخفض: النتيجة = β ₀ + B ₁ (ساعات)

يوضح المثال التالي خطوة بخطوة كيفية إجراء اختبار عدم الملاءمة في R لتحديد ما إذا كان النموذج الكامل يوفر ملاءمة أفضل بكثير من النموذج المصغر.

الخطوة 1: إنشاء مجموعة بيانات وتصورها

أولاً، سنستخدم الكود التالي لإنشاء مجموعة بيانات تحتوي على عدد ساعات الدراسة ودرجات الامتحانات المكتسبة لـ 50 طالبًا:

 #make this example reproducible
set. seeds (1)

#create dataset
df <- data. frame (hours = runif (50, 5, 15), score=50)
df$score = df$score + df$hours^3/150 + df$hours* runif (50, 1, 2)

#view first six rows of data
head(df)

      hours score
1 7.655087 64.30191
2 8.721239 70.65430
3 10.728534 73.66114
4 14.082078 86.14630
5 7.016819 59.81595
6 13.983897 83.60510

بعد ذلك، سنقوم بإنشاء مخطط مبعثر لتصور العلاقة بين الساعات والنتيجة:

 #load ggplot2 visualization package
library (ggplot2)

#create scatterplot
ggplot(df, aes (x=hours, y=score)) +
  geom_point() 

الخطوة 2: ملاءمة نموذجين مختلفين لمجموعة البيانات

بعد ذلك، سنقوم بتركيب نموذجين انحداريين مختلفين لمجموعة البيانات:

 #fit full model
full <- lm(score ~ poly (hours,2), data=df)

#fit reduced model
reduced <- lm(score ~ hours, data=df)

الخطوة 3: إجراء اختبار عدم اللياقة

بعد ذلك، سوف نستخدم الأمر anova() لإجراء اختبار عدم التوافق بين النموذجين:

 #lack of fit test
anova(full, reduced)

Analysis of Variance Table

Model 1: score ~ poly(hours, 2)
Model 2: score ~ hours
  Res.Df RSS Df Sum of Sq F Pr(>F)   
1 47 368.48                                
2 48 451.22 -1 -82.744 10.554 0.002144 **
---
Significant. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

تبين أن إحصائيات اختبار F هي 10.554 والقيمة p المقابلة هي 0.002144 . وبما أن هذه القيمة p أقل من 0.05، فيمكننا رفض الفرضية الصفرية للاختبار ونستنتج أن النموذج الكامل يوفر ملاءمة إحصائية أفضل بكثير من النموذج المخفض.

الخطوة 4: تصور النموذج النهائي

أخيرًا، يمكننا تصور النموذج النهائي (النموذج الكامل) مقابل مجموعة البيانات الأصلية:

 ggplot(df, aes (x=hours, y=score)) + 
          geom_point() +
          stat_smooth(method=' lm ', formula = y ~ poly (x,2), size = 1) + 
          xlab(' Hours Studied ') +
          ylab(' Score ') 

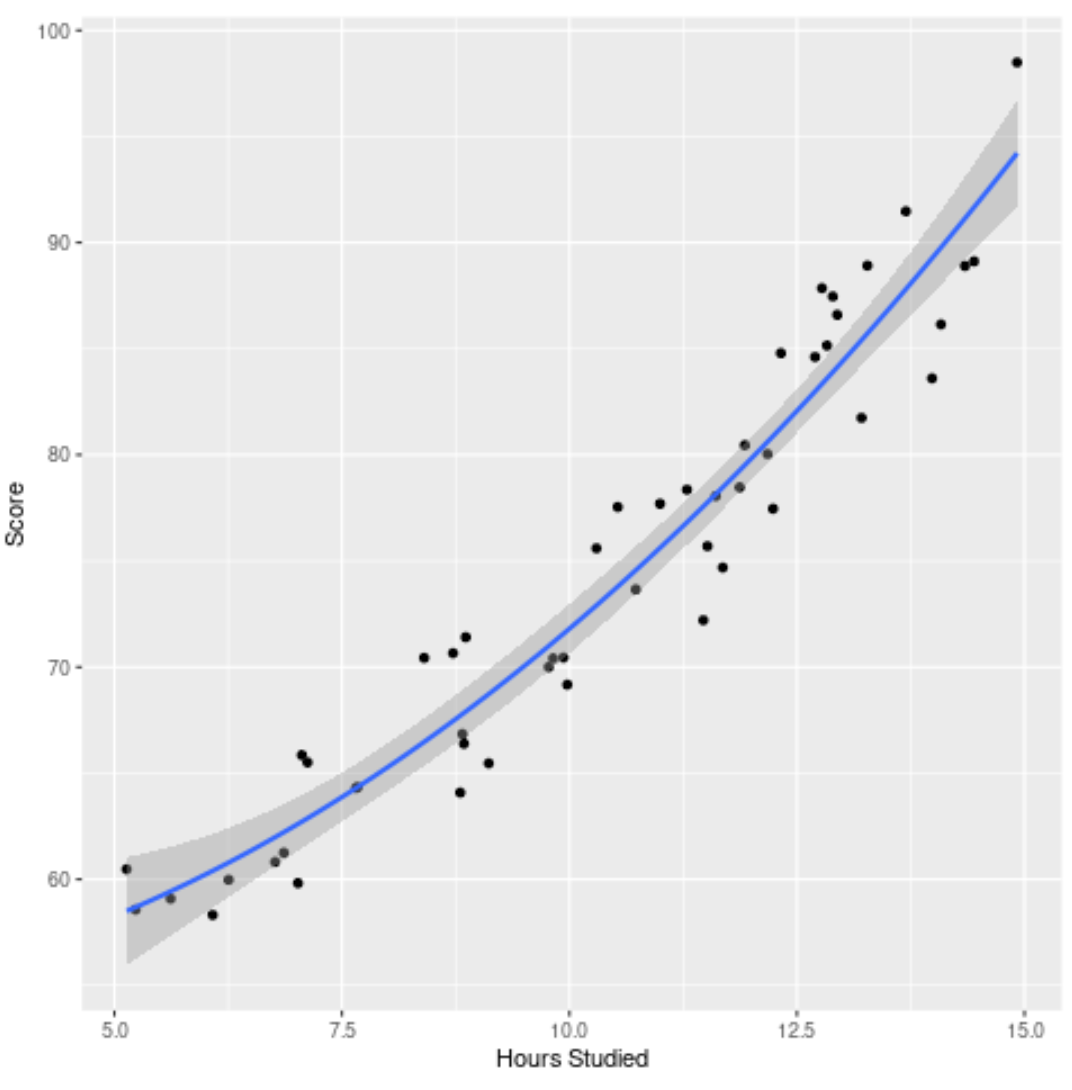
يمكننا أن نرى أن منحنى النموذج يناسب البيانات بشكل جيد.

مصادر إضافية

كيفية إجراء الانحدار الخطي البسيط في R
كيفية إجراء الانحدار الخطي المتعدد في R
كيفية إجراء الانحدار متعدد الحدود في R