ما هي موثوقية النماذج المتوازية؟ (التعريف & #038؛ مثال)

في الإحصاء، تقيس موثوقية النموذج الموازي العلاقة بين شكلين متكافئين للاختبار.

عملية حساب موثوقية النماذج المتوازية هي كما يلي:

الخطوة الأولى: تقسيم الاختبار إلى نصفين.

على سبيل المثال، قم بتقسيم اختبار مكون من 100 سؤال عشوائيًا إلى اختبار أ يحتوي على 50 سؤالًا واختبار ب يحتوي أيضًا على 50 سؤالًا.

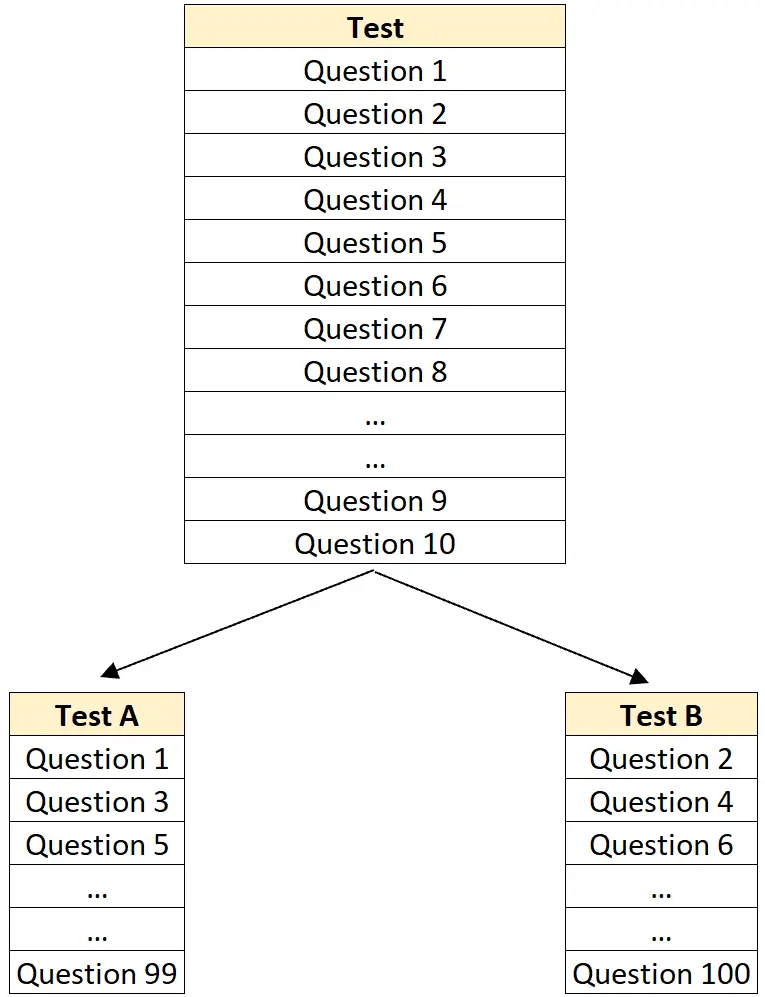
الخطوة الثانية: توزيع النصف الأول على جميع الطلاب، ثم توزيع النصف الثاني على جميع الطلاب.

على سبيل المثال، قم بإجراء الاختبار “أ” على جميع الطلاب العشرين في فصل معين وتسجيل درجاتهم. ثم، ربما بعد شهر، قم بإجراء الاختبار “ب” لنفس الطلاب العشرين وسجل درجاتهم في هذا الاختبار أيضًا.

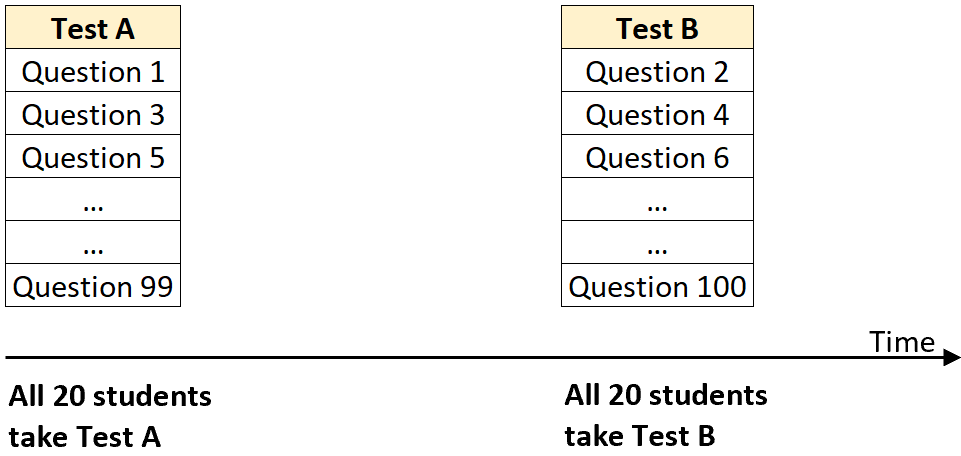
الخطوة الثالثة: حساب الارتباط بين درجات الاختبار للاختبارين.

احسب العلاقة الارتباطية بين درجات الاختبارين. يقال إن الاختبار يتمتع بموثوقية النماذج المتوازية إذا كان الارتباط بين الدرجات مرتفعًا.

متى يتم استخدام موثوقية النماذج المتوازية

غالبًا ما يتم استخدام موثوقية النموذج الموازي في الأوساط الأكاديمية عندما لا يريد الأستاذ أن يتمكن الطلاب من الوصول إلى أسئلة الاختبار مسبقًا.

على سبيل المثال، إذا قام الأستاذ بتوزيع الاختبار “أ” على جميع الطلاب في بداية الفصل الدراسي، ثم قام بتوزيع نفس الاختبار “أ” في نهاية الفصل الدراسي، فيمكن للطلاب ببساطة حفظ الأسئلة والإجابات من الاختبار الأول.

ومع ذلك، من خلال توزيع اختبار B مختلف في نهاية الفصل الدراسي (ونأمل أن يكون بنفس الصعوبة)، يستطيع الأستاذ تقييم معرفة الطلاب مع ضمان عدم رؤية الطلاب للأسئلة مسبقًا.

العيوب المحتملة لموثوقية النموذج الموازي

إن موثوقية النماذج المتوازية لها عيبان محتملان:

1. يتطلب الكثير من الأسئلة.

تعمل موثوقية النماذج المتوازية بشكل أفضل مع الاختبارات التي تحتوي على عدد كبير من الأسئلة (على سبيل المثال، 100 سؤال)، لأن الرقم الذي نحسبه للارتباط سيكون أكثر موثوقية.

2. ليس هناك ما يضمن أن النصفين متوازيان بالفعل.

عندما نقسم الاختبار عشوائيًا إلى نصفين، ليس هناك ما يضمن أن النصفين سيكونان متوازيين أو “متساويين” في الصعوبة. وهذا يعني أن الدرجات قد تختلف بين الاختبارين لمجرد أن أحدهما أكثر صعوبة من الآخر.

موثوقية النماذج الموازية وموثوقية النصف المقسم

تشبه موثوقية الأشكال المتوازية الموثوقية النصفية ، ولكن هناك اختلاف بسيط:

الموثوقية تنقسم إلى قسمين:

يتضمن ذلك تقسيم الاختبار إلى نصفين وإدارة كل نصف لنفس المجموعة من الطلاب. لا يهم الترتيب الذي يؤدي به الطلاب الاختبار.

وميزة هذه الطريقة هي قياس الاتساق الداخلي . ومن الناحية المثالية، نود أن يكون الارتباط بين النصفين مرتفعا، لأن هذا يشير إلى أن جميع أجزاء الاختبار تساهم بالتساوي في ما يتم قياسه.

موثوقية الأشكال المتوازية:

يتضمن ذلك تقسيم الاختبار إلى نصفين – نطلق عليهما “أ” و”ب” – وإدارة كل نصف لنفس المجموعة من الطلاب.

ولكن من المهم أن يؤدي جميع الطلاب الاختبار “أ” أولاً، ثم الاختبار “ب”، حتى لا تقدم معرفة إجابات الاختبار “أ” أي فائدة للطلاب الذين يتقدمون للاختبار “أ” لاحقًا. ب”.

مصادر إضافية

مقدمة سريعة لتحليل الموثوقية
ما هو تقسيم الموثوقية إلى النصف؟
ما هي موثوقية الاختبار وإعادة الاختبار؟
ما هي الموثوقية بين المقيمين؟