مقدمة للتوزيع الموحد

التوزيع الموحد هو توزيع احتمالي يكون فيه لكل قيمة بين الفترة من a إلى b نفس احتمال الحدوث.

إذا كان المتغير العشوائي X يتبع توزيعًا موحدًا، فيمكن العثور على احتمال أن يأخذ X قيمة بين x ₁ و x ₂ من خلال الصيغة التالية:

ف(س ₁ < X < س ₂ ) = (س ₂ – س ₁ ) / (ب – أ)

ذهب:

• × ₁ : قيمة الفائدة الأقل
• × ₂ : القيمة العليا للفائدة
• أ: أقل قيمة ممكنة
• ب: أقصى قيمة ممكنة

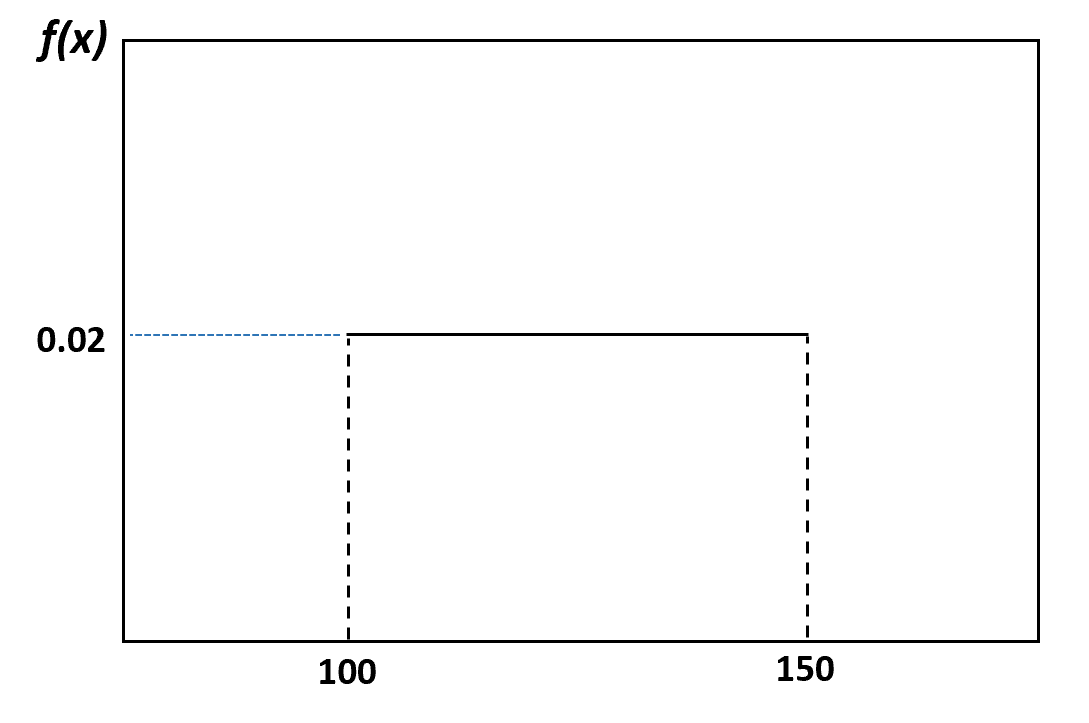
على سبيل المثال، لنفترض أن وزن الدلافين موزع بالتساوي بين 100 و150 رطلاً.

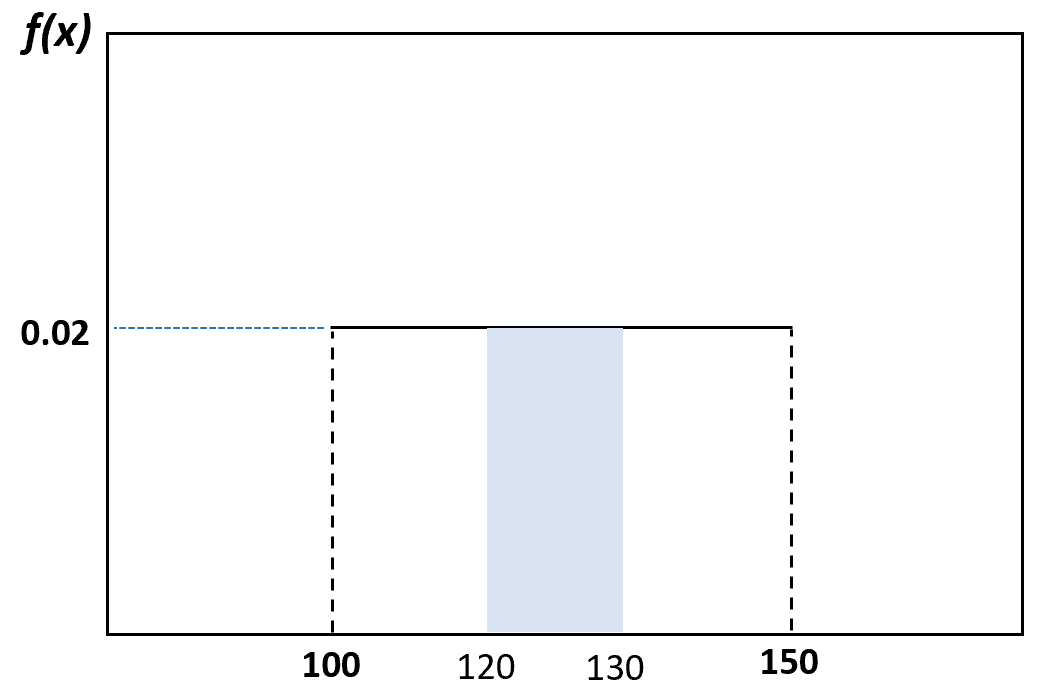
إذا اخترنا دولفينًا عشوائيًا، فيمكننا استخدام الصيغة أعلاه لتحديد احتمال أن يتراوح وزن الدلفين المختار بين 120 و130 رطلاً:

• ف(120 < X < 130) = (130 – 120) / (150 – 100)
• ف(120 < X < 130) = 10/50
• ف(120 < X < 130) = 0.2

احتمال أن يزن الدلفين المختار ما بين 120 و130 رطلاً هو 0.2 .

تصور التوزيع الموحد

إذا قمنا بإنشاء مخطط كثافة لتصور التوزيع الموحد، فسيبدو مثل المخطط التالي:

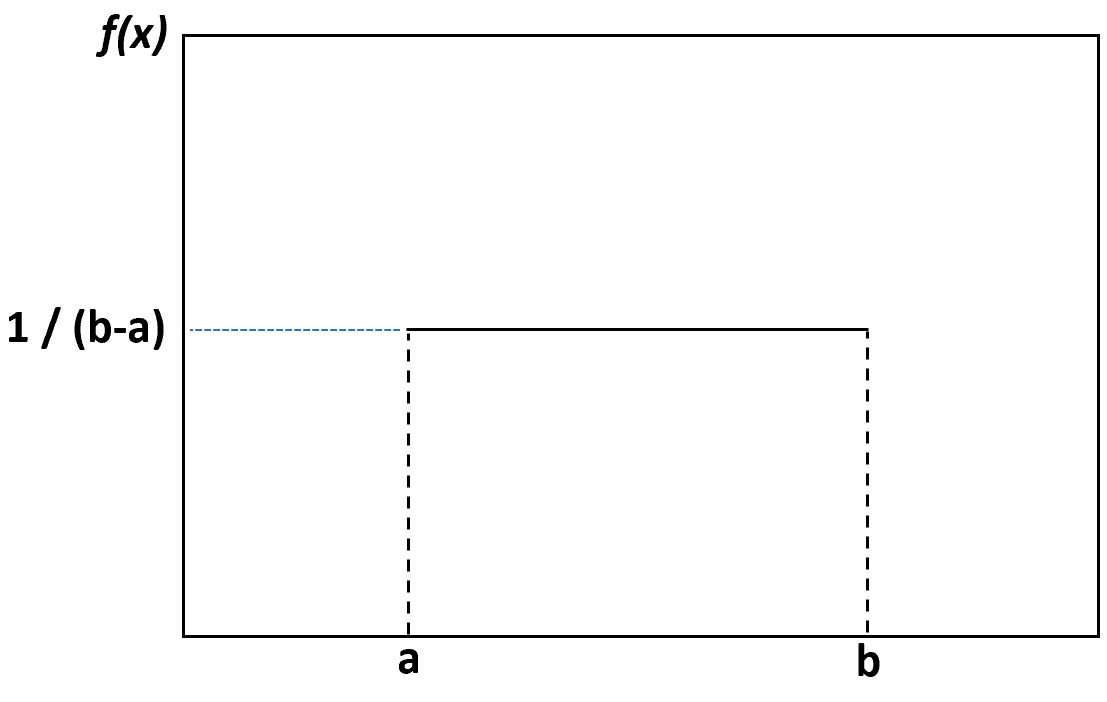
كل قيمة تقع بين الحد الأدنى أ والحد الأعلى ب لها نفس احتمال الحدوث وأي قيمة خارج هذه الحدود يكون احتمال حدوثها صفرًا.

على سبيل المثال، في مثالنا السابق، قلنا أن وزن الدلافين موزع بالتساوي بين 100 و150 رطل. إليك كيفية تصور هذا التوزيع:

ويمكن تصور احتمال أن يزن الدلفين الذي تم اختياره عشوائيًا ما بين 120 و130 رطلًا على النحو التالي:

خصائص التوزيع الموحد

التوزيع الموحد له الخصائص التالية:

• المتوسط: (أ + ب) / 2
• الوسيط: (أ + ب) / 2
• الانحراف المعياري: √ (ب – أ) ² / 12
• الفرق : ( ب – أ ) ² / 12

على سبيل المثال، لنفترض أن وزن الدلافين موزع بالتساوي بين 100 و150 رطلاً.

يمكننا حساب الخصائص التالية لهذا التوزيع:

• متوسط الوزن: (أ + ب) / 2 = (150 + 100) / 2 = 125
• الوزن المتوسط: (أ + ب) / 2 = (150 + 100) / 2 = 125
• الانحراف المعياري للوزن: √ (150 – 100) ² / 12 = 14.43
• اختلاف الوزن : (150 – 100) ² / 12 = 208.33

مشاكل تتعلق بممارسات التوزيع الموحدة

استخدم المسائل التدريبية التالية لاختبار معرفتك بالتوزيع الموحد.

السؤال 1: تصل الحافلة إلى محطة الحافلات كل 20 دقيقة. إذا وصلت إلى محطة الحافلات، ما هو احتمال أن تصل الحافلة خلال 8 دقائق أو أقل؟

الحل 1: الحد الأدنى لوقت الانتظار هو 0 دقيقة والحد الأقصى لوقت الانتظار هو 20 دقيقة. قيمة الفائدة الأقل هي 0 دقيقة وقيمة الفائدة العليا هي 8 دقائق.

لذلك، فإننا سوف نحسب الاحتمال على النحو التالي:

P(0 < X < 8) = (8-0) / (20-0) = 8/20 = 0.4 .

السؤال 2: يتم توزيع مدة مباراة الدوري الاميركي للمحترفين بالتساوي بين 120 و170 دقيقة. ما هو احتمال أن تستمر مباراة NBA التي تم اختيارها عشوائيًا لأكثر من 155 دقيقة؟

الحل 2: الحد الأدنى للمدة هو 120 دقيقة والحد الأقصى للمدة هو 170 دقيقة. قيمة الفائدة الأقل هي 155 دقيقة وقيمة الفائدة العليا هي 170 دقيقة.

لذلك، فإننا سوف نحسب الاحتمال على النحو التالي:

ف(155 < X < 170) = (170-155) / (170-120) = 15/50 = 0.3 .

السؤال 3: وزن نوع معين من الضفادع موزع بالتساوي ما بين 15 إلى 25 جرام. إذا اخترت ضفدعًا عشوائيًا، فما احتمال أن يتراوح وزنه بين 17 و19 جرامًا؟

الحل 3: الحد الأدنى للوزن 15 جرامًا والحد الأقصى للوزن 25 جرامًا. قيمة الفائدة الدنيا هي 17 جرامًا وقيمة الفائدة العليا هي 19 جرامًا.

لذلك، فإننا سوف نحسب الاحتمال على النحو التالي:

ف(17 < X < 19) = (19-17) / (25-15) = 2/10 = 0.2 .

ملاحظة: يمكننا استخدام حاسبة التوزيع الموحد للتحقق من إجاباتنا على كل من هذه المسائل.