ما هو عامل anova؟ (التعريف & #038؛ مثال)

ANOVA العاملي هو أي ANOVA (“تحليل التباين”) يستخدم عاملين مستقلين أو أكثر ومتغير استجابة واحد.

يجب استخدام هذا النوع من ANOVA عندما تريد فهم كيفية تأثير عاملين أو أكثر على متغير الاستجابة وما إذا كان هناك تأثير تفاعل بين العوامل على متغير الاستجابة أم لا.

يقدم هذا البرنامج التعليمي عدة أمثلة للمواقف التي يمكن فيها استخدام تحليل التباين العاملي، بالإضافة إلى مثال خطوة بخطوة لكيفية إجراء تحليل التباين العاملي.

ملحوظة: تحليل التباين ثنائي الاتجاه هو نوع من تحليل التباين العاملي.

أمثلة على استخدام تحليل التباين العاملي

يمكن استخدام ANOVA العاملي في كل من الحالات التالية.

مثال 1: نمو النبات

يريد عالم النبات أن يفهم كيف يؤثر التعرض لأشعة الشمس وتكرار الري على نمو النبات. تقوم بزراعة 100 بذرة وتتركها تنمو لمدة ثلاثة أشهر في ظل ظروف مختلفة من التعرض لأشعة الشمس وتكرار الري. وبعد ثلاثة أشهر، تسجل ارتفاع كل نبات.

وفي هذه الحالة، يحتوي على المتغيرات التالية:

• متغير الاستجابة: نمو النبات
• العوامل: التعرض لأشعة الشمس، وتكرار الري

و تود الإجابة على الأسئلة التالية:

• هل يؤثر التعرض لأشعة الشمس على نمو النبات؟
• هل يؤثر تكرار الري على نمو النبات؟
• هل هناك تأثير تفاعلي بين التعرض لأشعة الشمس وتكرار الري؟

قد تستخدم تحليل التباين (ANOVA) العاملي لهذا التحليل لأنها تريد فهم كيفية تأثير عاملين على متغير استجابة واحد.

مثال 2: نتائج الامتحانات

يريد الأستاذ أن يفهم كيف يؤثر وقت الفصل وطريقة التدريس على نتائج الامتحان. ويستخدم طريقتين مختلفتين للتدريس ووقتين مختلفين للتدريس (في الصباح الباكر وفي وقت مبكر من بعد الظهر) ويسجل متوسط درجات امتحان كل طالب في نهاية الفصل الدراسي.

وفي هذه الحالة يحتوي على المتغيرات التالية:

• متغير الاستجابة: درجة الامتحان
• العوامل: طريقة التدريس، وقت التدريس

و يرغب في الإجابة على الأسئلة التالية:

• هل تؤثر طريقة التدريس على نتائج الامتحانات؟
• هل يؤثر وقت التدريس على درجات الامتحان؟
• هل هناك تأثير تفاعلي بين طريقة التدريس ووقت التدريس؟

قد يستخدم تحليل التباين (ANOVA) العاملي لهذا التحليل لأنه يريد أن يفهم كيفية تأثير عاملين على متغير استجابة واحد.

مثال 3: الدخل السنوي

يقوم خبير اقتصادي بجمع البيانات لفهم كيفية تأثير مستوى التعليم (شهادة الدراسة الثانوية، دبلوم الكلية، درجة الدراسات العليا)، والحالة الاجتماعية (أعزب، مطلق، متزوج)، والمنطقة (الشمال والشرق والجنوب والغرب) على الدخل السنوي.

وفي هذه الحالة يحتوي على المتغيرات التالية:

• متغير الاستجابة: الدخل السنوي
• العوامل: المستوى التعليمي، الحالة الاجتماعية، المنطقة

و يرغب في الإجابة على الأسئلة التالية:

• هل يؤثر المستوى التعليمي على الدخل؟
• هل تؤثر الحالة الاجتماعية على الدخل؟
• هل تؤثر المنطقة على الدخل؟
• هل هناك تأثير تفاعل بين هذه العوامل الثلاثة المستقلة؟

قد يستخدم تحليل التباين (ANOVA) العاملي لهذا التحليل لأنه يريد أن يفهم كيف تؤثر ثلاثة عوامل على متغير استجابة واحد.

مثال خطوة بخطوة لتحليل التباين العاملي

يريد عالم النبات معرفة ما إذا كان التعرض لأشعة الشمس وتكرار الري يؤثر على نمو النبات. تزرع 40 بذرة وتتركها تنمو لمدة شهرين في ظروف مختلفة من التعرض لأشعة الشمس وتكرار الري. وبعد شهرين، تسجل ارتفاع كل نبات.

النتائج موضحة أدناه:

يمكننا أن نرى أنه تم زراعة خمسة نباتات في كل مجموعة من الظروف.

على سبيل المثال، تمت زراعة خمسة نباتات بسقي يومي وبدون ضوء الشمس وكان ارتفاعها بعد شهرين 4.8 بوصة، 4.4 بوصة، 3.2 بوصة، 3.9 بوصة، 4.4 بوصة:

يستخدم عالم النبات هذه البيانات لإجراء تحليل التباين العاملي في Excel ويحصل على النتيجة التالية:

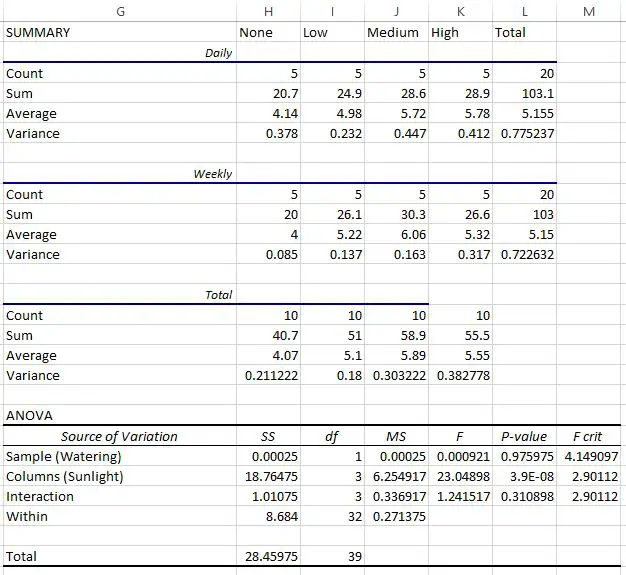
ويبين الجدول الأخير نتيجة تحليل التباين العاملي:

• وكانت القيمة p للتفاعل بين تكرار الري والتعرض للشمس 0.310898 . وهذا ليس ذو دلالة إحصائية عند مستوى 0.05 ألفا.
• وكانت القيمة p لتكرار الري 0.975975 . وهذا ليس ذو دلالة إحصائية عند مستوى 0.05 ألفا.
• كانت القيمة p للتعرض لأشعة الشمس 3.9E-8 (0.000000039) . وهذا ذو دلالة إحصائية عند مستوى ألفا 0.05.

ويمكننا أن نستنتج أن التعرض لأشعة الشمس هو العامل الوحيد الذي له تأثير ذو دلالة إحصائية على نمو النبات.

كما يمكن أن نستنتج أنه لا يوجد أي تأثير تفاعلي بين التعرض للشمس وتكرار الري وأن تكرار الري ليس له تأثير ذو دلالة إحصائية على نمو النبات. النباتات.

مصادر إضافية

توفر البرامج التعليمية التالية معلومات إضافية حول نماذج ANOVA:

مقدمة إلى تحليل التباين الأحادي (One-Way ANOVA).
مقدمة إلى تحليل التباين ثنائي الاتجاه
مقدمة للتدابير المتكررة ANOVA
الاختلافات بين أنوفا، أنكوفا، مانوفا ومانكوفا