ما هو الانحدار المنحني؟ (تعريف وأمثلة)
الانحدار المنحني هو الاسم الذي يطلق على أي نموذج انحدار يحاول ملاءمة المنحنى بدلاً من الخط المستقيم.
تتضمن الأمثلة الشائعة لنماذج الانحدار المنحني ما يلي:
الانحدار التربيعي: يستخدم عند وجود علاقة تربيعية بين متغير متنبئ ومتغير استجابة . عند رسمها بيانيًا، يبدو هذا النوع من العلاقات على شكل حرف “U” أو حرف “U” مقلوب على مخطط التشتت:
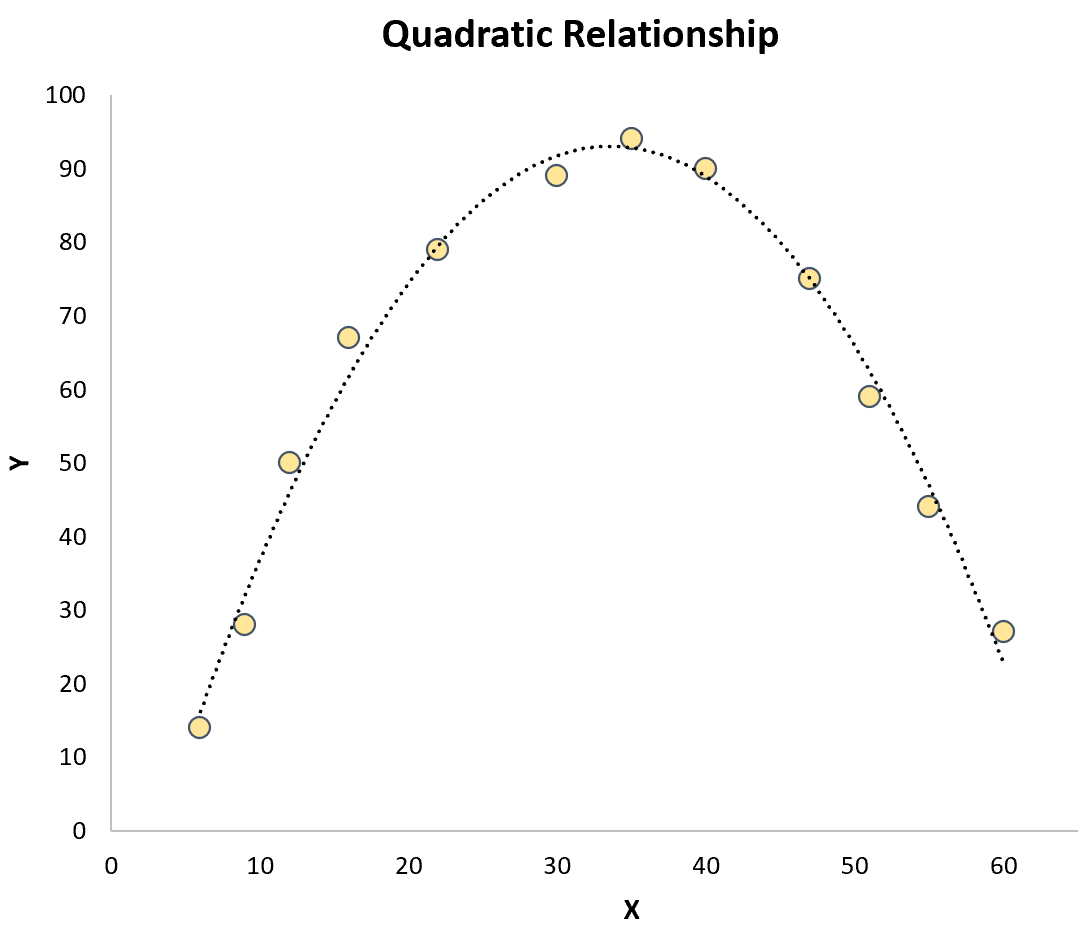
الانحدار المكعب: يستخدم عند وجود علاقة مكعبة بين متغير متنبئ ومتغير استجابة. عند رسمها بيانيًا، يُظهر هذا النوع من العلاقات منحنيين متميزين على مخطط التشتت:
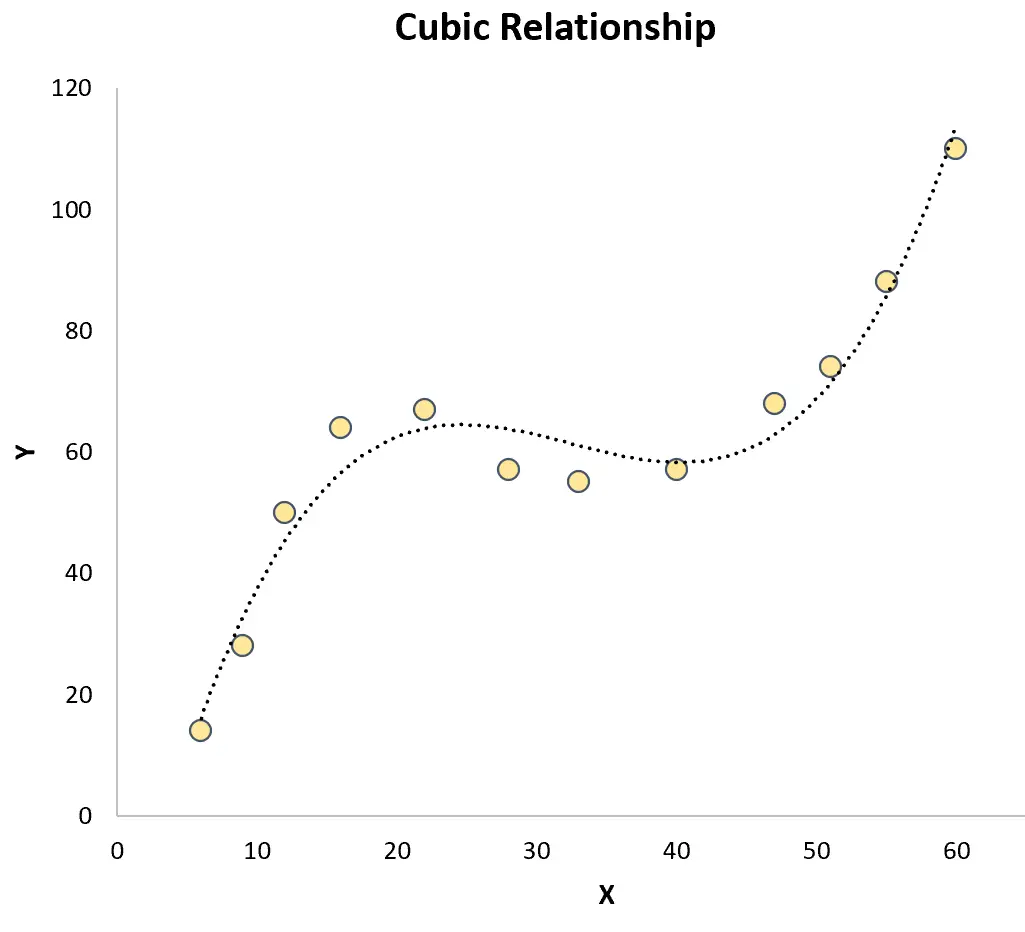
يتناقض كلاهما مع الانحدار الخطي البسيط الذي تكون فيه العلاقة بين متغير التوقع ومتغير الاستجابة خطية:
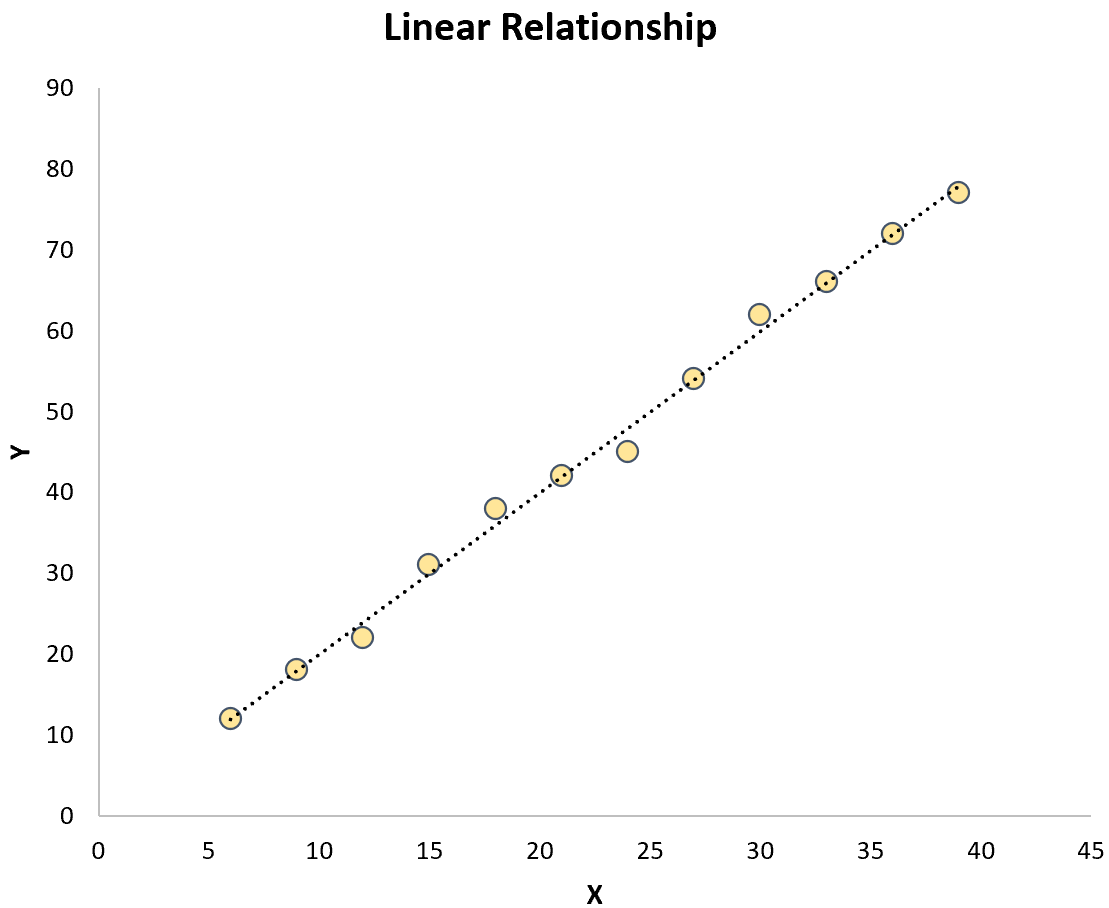
صيغة نماذج الانحدار المنحني
يحاول نموذج الانحدار الخطي البسيط احتواء مجموعة من البيانات باستخدام الصيغة التالية:
ŷ = β 0 + β 1 س
ذهب:
- ŷ: متغير الاستجابة
- β 0 , β 1 : معاملات الانحدار
- x: المتغير التنبؤي
في المقابل، يستخدم نموذج الانحدار التربيعي الصيغة التالية:
ŷ = β 0 + β 1 س + β 2 × 2
ويستخدم نموذج الانحدار المكعب الصيغة التالية:
ŷ = β 0 + β 1 س + β 2 × 2 + β 3 × 3
الاسم الأكثر عمومية لنماذج الانحدار التي تتضمن الأسس هو الانحدار متعدد الحدود ، والذي يأخذ الصيغة التالية:
ŷ = β 0 + β 1 x + β 2 x 2 + … + β k x k
تشير قيمة k إلى درجة كثير الحدود. على الرغم من أن الدرجة يمكن أن تكون أي رقم موجب، إلا أننا نادرًا ما نلائم نماذج الانحدار متعدد الحدود بدرجة أكبر من 3 أو 4.
باستخدام الأسس في صيغة نموذج الانحدار، تكون نماذج الانحدار متعدد الحدود قادرة على ملاءمة المنحنيات مع مجموعات البيانات بدلاً من الخطوط المستقيمة.
متى يتم استخدام الانحدار المنحني
أسهل طريقة لمعرفة ما إذا كان يجب عليك استخدام الانحدار المنحني أم لا هي إنشاء مخطط انتشار لمتغير التوقع ومتغير الاستجابة.
إذا أظهر مخطط التشتت علاقة خطية بين المتغيرين، فمن المحتمل أن يكون الانحدار الخطي البسيط مناسبًا.
ومع ذلك، إذا أظهر مخطط التشتت نمطًا تربيعيًا أو مكعبًا أو أي نمط منحني آخر بين المتنبئ ومتغير الاستجابة، فمن المحتمل أن يكون الانحدار المنحني أكثر ملاءمة للاستخدام.
يمكنك أيضًا ملاءمة نموذج الانحدار الخطي البسيط ونموذج الانحدار المنحني ومقارنة قيم R-squared المجهزة لكل نموذج لتحديد النموذج الذي يوفر أفضل ملاءمة للبيانات.
يعد R-squared المعدل مفيدًا لأنه يخبرك بمقدار التباين في متغير الاستجابة الذي يمكن تفسيره بواسطة متغير (متغيرات) التوقع، والذي تم ضبطه ليناسب عدد متغيرات التوقع في النموذج.
بشكل عام، يوفر النموذج ذو أعلى قيمة R-squared المعدلة ملاءمة أفضل لمجموعة البيانات.
مصادر إضافية
تشرح البرامج التعليمية التالية كيفية إجراء الانحدار متعدد الحدود في برامج إحصائية مختلفة:
مقدمة للانحدار متعدد الحدود
كيفية تنفيذ الانحدار متعدد الحدود في إكسيل
كيفية إجراء الانحدار متعدد الحدود في بايثون
كيفية إجراء الانحدار متعدد الحدود في R