كيفية إجراء اختبار جزئي f في excel
يتم استخدام اختبار F الجزئي لتحديد ما إذا كان هناك فرق ذو دلالة إحصائية بين نموذج الانحدار والنسخة المتداخلة من نفس النموذج أم لا.
النموذج المتداخل هو ببساطة نموذج يحتوي على مجموعة فرعية من متغيرات التوقع في نموذج الانحدار الشامل.
على سبيل المثال، لنفترض أن لدينا نموذج الانحدار التالي مع أربعة متغيرات متوقعة:
Y = β 0 + β 1 × 1 + β 2 × 2 + β 3 × 3 + β 4 × 4 + ε
مثال على النموذج المتداخل هو النموذج التالي الذي يحتوي على اثنين فقط من متغيرات التوقع الأصلية:
Y = β 0 + β 1 × 1 + β 2 × 2 + ε
لتحديد ما إذا كان هذان النموذجان مختلفان بشكل كبير، يمكننا إجراء اختبار F جزئي، والذي يحسب إحصائية اختبار F التالية:
F = (( RSS مخفض – RSS كامل )/p) / ( RSS كامل /nk)
ذهب:
- RSS المخفض : المجموع المتبقي لمربعات النموذج المخفض (أي “المتداخل”).
- RSS كامل : المجموع المتبقي لمربعات النموذج الكامل.
- p: عدد المتنبئين الذين تمت إزالتهم من النموذج الكامل.
- n: إجمالي عدد الملاحظات في مجموعة البيانات.
- ك: عدد المعاملات (بما في ذلك التقاطع) في النموذج الكامل.
يستخدم هذا الاختبارالفرضيات الصفرية والبديلة التالية:
H 0 : جميع المعاملات المحذوفة من النموذج الكامل هي صفر.
HA A : واحد على الأقل من المعاملات التي تمت إزالتها من النموذج الكامل غير صفر.
إذا كانت القيمة p المقابلة لإحصائيات اختبار F أقل من مستوى معين من الأهمية (على سبيل المثال 0.05)، فيمكننا رفض فرضية العدم ونستنتج أن واحدًا على الأقل من المعاملات التي تمت إزالتها من النموذج الكامل مهم.
يوضح المثال التالي كيفية إجراء اختبار F جزئي في Excel.
مثال: اختبار جزئي F في Excel
لنفترض أن لدينا مجموعة البيانات التالية في Excel:
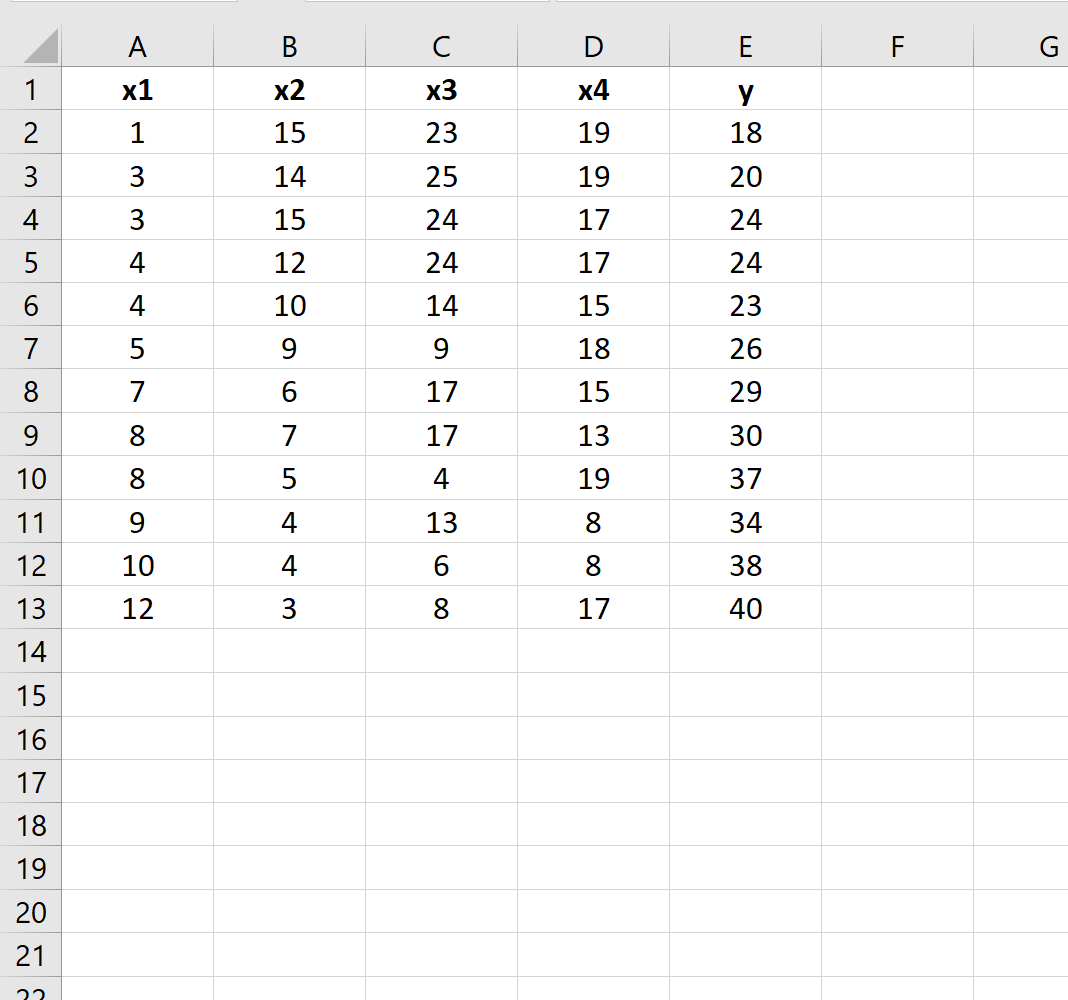
لنفترض أننا نريد تحديد ما إذا كان هناك فرق بين نموذجي الانحدار التاليين:
النموذج الكامل: y = β 0 + β 1 x 1 + β 2 x 2 + β 3 x 3 + β 4 x 4
النموذج المخفض: y = β 0 + β 1 x 1 + β 2 x 2
يمكننا إجراء انحدار خطي متعدد في برنامج Excel لكل نموذج للحصول على النتيجة التالية:
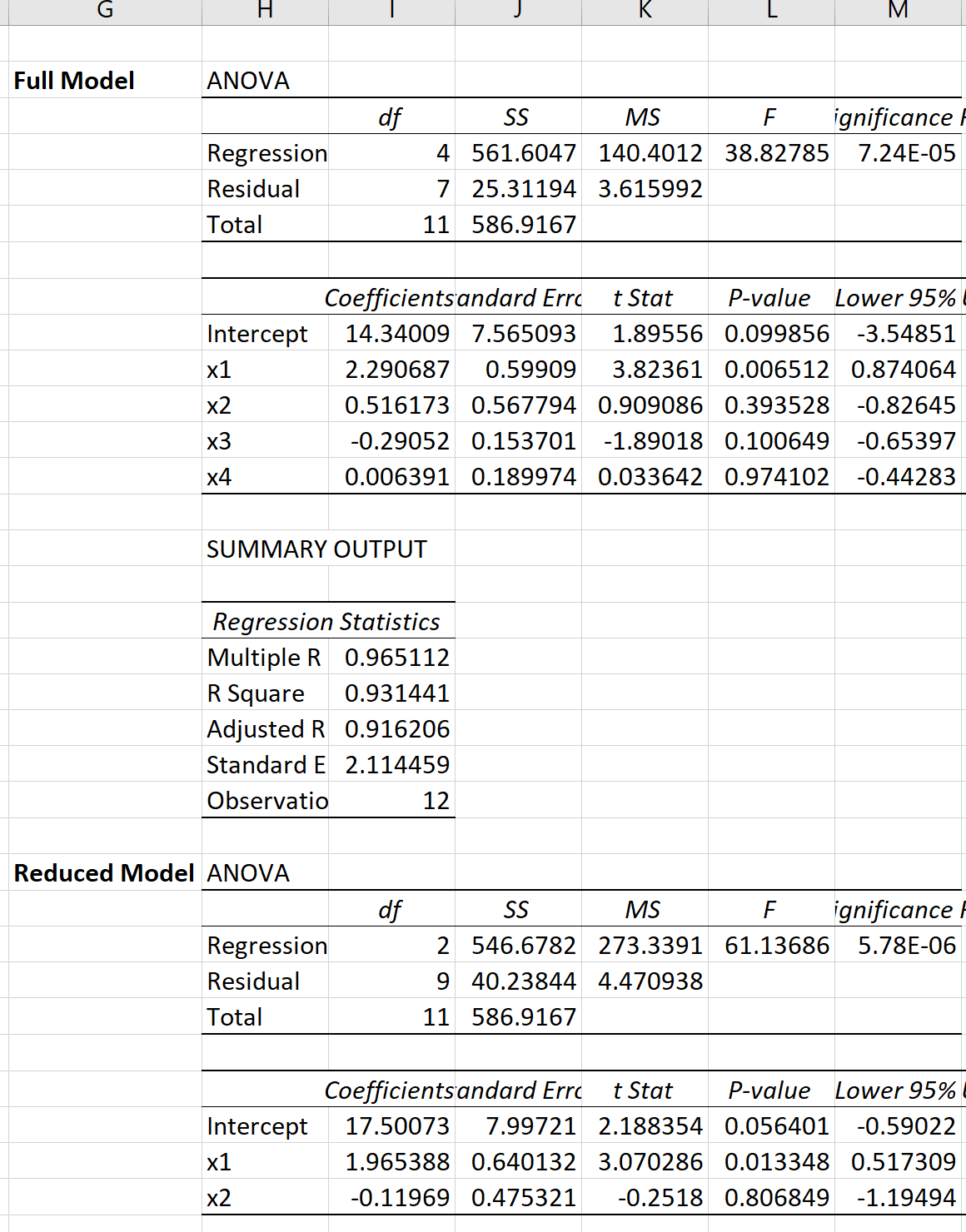
يمكننا بعد ذلك استخدام الصيغة التالية لحساب إحصائيات اختبار F للاختبار الجزئي F:
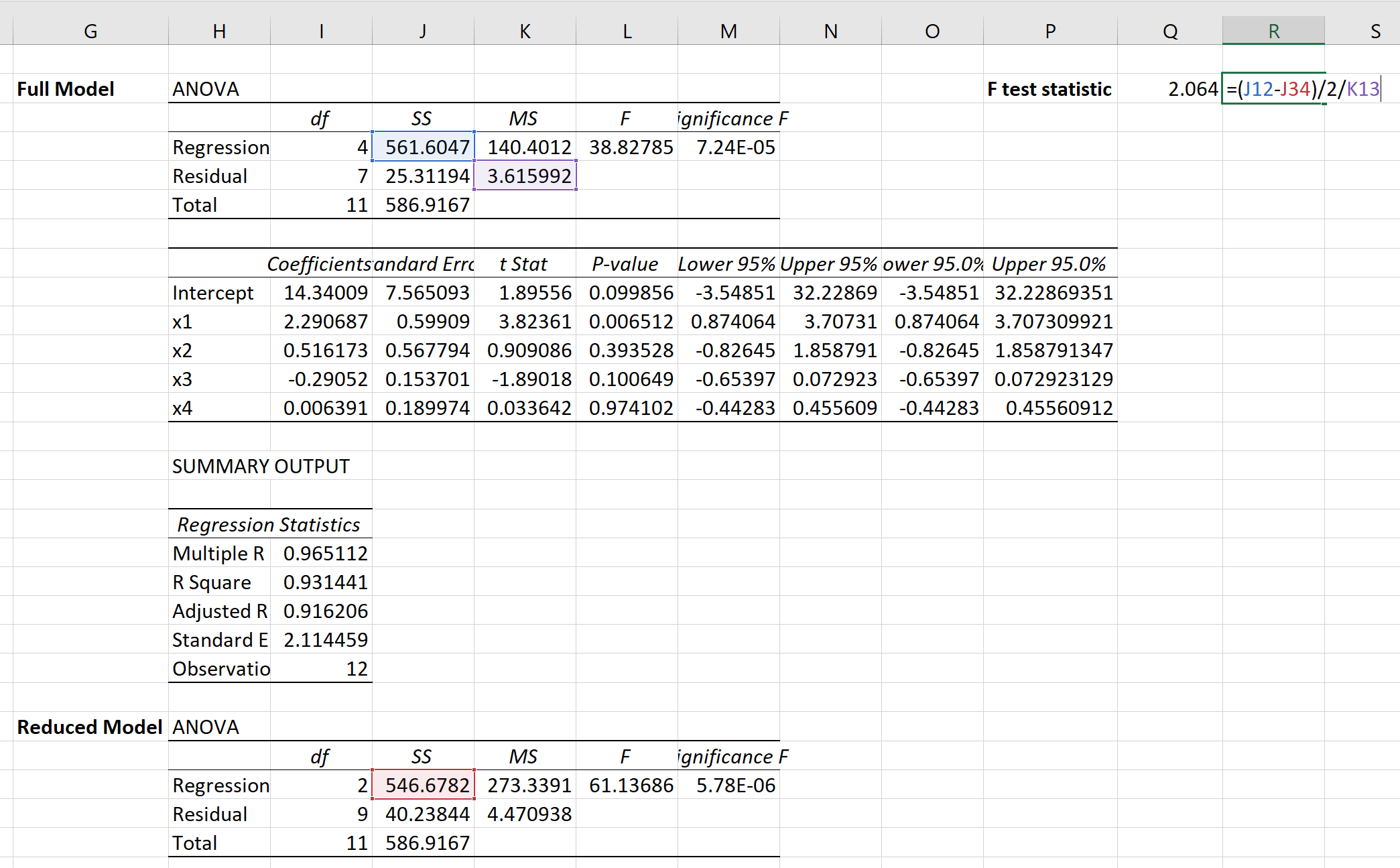
وتبين أن إحصائيات الاختبار هي 2.064 .
يمكننا بعد ذلك استخدام الصيغة التالية لحساب القيمة الاحتمالية المقابلة:
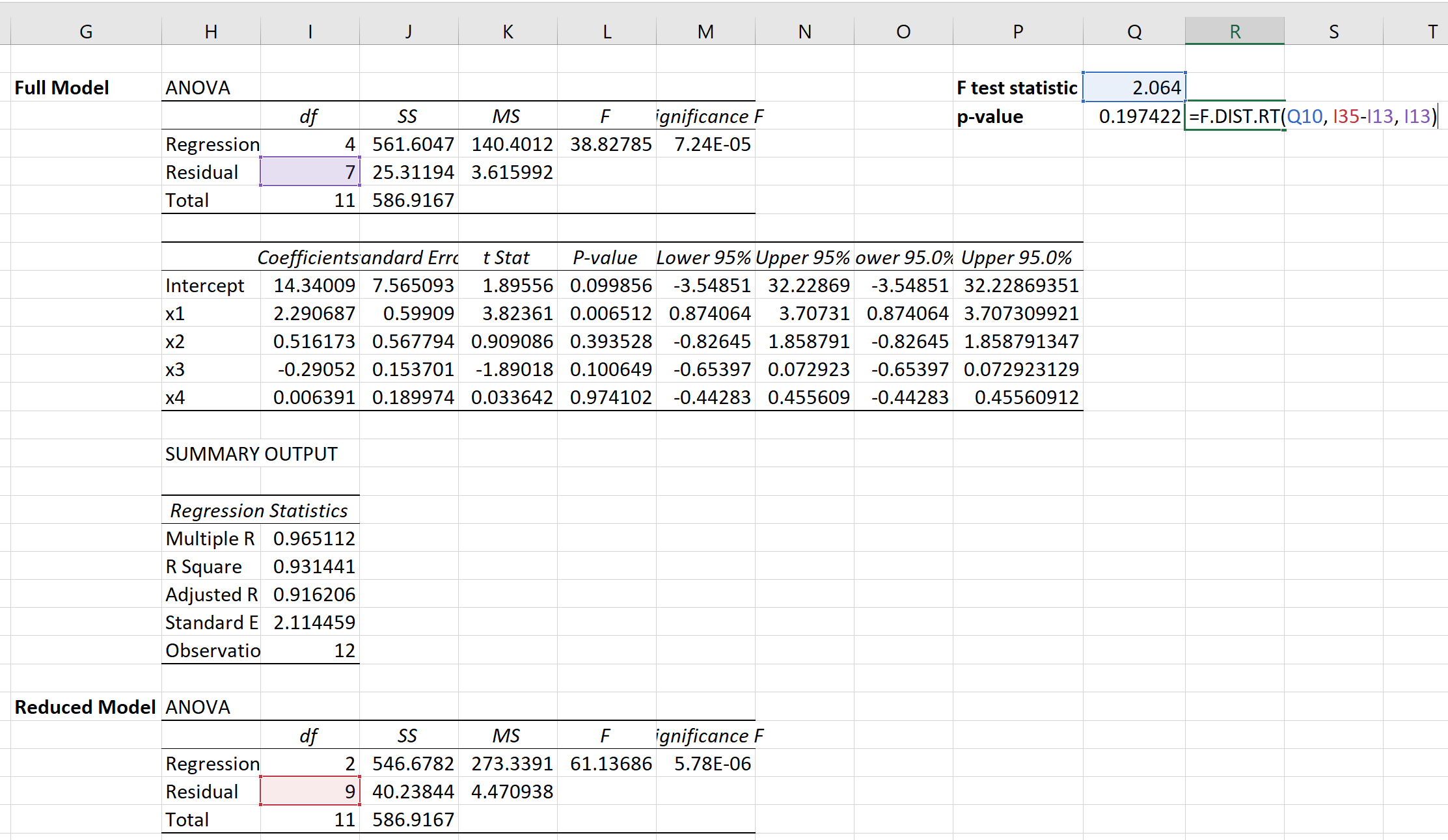
وتبين أن القيمة p هي 0.1974 .
وبما أن هذه القيمة p لا تقل عن 0.05، فسوف نفشل في رفض فرضية العدم. وهذا يعني أنه ليس لدينا ما يكفي من الأدلة لنقول أن أيًا من متغيرات التوقع x3 أو x4 له دلالة إحصائية.
بمعنى آخر، إضافة x3 و x4 إلى نموذج الانحدار لا يؤدي إلى تحسين ملاءمة النموذج بشكل ملحوظ.
مصادر إضافية
كيفية تنفيذ الانحدار الخطي البسيط في إكسيل
كيفية إجراء الانحدار الخطي المتعدد في إكسيل
كيفية حساب الخطأ القياسي للانحدار في إكسيل
About Author
دكتور بنيامين أندرسون
مرحبًا، أنا بنجامين، أستاذ الإحصاء المتقاعد الذي تحول إلى مدرس متخصص في Statorials. بفضل خبرتي الواسعة في مجال الإحصاء، فأنا حريص على مشاركة معرفتي لتمكين الطلاب من خلال Statorials. تعرف أكثر