Binompdf مقابل binomcdf: الفرق (بالإضافة إلى أمثلة)

يعد التوزيع ذو الحدين أحد التوزيعات الأكثر استخدامًا في جميع الإحصائيات.

في الآلة الحاسبة TI-84، يمكنك استخدام وظيفتين للعثور على الاحتمالات المتعلقة بالتوزيع ذي الحدين:

• binompdf(n, p, x) : يبحث عن احتمال حدوث نجاحات x بالضبط على مدار تجارب n حيث يكون احتمال النجاح في تجربة معينة يساوي p .
• binomcdf(n, p, x) : يبحث عن احتمال حدوث نجاح x أو أقل خلال تجارب n حيث يكون احتمال النجاح في تجربة معينة يساوي p .

يمكنك الوصول إلى كل من هذه الوظائف على الآلة الحاسبة TI-84 بالضغط على 2nd ثم الضغط على VARS . سينقلك هذا إلى شاشة DISTR حيث يمكنك بعد ذلك استخدام binompdf() و binomcdf() :

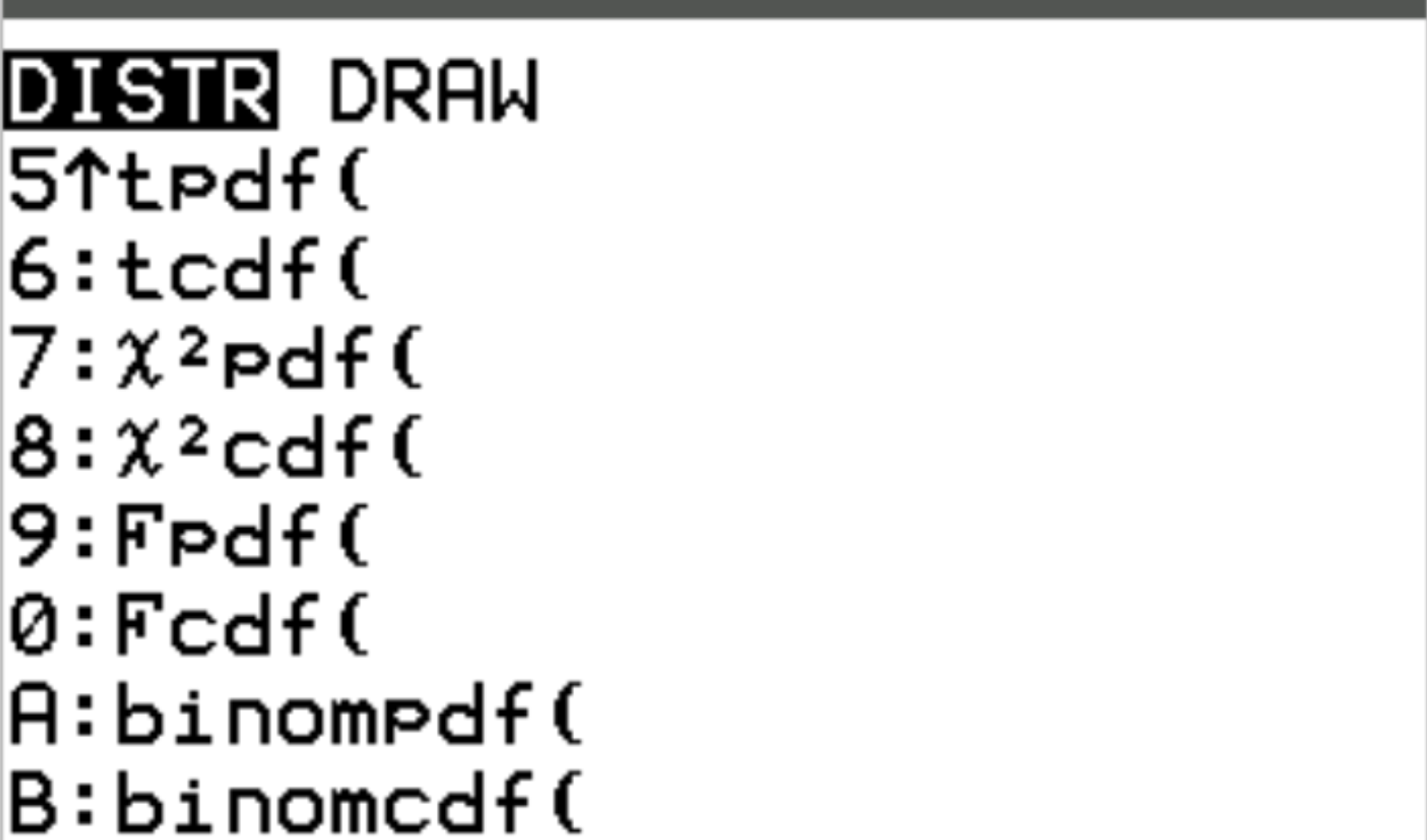
توضح الأمثلة التالية كيفية استخدام كل من هذه الوظائف عمليًا.

أمثلة: كيفية استخدام Binompdf()

توضح الأمثلة التالية كيفية استخدام الدالة binompdf() .

مثال 1: محاولات الرمية الحرة

تقوم جيسيكا بـ 80% من محاولات الرمية الحرة. إذا نفذت ١٠ رميات حرة، فما احتمال أن تنفذ ٧ رميات بالضبط؟

للإجابة على هذا السؤال يمكننا كتابة الصيغة التالية:

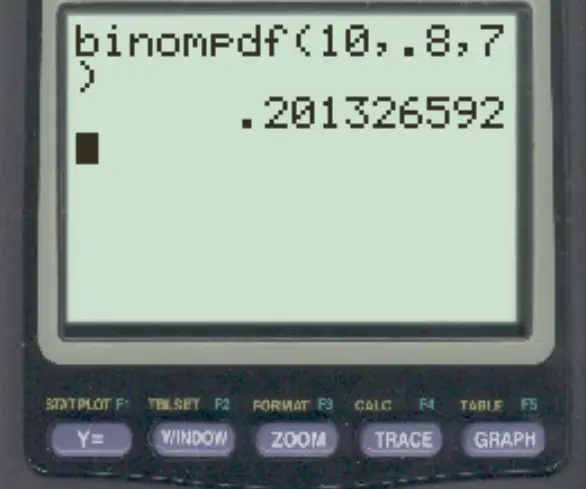
احتمال حصولها على 7 بالضبط هو 0.2013 .

مثال 2: المعاملات الاحتيالية

يعلم البنك أن 3% من جميع المعاملات تكون احتيالية. إذا حدثت 20 معاملة في يوم معين، ما هو احتمال أن تكون اثنتان بالضبط احتياليتين؟

للإجابة على هذا السؤال يمكننا كتابة الصيغة التالية:

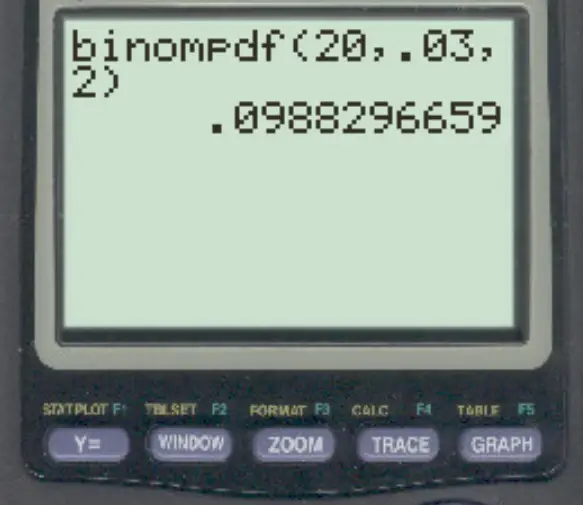
احتمال أن تكون معاملتان احتياليتان بالضبط هو 0.0988 .

أمثلة: كيفية استخدام Binomcdf()

توضح الأمثلة التالية كيفية استخدام الدالة binomcdf() .

مثال 1: محاولات الرمية الحرة

تقوم جيسيكا بـ 50% من محاولات الرمية الحرة. إذا نفذت ١٠ رميات حرة، فما احتمال أن تقوم بسبع رميات أو أقل؟

للإجابة على هذا السؤال يمكننا كتابة الصيغة التالية:

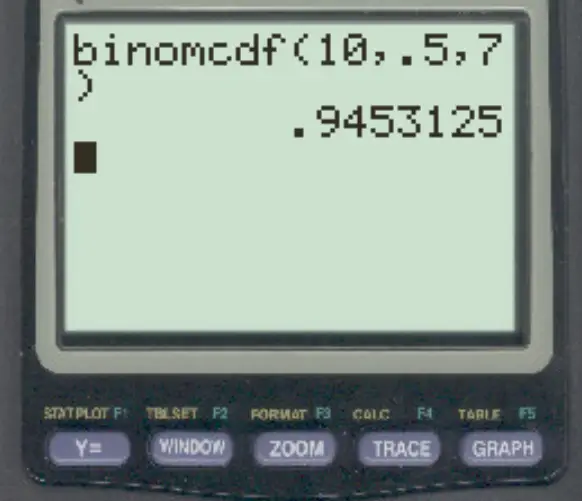
احتمال قيامها بـ 7 رميات حرة أو أقل هو 0.9453 .

مثال 2: المعاملات الاحتيالية

يعلم البنك أن 3% من جميع المعاملات تكون احتيالية. إذا حدثت 20 معاملة في يوم معين، ما هو احتمال أن تكون أكثر من معاملتين احتياليتين؟

للإجابة على هذا السؤال يمكننا كتابة الصيغة التالية:

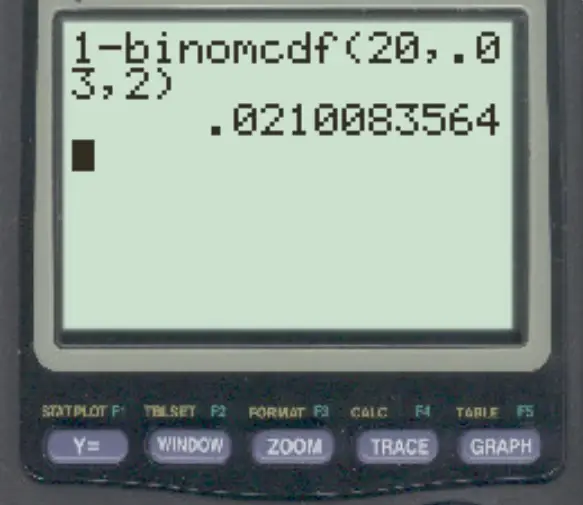
احتمال أن تكون أكثر من معاملتين احتياليتين هو 0.021 .

مصادر إضافية

حاسبة التوزيع ذات الحدين
كيفية إجراء اختبار ذي الحدين في إكسيل