الدليل الكامل: كيفية التحقق من افتراضات manova

يتم استخدام MANOVA (تحليل التباين متعدد المتغيرات) لتحليل كيفية تأثير متغير عامل واحد أو أكثر على متغيرات الاستجابة المتعددة.

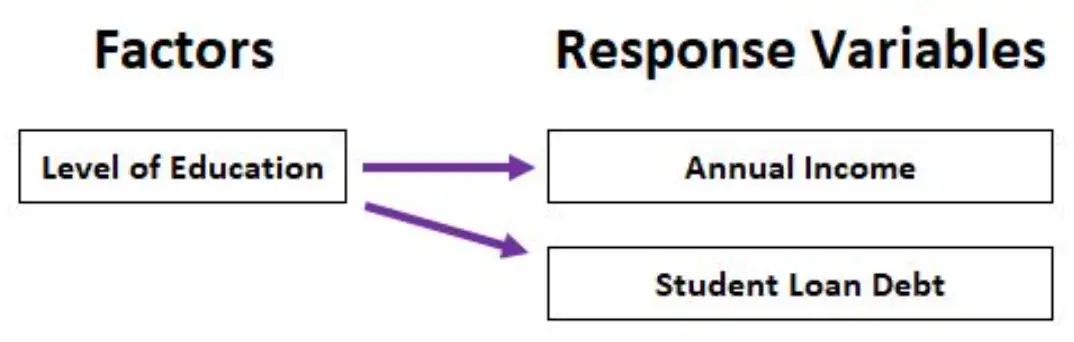
على سبيل المثال، يمكننا استخدام MANOVA لتحليل كيفية تأثير مستوى التعليم (شهادة الدراسة الثانوية، درجة الزمالة، درجة البكالوريوس، درجة الماجستير) على كل من الدخل السنوي وإجمالي ديون القروض الطلابية.

ذات صلة: الاختلافات بين ANOVA وANCOVA وMANOVA وMANCOVA

في كل مرة نقوم فيها بإجراء تحليل MANOVA، يجب علينا التحقق من استيفاء الافتراضات التالية:

1. الحالة الطبيعية متعددة المتغيرات – متغيرات الاستجابة متعددة المتغيرات موزعة بشكل طبيعي داخل كل مجموعة من متغيرات العامل.

2. الاستقلال – يتم أخذ كل ملاحظة بشكل عشوائي ومستقل من السكان.

3. التباين المتساوي – مصفوفات التباين السكاني لكل مجموعة متساوية.

4. لا توجد قيم متطرفة متعددة المتغيرات – لا توجد قيم متطرفة متعددة المتغيرات.

وفي هذه المقالة نقدم شرحًا لكل افتراض بالإضافة إلى كيفية تحديد ما إذا كان الافتراض قد تحقق أم لا.

الافتراض 1: الحالة الطبيعية متعددة المتغيرات

يفترض MANOVA أن متغيرات الاستجابة متعددة المتغيرات موزعة بشكل طبيعي داخل كل مجموعة من متغير العامل.

إذا كان هناك ما لا يقل عن 20 ملاحظة لكل عامل * مجموعة متغيرات الاستجابة، فيمكننا أن نفترض أن افتراض الحالة الطبيعية متعددة المتغيرات قد تم استيفائه.

إذا كان هناك أقل من 20 ملاحظة لكل مجموعة متغيرات العامل*الاستجابة، فيمكننا إنشاء مصفوفة مخطط التشتت لتصور البقايا والتحقق بصريًا من استيفاء هذا الافتراض.

لحسن الحظ، من المعروف أن MANOVA مقاوم للانحرافات عن الوضع الطبيعي متعدد المتغيرات، لذا فإن الانحرافات الصغيرة إلى المتوسطة لا تمثل مشكلة بشكل عام.

الفرضية 2: الاستقلال

تفترض MANOVA أن كل ملاحظة يتم أخذ عينات منها بشكل عشوائي ومستقل من السكان.

طالما يتم استخدام طريقة أخذ العينات الاحتمالية (كل فرد في المجتمع لديه احتمالية متساوية لاختياره ليكون في العينة) لجمع البيانات، يمكننا أن نفترض أنه تم أخذ عينات من كل ملاحظة بطريقة عشوائية ومستقلة.

تتضمن أمثلة طرق أخذ العينات الاحتمالية ما يلي:

• عينة عشوائية بسيطة
• اخذ عينة عشوائية
• أخذ العينات العنقودية العشوائية
• أخذ العينات العشوائية المنهجية

الافتراض 3: التباين المتساوي

تفترض MANOVA أن مصفوفات التغاير السكاني لكل مجموعة متساوية.

الطريقة الأكثر شيوعًا لاختبار هذه الفرضية هي استخدام اختبار Box’s M. من المعروف أن هذا الاختبار صارم تمامًا، ولهذا السبب نستخدم عمومًا مستوى أهمية قدره 0.001 لتحديد ما إذا كانت مصفوفات التغاير السكاني متساوية أم لا.

إذا كانت القيمة الاحتمالية لاختبار Box’s M أكبر من 0.001، فيمكننا أن نفترض أن هذا الافتراض قد تحقق.

ولحسن الحظ، حتى لو كانت القيمة الاحتمالية للاختبار أقل من 0.001، فإن MANOVA يميل إلى أن يكون قويًا في مواجهة الانحرافات عن هذه الفرضية.

لكي تكون مصفوفات التغاير غير المتساوية مشكلة، يجب أن تكون الاختلافات بين مصفوفات التغاير كبيرة جدًا.

الفرضية 4: لا توجد قيم متطرفة متعددة المتغيرات

تفترض MANOVA عدم وجود قيم متطرفة متعددة المتغيرات في البيانات والتي يمكن أن تؤثر بشكل كبير على النتائج.

الطريقة الأكثر شيوعًا للتحقق من هذا الافتراض هي حساب مسافة ماهالانوبيس لكل ملاحظة، والتي تمثل المسافة بين نقطتين في مساحة متعددة المتغيرات.

إذا كانت القيمة p المقابلة لمسافة ماهالانوبيس للملاحظة أقل من 0.001، فإننا نعلن عمومًا أن هذه الملاحظة تعتبر قيمة متطرفة.

ارجع إلى البرامج التعليمية التالية لمعرفة كيفية حساب مسافة المهالانوبيس في البرامج الإحصائية المختلفة:

• كيفية حساب مسافة Mahalanobis في R
• كيفية حساب مسافة المهالانوبيس في برنامج SPSS
• كيفية حساب المسافة Mahalanobis في بايثون

مصادر إضافية

تشرح البرامج التعليمية التالية كيفية إجراء تحليل MANOVA في برامج إحصائية مختلفة:

كيفية إجراء MANOVA في R
كيفية إجراء MANOVA في SPSS
كيفية إجراء مانوفا في ستاتا