دليل كامل: التصميم العاملي 2×3

التصميم العاملي 2 × 3 هو نوع من التصميم التجريبي الذي يسمح للباحثين بفهم تأثيرات متغيرين مستقلين على متغير تابع واحد.

في هذا النوع من التصميم، يكون لمتغير مستقل واحد مستويين والمتغير المستقل الآخر له ثلاثة مستويات.

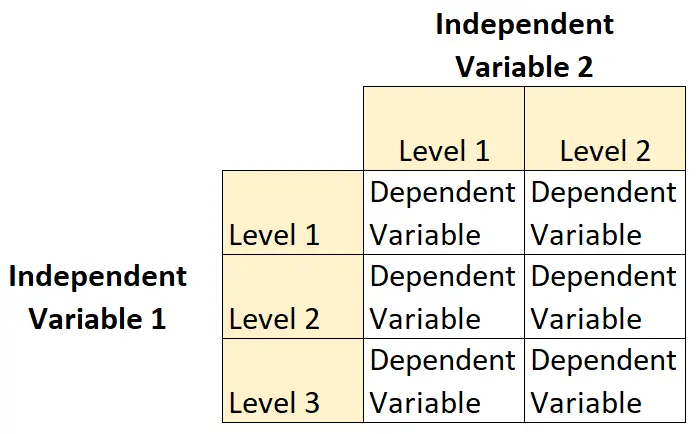
على سبيل المثال، لنفترض أن عالم النبات يريد فهم تأثيرات ضوء الشمس (منخفض أو متوسط أو مرتفع) وتكرار الري (يوميًا أو أسبوعيًا) على نمو نوع نباتي معين.

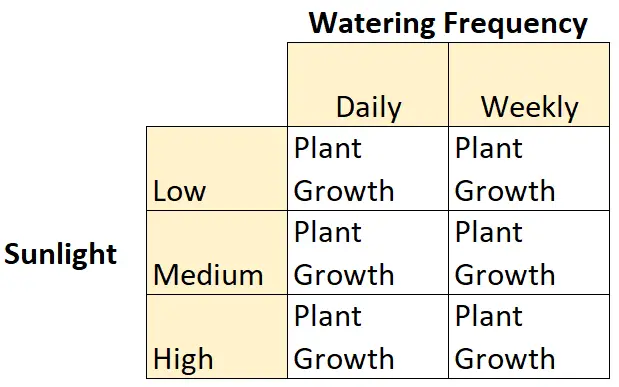
هذا مثال على التصميم العاملي 2 × 3 لأن هناك متغيرين مستقلين، أحدهما بمستويين والآخر بثلاثة مستويات:

• المتغير المستقل رقم 1: ضوء الشمس
  • المستويات: منخفض، متوسط، مرتفع
• المتغير المستقل رقم 2: تكرار الري
  • المستويات: يومي، أسبوعي

وهناك متغير تابع: نمو النبات.

الغرض من التصميم العاملي 2 × 3

يتيح لك التصميم العاملي 2×3 تحليل التأثيرات التالية:

التأثيرات الرئيسية: هي التأثيرات التي يحدثها متغير مستقل واحد على المتغير التابع.

على سبيل المثال، في السيناريو السابق، يمكننا تحليل التأثيرات الرئيسية التالية:

• التأثير الرئيسي لأشعة الشمس على نمو النبات.
  • متوسط نمو جميع النباتات التي تلقت ضوء الشمس المنخفض.
  • متوسط نمو جميع النباتات التي تتلقى ضوء الشمس المتوسط.
  • متوسط نمو جميع النباتات التي تتلقى ضوء الشمس العالي.
• التأثير الرئيسي لتكرار الري على نمو النبات.
  • متوسط نمو جميع النباتات تسقى يوميا.
  • متوسط نمو جميع النباتات تسقى كل أسبوع.

تأثيرات التفاعل: تحدث عندما يعتمد تأثير متغير مستقل على المتغير التابع على مستوى المتغير المستقل الآخر.

على سبيل المثال، في السيناريو السابق، يمكننا تحليل تأثيرات التفاعل التالية:

• هل يعتمد تأثير ضوء الشمس على نمو النبات على عدد مرات الري؟
• هل تأثير تكرار الري على نمو النبات يعتمد على ضوء الشمس؟

كيفية تحليل التصميم العاملي 2 × 3

يمكننا إجراء ANOVA ثنائي الاتجاه لاختبار ما إذا كانت المتغيرات المستقلة لها علاقة ذات دلالة إحصائية مع المتغير التابع أم لا.

على سبيل المثال، يوضح التعليمة البرمجية التالية كيفية إجراء ANOVA ثنائي الاتجاه لسيناريو المصنع الافتراضي الخاص بنا في R:

 #make this example reproducible
set. seeds (0)

#createdata
df <- data. frame (sunlight = rep(c(' Low ', ' Medium ', ' High '), each = 15, times = 2),
                 water = rep(c(' Daily ', ' Weekly '), each = 45, times = 2),
                 growth = c(rnorm(15, 9, 2), rnorm(15, 10, 3), rnorm(15, 13, 2),
                            rnorm(15, 8, 3), rnorm(15, 10, 4), rnorm(15, 12, 3)))

#fit the two-way ANOVA model
model <- aov(growth ~ sunlight * water, data = df)

#view the model output
summary(model)

                Df Sum Sq Mean Sq F value Pr(>F)    
sunlight 2 602.3 301.15 50.811 <2e-16 ***
water 1 39.6 39.62 6.685 0.0105 *  
sunlight:water 2 15.1 7.56 1.275 0.2819    
Residuals 174 1031.3 5.93                   
---
Significant. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

إليك كيفية تفسير نتيجة ANOVA:

• القيمة p المرتبطة بأشعة الشمس هي <2e-16 . وبما أن هذا الرقم أقل من 0.05، فهذا يعني أن التعرض لأشعة الشمس له تأثير ذو دلالة إحصائية على نمو النبات.
• القيمة p المرتبطة بالماء هي 0.0105 . وبما أن هذا الرقم أقل من 0.05، فهذا يعني أن تكرار الري له أيضًا تأثير ذو دلالة إحصائية على نمو النبات.
• القيمة p للتفاعل بين ضوء الشمس والماء هي 0.2819 . وبما أن هذا الرقم لا يقل عن 0.05، فهذا يعني أنه لا يوجد تأثير تفاعل بين ضوء الشمس والماء.

مصادر إضافية

توفر البرامج التعليمية التالية معلومات إضافية حول التصميم التجريبي والتحليل:

الدليل الكامل: التصميم العاملي 2 × 2
ما هي مستويات المتغير المستقل؟
المتغيرات المستقلة أو التابعة
ما هو عامل ANOVA؟