توزيع جاما

By زومار 3, 2023 احتمالا 0 Comments

تشرح هذه المقالة ما هو توزيع جاما وفيم يتم استخدامه. وهكذا ستجد تعريف توزيع جاما وخصائصه وكيف يبدو تمثيله البياني.

ما هو توزيع جاما؟

توزيع جاما هو توزيع احتمالي مستمر يحدده معلمتان مميزتان، α و lect. بمعنى آخر، يعتمد توزيع جاما على قيمة معلمتيه: α هي معلمة الشكل و lect هي معلمة المقياس.

رمز توزيع جاما هو الحرف اليوناني الكبير Γ. لذلك، إذا كان المتغير العشوائي يتبع توزيع جاما، فإنه يكتب على النحو التالي:

X\sim \Gamma(\alpha,\lambda)

يمكن أيضًا تحديد معلمات توزيع جاما باستخدام معلمة الشكل k = α ومعلمة المقياس العكسي θ = 1/α. وفي جميع الحالات، فإن المعلمتين اللتين تحددان توزيع جاما هما أرقام حقيقية موجبة.

عادةً، يتم استخدام توزيع جاما لنمذجة مجموعات البيانات المنحرفة نحو اليمين، بحيث يكون هناك تركيز أكبر للبيانات على الجانب الأيسر من الرسم البياني. على سبيل المثال، يتم استخدام توزيع جاما لنمذجة موثوقية المكونات الكهربائية.

مخطط توزيع جاما

يعتمد الرسم البياني لتوزيع جاما على قيم معلماته المميزة. يمكنك أدناه رؤية كيف تختلف وظيفة الكثافة لتوزيع جاما اعتمادًا على معلمة الشكل ومعلمة المقياس.

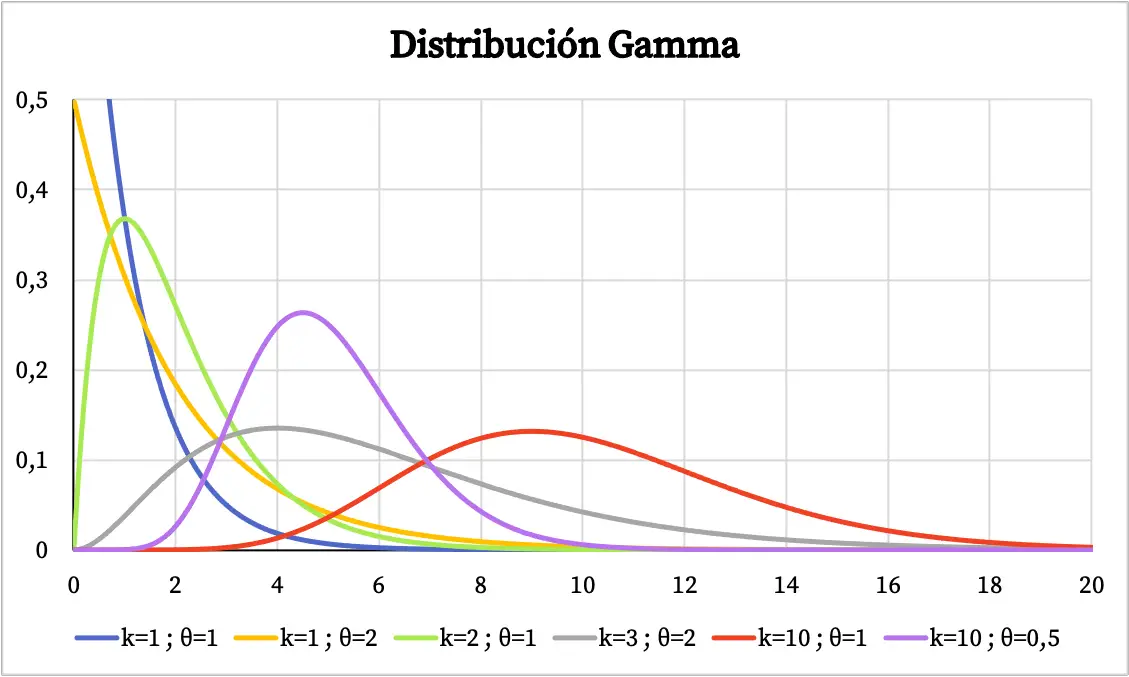
مخطط توزيع جاما

من ناحية أخرى، يمكنك رؤية الرسم البياني لدالة الاحتمالية التراكمية لتوزيع جاما أدناه:

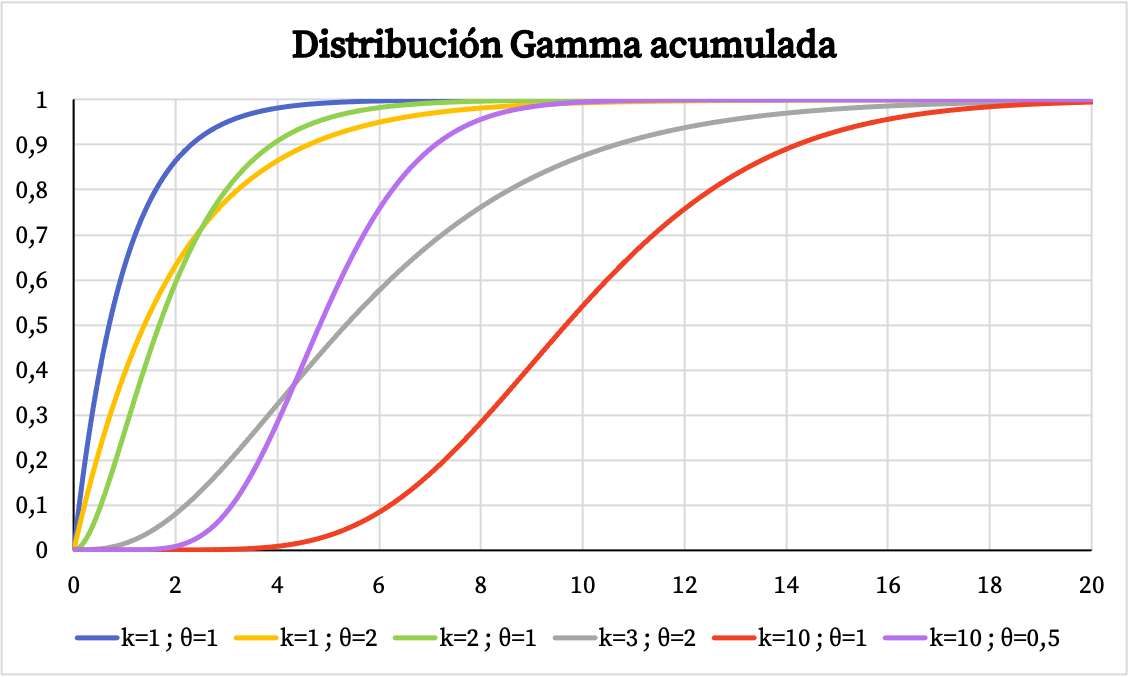
رسم بياني لدالة الاحتمالية التراكمية لتوزيع Gamm

خصائص توزيع جاما

سنرى بعد ذلك ما هي خصائص توزيع جاما.

  • يتم تعريف الرسم البياني لتوزيع جاما بالكامل من خلال المعلمتين المميزتين: α هي معلمة الشكل و lect هي معلمة المقياس.

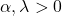
\alpha , \lambda >0″ title=”Rendered by QuickLaTeX.com” height=”16″ width=”62″ style=”vertical-align: -4px;”></p> </p> <ul style=

  • يتكون مجال توزيع جاما من أرقام موجبة فقط.

    • x\in (0,+\infty)

    • متوسط توزيع جاما يساوي النسبة بين معلمة الشكل ومعلمة المقياس، أي α/α.

    E[X]=\cfrac{\alpha}{\lambda}

    • إن تباين توزيع جاما يعادل معلمة الشكل مقسومة على مربع معلمة المقياس.

    Var(X)=\cfrac{\alpha}{\lambda^2}

    • بالنسبة لقيم α أقل من 1، يكون الوضع 0. ولكن إذا كانت α تساوي أو أكبر من 1، فيمكن حساب وضع توزيع جاما بالصيغة التالية:

    \begin{array}{c}Mo=0 \qquad \text{para } \alpha<1\\[2ex]Mo=\cfrac{\alpha-1}{\lambda} \qquad \text{para } \alpha\geq1\end{array}

    • صيغة دالة الكثافة لتوزيع جاما هي:

    \displaystyle f(x)=\frac{\lambda(\lambda x)^{\alpha-1}e^{-\lambda x}}{\Gamma(\alpha)}

    حيث Γ هي دالة جاما، والتي يتم تعريفها على النحو التالي:

    \displaystyle \Gamma(\alpha)=\int_0^\infty t^{\alpha-1}e^{-t}dt

    • صيغة التوزيع التراكمي لمتغير عشوائي محدد بواسطة توزيع جاما هي كما يلي:

    \displaystyle F(x)=\int_0^x\frac{\lambda(\lambda y)^{\alpha-1}e^{-\lambda y}}{\Gamma(\alpha)}\;dy

    • إذا كانت معلمة الشكل α تساوي 1، فإن توزيع جاما يعادل التوزيع الأسي بنفس معلمة المقياس α.

    X\sim \Gamma(1,\lambda) \ \color{orange}\bm{\longrightarrow}\color{black} \ X\sim \text{Exp}(\lambda)

    • عندما تكون معلمة المقياس lect متوسطة، فإن توزيع جاما يكون حالة خاصة لتوزيع مربع كاي .

    \displaystyle X\sim \Gamma\left(\frac{n}{2},\frac{1}{2}\right) \text{con } n\in \mathbb{N}\ \color{orange}\bm{\longrightarrow}\color{black} \ X\sim \chi_n^2

    About Author

    دكتور بنيامين أندرسون
    دكتور بنيامين أندرسون

    مرحبًا، أنا بنجامين، أستاذ الإحصاء المتقاعد الذي تحول إلى مدرس متخصص في Statorials. بفضل خبرتي الواسعة في مجال الإحصاء، فأنا حريص على مشاركة معرفتي لتمكين الطلاب من خلال Statorials. تعرف أكثر

    Add a Comment

    ایمئیل یایینلانمایاجاق ایسته‎نیله‎ن بوشلوقلار خاللانمیشدیر *