كيفية حساب الارتباط بين المتغيرات الفئوية

غالبًا ما نستخدم معامل ارتباط بيرسون لحساب الارتباط بين المتغيرات العددية المستمرة.

ومع ذلك، نحتاج إلى استخدام مقياس مختلف لحساب الارتباط بين المتغيرات الفئوية، أي المتغيرات التي تأخذ أسماء أو تسميات مثل:

• الحالة الاجتماعية (أعزب، متزوج، مطلق)
• حالة التدخين (مدخن، غير مدخن)
• لون العين (أزرق، بني، أخضر)

هناك ثلاثة مقاييس شائعة الاستخدام لحساب الارتباط بين المتغيرات الفئوية:

1. الارتباط الرباعي: يستخدم لحساب الارتباط بين المتغيرات الفئوية الثنائية.

2. الارتباط متعدد الألوان: يستخدم لحساب الارتباط بين المتغيرات الفئوية الترتيبية.

3. معادلة كرامر V: تستخدم لحساب الارتباط بين المتغيرات الفئوية الاسمية.

توفر الأقسام التالية مثالاً لكيفية حساب كل من هذه القياسات الثلاثة.

متري 1: الارتباط رباعي

يتم استخدام الارتباط الرباعي لحساب الارتباط بين المتغيرات الفئوية الثنائية. تذكر أن المتغيرات الثنائية هي متغيرات يمكن أن تأخذ واحدة فقط من القيمتين المحتملتين.

تتراوح قيمة الارتباط التتراكوريكي من -1 إلى 1، حيث يشير -1 إلى وجود ارتباط سلبي قوي، ويشير 0 إلى عدم وجود ارتباط، ويشير 1 إلى ارتباط إيجابي قوي.

على سبيل المثال، لنفترض أننا نريد معرفة ما إذا كان الجنس مرتبطًا بتفضيل حزب سياسي أم لا. لذلك أخذنا عينة عشوائية بسيطة من 100 ناخب وسألناهم عن تفضيلهم لحزب سياسي.

ويعرض الجدول التالي نتائج الاستطلاع:

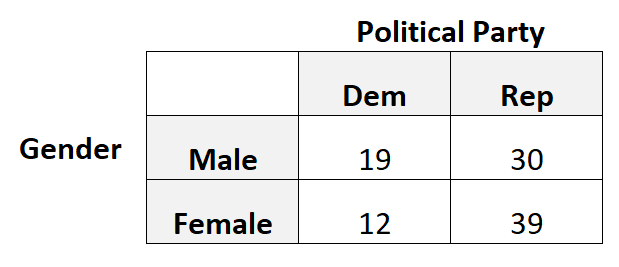
سوف نستخدم الارتباط الرباعي في هذا السيناريو لأن كل متغير فئوي هو ثنائي، أي أن كل متغير يمكن أن يأخذ قيمتين محتملتين فقط.

يمكننا استخدام الكود التالي في R لحساب الارتباط الرباعي بين المتغيرين:

 library (psych)

#create 2x2 table
data = matrix(c(19, 12, 30, 39), nrow= 2 )

#view table
data

#calculate tetrachoric correlation
tetrachoric(data)

tetrachoric correlation 
[1] 0.27

تبين أن الارتباط الرباعي هو 0.27 . وهذه القيمة منخفضة للغاية، مما يشير إلى وجود ارتباط ضعيف (إن وجد) بين النوع الاجتماعي وتفضيل الحزب السياسي.

متري 2: الارتباط متعدد الألوان

يتم استخدام الارتباط متعدد الألوان لحساب الارتباط بين المتغيرات الفئوية الترتيبية. تذكر أن المتغيرات الترتيبية هي متغيرات ذات قيم محتملة لها ترتيب طبيعي.

تتراوح قيمة الارتباط متعدد الألوان من -1 إلى 1، حيث يشير -1 إلى ارتباط سلبي قوي، ويشير 0 إلى عدم وجود ارتباط، ويشير 1 إلى ارتباط إيجابي قوي.

على سبيل المثال، لنفترض أنك تريد معرفة ما إذا كانت هناك وكالتان مختلفتان لتقييم الأفلام لديهما علاقة عالية بين تقييمات الأفلام الخاصة بهما.

نطلب من كل وكالة تقييم 20 فيلمًا مختلفًا على مقياس من 1 إلى 3، حيث يشير الرقم 1 إلى “سيء”، ويشير 2 إلى “ضعيف”، ويشير 3 إلى “جيد”.

ويبين الجدول التالي النتائج:

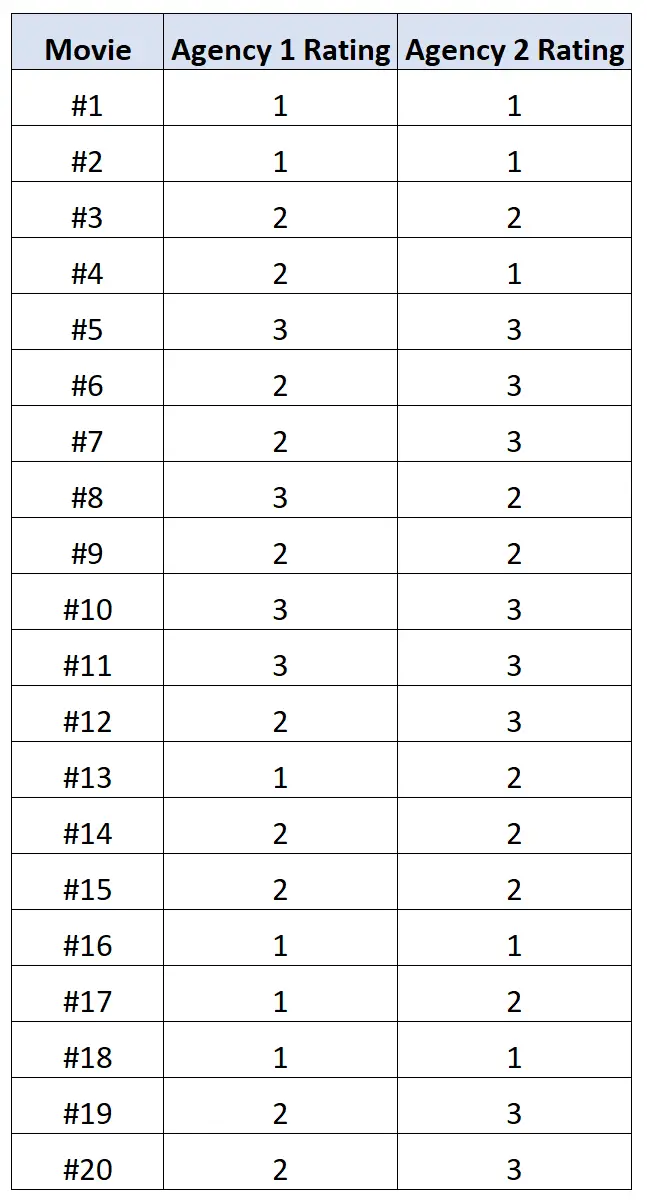
يمكننا استخدام الكود التالي في R لحساب الارتباط متعدد الألوان بين تصنيفات الوكالتين:

 library (polycor)

#define movie ratings
x <- c(1, 1, 2, 2, 3, 2, 2, 3, 2, 3, 3, 2, 1, 2, 2, 1, 1, 1, 2, 2)
y <- c(1, 1, 2, 1, 3, 3, 3, 2, 2, 3, 3, 3, 2, 2, 2, 1, 2, 1, 3, 3)

#calculate polychoric correlation between ratings
polychor(x, y)

[1] 0.7828328

وتبين أن الارتباط متعدد الألوان هو 0.78 . وهذه القيمة مرتفعة جدًا، مما يشير إلى وجود ارتباط إيجابي قوي بين تقييمات كل وكالة.

متري 3: كريمر V

يتم استخدام Cramer’s V لحساب الارتباط بين المتغيرات الفئوية الاسمية. تذكر أن المتغيرات الاسمية هي تلك التي تحمل تسميات الفئات ولكن ليس لها ترتيب طبيعي.

تتراوح قيمة Cramer’s V من 0 إلى 1، حيث يشير الرقم 0 إلى عدم وجود ارتباط بين المتغيرات ويشير الرقم 1 إلى وجود ارتباط قوي بين المتغيرات.

على سبيل المثال، لنفترض أننا نريد معرفة ما إذا كان هناك ارتباط بين لون العين والجنس. ولذلك قمنا بسؤال 50 شخصًا وحصلنا على النتائج التالية:

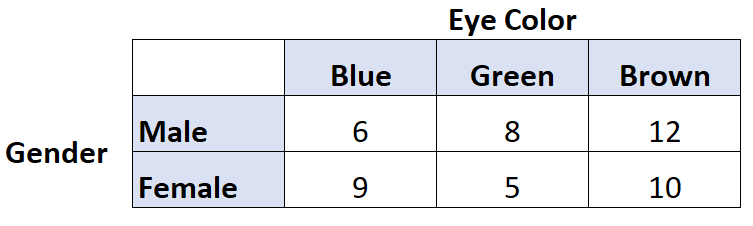
يمكننا استخدام الكود التالي في R لحساب Cramer’s V لهذين المتغيرين:

 library (rcompanion)

#create table
data = matrix(c(6, 9, 8, 5, 12, 10), nrow= 2 )

#view table
data

     [,1] [,2] [,3]
[1,] 6 8 12
[2,] 9 5 10

#calculate Cramer's V
cramerV(data)

Cramer V 
  0.1671

تبين أن قيمة Cramer’s V هي 0.1671 . وهذه القيمة منخفضة جدًا، مما يشير إلى وجود ارتباط ضعيف بين الجنس ولون العين.

مصادر إضافية

مقدمة لمعامل ارتباط بيرسون
مقدمة إلى الارتباط tetrachoric
المتغيرات الفئوية أو الكمية: ما الفرق؟
مستويات القياس: الاسمية والترتيبية والفاصلة والنسبة