هل السببية تعني الارتباط؟ (3 أمثلة)

ومن المعروف أن الارتباط لا يعني السببية .

وكمثال بسيط، إذا قمنا بجمع بيانات كل عام عن العدد الإجمالي لخريجي المدارس الثانوية وإجمالي استهلاك البيتزا في الولايات المتحدة، فسنجد أن المتغيرين مرتبطان بشكل كبير:

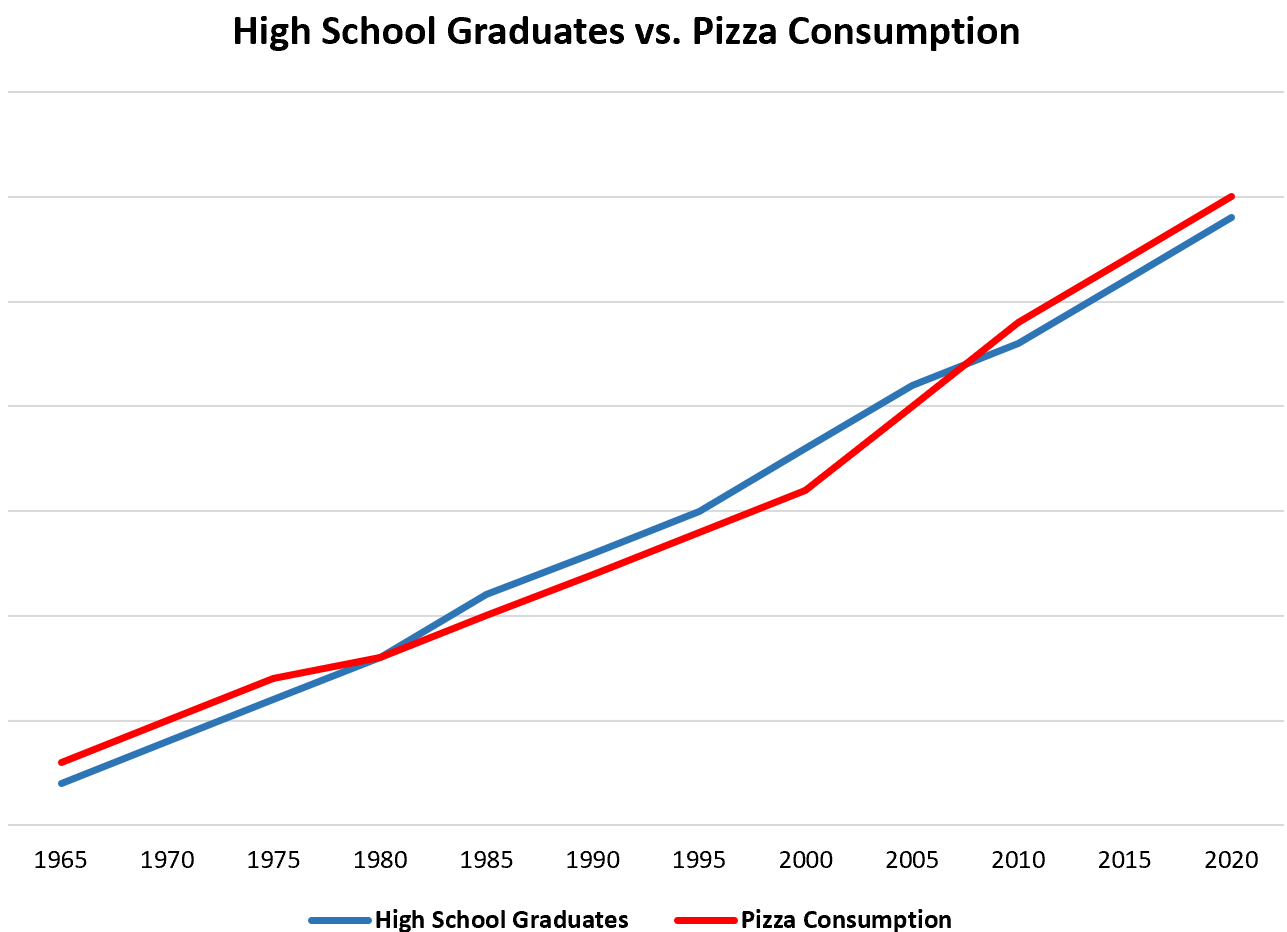
وهذا لا يعني أن زيادة عدد خريجي المدارس الثانوية يؤدي إلى زيادة استهلاك البيتزا.

التفسير الأكثر ترجيحاً هو أن عدد سكان الولايات المتحدة قد زاد بمرور الوقت، وهذا يعني أن عدد الأشخاص الحاصلين على شهادة الدراسة الثانوية والكمية الإجمالية للبيتزا المستهلكة تزداد مع زيادة عدد السكان.

ولكن ماذا عن العبارة المعاكسة: هل السببية تعني الارتباط؟

إذا تسبب متغير واحد في متغير آخر، فهل يعني ذلك بالضرورة أن المتغيرين سيكونان مرتبطين؟

الجواب القصير: لا.

توضح الأمثلة التالية السبب.

مثال 1: العلاقة التربيعية

لنفترض أن المتغير X يجعل المتغير Y يأخذ قيمة تساوي X ² .

على سبيل المثال:

• إذا كان X = -10 فإن Y = -10 ² = 100
• إذا كان X = 0 فإن Y = 0 ² = 0
• إذا كان X = 10 فإن Y = 10 ² = 100

وما إلى ذلك وهلم جرا.

إذا رسمنا العلاقة بين X و Y، فستبدو كما يلي:

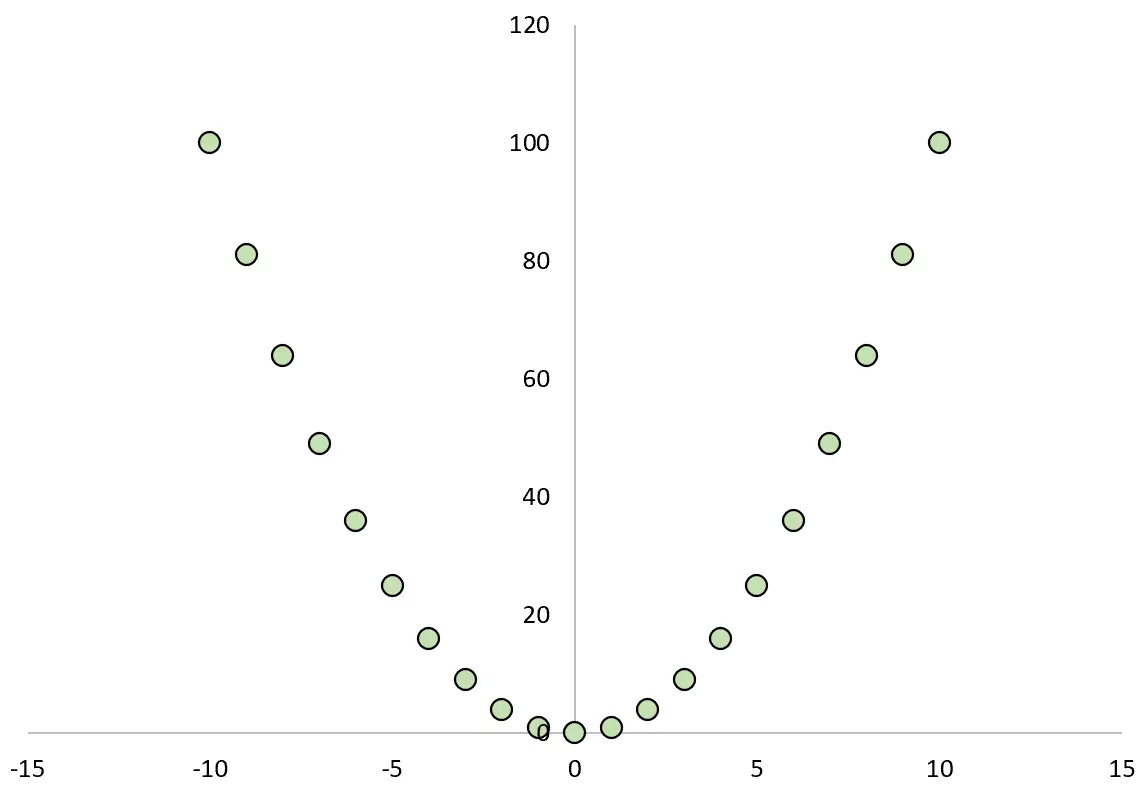
وإذا حسبنا معامل ارتباط بيرسون بين المتغيرين نجد أن الارتباط يساوي صفراً .

على الرغم من أن X يسبب Y، فإن الارتباط الخطي بين المتغيرين هو صفر.

مثال 2: العلاقة من الدرجة الرابعة

لنفترض أن المتغير X يجعل المتغير Y يأخذ قيمة تساوي X ⁴ .

على سبيل المثال:

• إذا كان X = -10 فإن Y = -10 ⁴ = 10,000
• إذا كان X = 0 فإن Y = 0 ⁴ = 0
• إذا كان X = 10 فإن Y = 10 ⁴ = 10,000

وما إلى ذلك وهلم جرا.

إذا رسمنا العلاقة بين X و Y، فستبدو كما يلي:

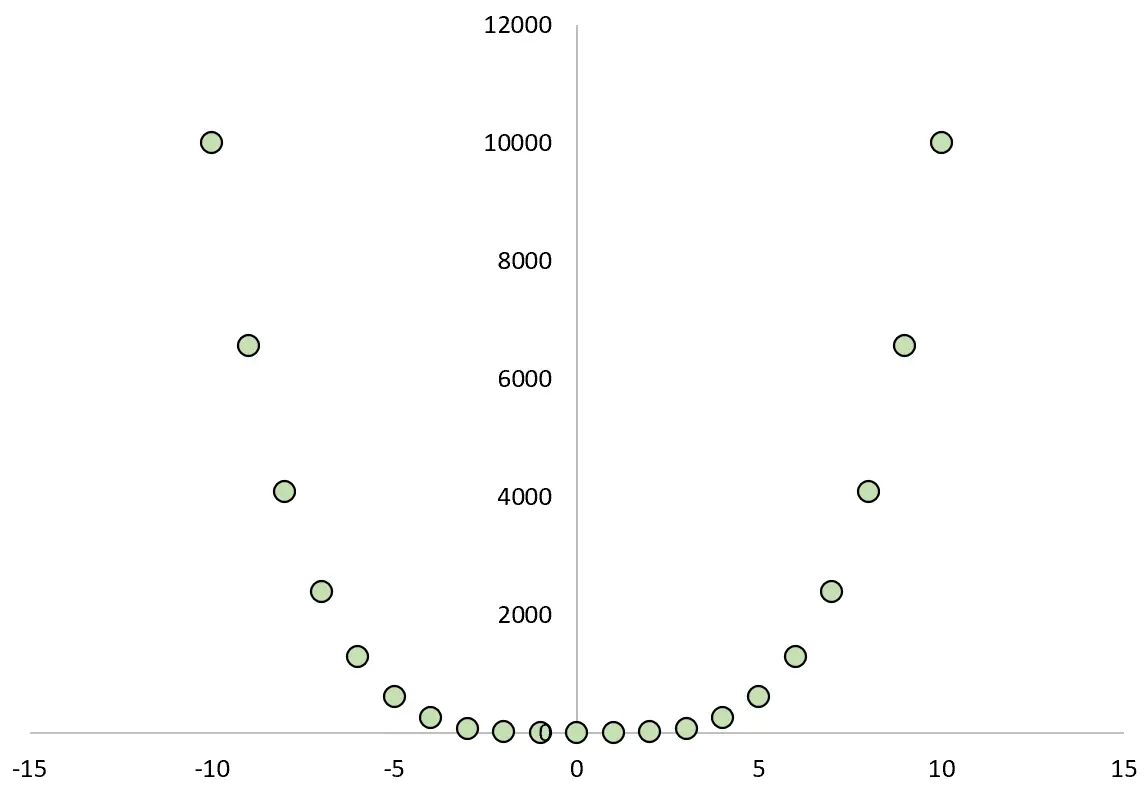
وإذا حسبنا معامل ارتباط بيرسون بين المتغيرين نجد أن الارتباط يساوي صفراً .

نحن نعلم أن X يسبب Y، ولكن الارتباط الخطي بين المتغيرين هو صفر.

مثال 3: علاقة جيب التمام

لنفترض أن المتغير X يجعل المتغير Y يأخذ قيمة تساوي cos(X).

على سبيل المثال:

• إذا كانت X = -10 فإن Y = cos(-10) = -0.83907
• إذا كانت X = 0 فإن Y = cos(0) = 1
• إذا كانت X = 10 فإن Y = cos(10) = -0.83907

وما إلى ذلك وهلم جرا.

إذا رسمنا العلاقة بين X و Y، فستبدو كما يلي:

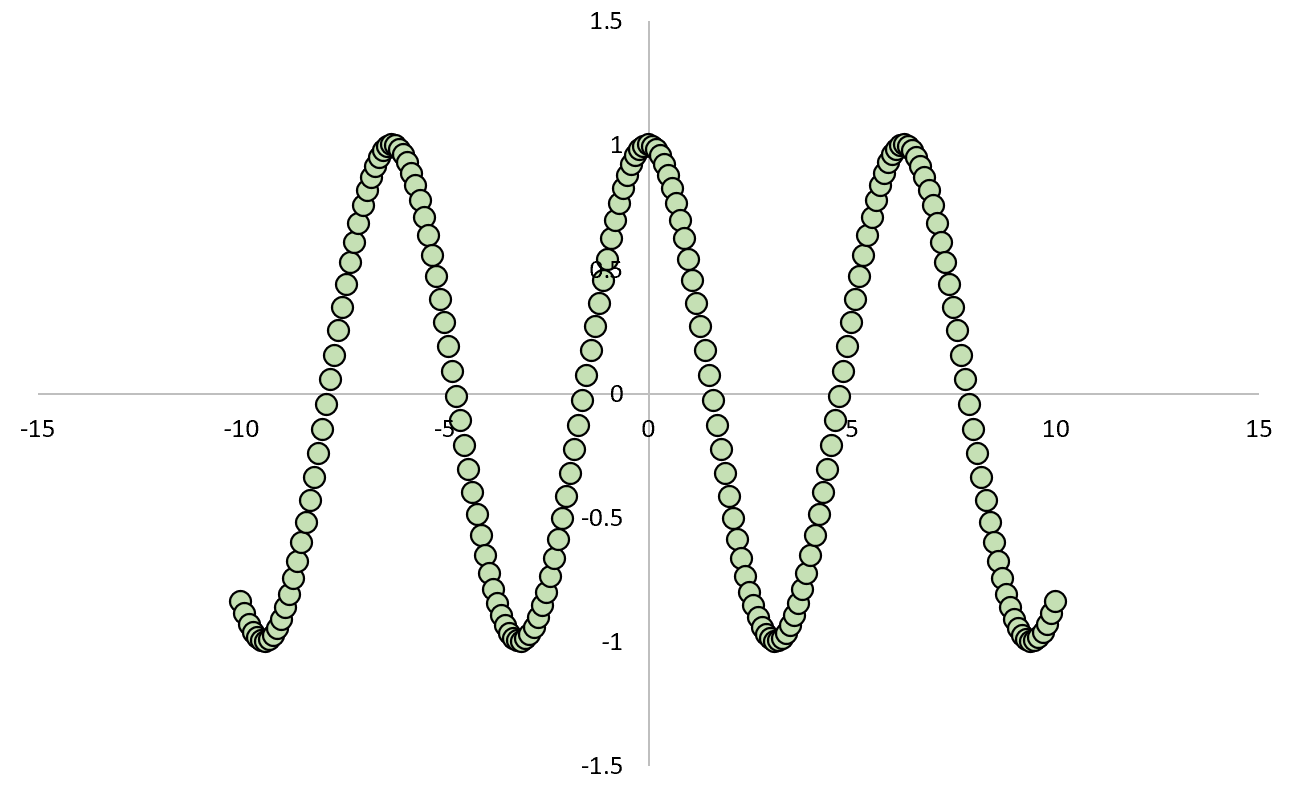
وإذا حسبنا معامل ارتباط بيرسون بين المتغيرين نجد أن الارتباط يساوي صفراً .

نحن نعلم أن X يسبب Y، ولكن الارتباط الخطي بين المتغيرين هو صفر.

مصادر إضافية

توفر البرامج التعليمية التالية معلومات إضافية حول الارتباط والسببية:

الارتباط لا يعني السببية: 5 أمثلة ملموسة
مقدمة لمعامل ارتباط بيرسون
السببية العكسية: التعريف والأمثلة