اختبار الفرضيات للاختلاف في الوسائل

By دكتور بنيامين أندرسون زومار 3, 2023 إحصائيات 0 Comments

تشرح هذه المقالة الفرق بين وسائل اختبار الفرضيات في الإحصائيات وما يتم استخدامه من أجله. وبالمثل، سوف تكتشف كيفية إجراء اختبار فرضيات حول الفرق في المتوسطات وتمرين تم حله خطوة بخطوة.

ما هو اختبار الفرضيات لفرق المتوسط؟

اختبار الفرضية للاختلاف في المتوسطات هو اختبار إحصائي يستخدم لرفض أو قبول الفرضية القائلة بأن متوسطي مجموعتين من السكان مختلفان. أي أن اختبار فرضية الفرق في الوسائل يستخدم لتحديد ما إذا كانت وسائل مجتمعين متماثلتين أم مختلفتين.

ضع في اعتبارك أن القرارات المتخذة في اختبار الفرضيات تعتمد على مستوى ثقة محدد مسبقًا، لذلك لا يمكن للمرء أن يضمن أن نتيجة اختبار الفرضية صحيحة دائمًا، بل أن النتيجة الأكثر ترجيحًا هي الصحيحة.

يتضمن اختبار الفرضية للفرق بين وسطين حساب إحصائية الاختبار ومقارنتها بالقيمة الحرجة لرفض الفرضية الصفرية أم لا. سنرى أدناه كيفية إجراء اختبار فرضي للفرق في الوسائل.

أخيرًا، تذكر أنه في الإحصائيات، قد يُطلق على اختبار الفرضيات أيضًا اسم تناقضات الفرضيات، أو اختبار الفرضيات، أو اختبار الأهمية.

➤ انظر: توزيع العينات للفرق في الوسائل

صيغة اختبار الفرضية للفرق في المتوسطات

تختلف الصيغة التي ينبغي استخدامها لاختبار الفرضيات حول الفرق في المتوسطات اعتمادًا على ما إذا كانت تباينات المجتمع معروفة، وإذا لم تكن معروفة، ما إذا كان من الممكن افتراض أنها متماثلة أو مختلفة. لذا، في هذا القسم، سنرى الصيغة التي يجب استخدامها اعتمادًا على الحالة.

الاختلافات المعروفة

إن صيغة حساب إحصائية اختبار الفرضية للفرق في المتوسطات عند معرفة التباينات هي كما يلي:

$\displaystyle Z=\frac{\displaystyle (\overline{x_1}-\overline{x_2})-(\mu_1-\mu_2)}{\displaystyle\sqrt{\frac{\sigma_1^2}{n_1}+\frac{\sigma_2^2}{n_2}}}$

ذهب:

$Z$

هي إحصائية اختبار الفرضية للفرق بين وسطين لهما تباين معروف، والذي يتبع التوزيع الطبيعي القياسي.
$\mu_1$

هو متوسط السكان 1.
$\mu_2$

هو متوسط عدد السكان 2.
$\overline{x_1}$

هو متوسط العينة 1.
$\overline{x_2}$

هو متوسط العينة 2.
$\sigma_1$

هو الانحراف المعياري للسكان 1.
$\sigma_2$

هو الانحراف المعياري للسكان 2.
$n_1$

حجم العينة 1.
$n_2$

حجم العينة 2.

ضع في اعتبارك أن هذه هي الحالة الأقل شيوعًا، لذلك يتم استخدام هذه الصيغة فقط في بعض الحالات المحددة.

انحرافات غير معروفة ومتساوية

إن صيغة حساب إحصائية اختبار الفرضية للفرق في الوسائل عندما تكون تباينات السكان غير معروفة ولكن من المفترض أنها متساوية هي:

$\displaystyle t=\frac{\displaystyle (\overline{x_1}-\overline{x_2})-(\mu_1-\mu_2)}{\displaystyle s_p\sqrt{\frac{1}{n_1}+\frac{1}{n_2}}}$

ذهب:

$t$

هي إحصائية اختبار الفرضية للفرق في الوسائل ذات التباينات غير المعروفة، والتي تتبع توزيع الطالب مع n ₁ + n ₂ -2 درجات الحرية.
$\mu_1$

هو متوسط السكان 1.
$\mu_2$

هو متوسط عدد السكان 2.
$\overline{x_1}$

هو متوسط العينة 1.
$\overline{x_2}$

هو متوسط العينة 2.
$s_p$

هو الانحراف المعياري المشترك.
$n_1$

حجم العينة 1.
$n_2$

حجم العينة 2.

يتم حساب الانحراف المعياري المشترك للعينتين بالصيغة التالية:

$\displaystyle s_p=\sqrt{\frac{(n_1-1)s_1^2+(n_2-1)s_2^2}{n_1+n_2-2}}$

اختلافات غير معروفة ومختلفة

عندما تكون تباينات المجتمع غير معروفة، وعلاوة على ذلك، يُفترض أنها مختلفة، تكون صيغة حساب إحصائية اختبار الفرضية للفرق في المتوسطات كما يلي:

$\displaystyle t=\frac{\displaystyle (\overline{x_1}-\overline{x_2})-(\mu_1-\mu_2)}{\displaystyle \sqrt{\frac{s_1^2}{n_1}+\frac{s_2^2}{n_2}}}$

ذهب:

$t$

هي إحصائية اختبار الفرضية للفرق في الوسائل ذات التباينات غير المعروفة، والتي تتبع توزيع الطالب.
$\mu_1$

هو متوسط السكان 1.
$\mu_2$

هو متوسط عدد السكان 2.
$\overline{x_1}$

هو متوسط العينة 1.
$\overline{x_2}$

هو متوسط العينة 2.
$\sigma_1$

هو الانحراف المعياري للسكان 1.
$\sigma_2$

هو الانحراف المعياري للسكان 2.
$n_1$

حجم العينة 1.
$n_2$

حجم العينة 2.

ومع ذلك، في هذه الحالة، يتم حساب درجات حرية توزيع الطالب باستخدام الصيغة التالية:

$\displaystyle GL=\frac{\displaystyle\left(\frac{s_1^2}{n_1}+\frac{s_2^2}{n_2}\right)^2}{\displaystyle\frac{\displaystyle\frac{s_1^2}{n_1}}{n_1-1}+\frac{\displaystyle\frac{s_2^2}{n_2}}{n_2-1}}$

➤ انظر: صيغة فترة الثقة لاختلاف الوسائل

مثال ملموس لاختبار الفرضيات للفرق في الوسائل

وللانتهاء من استيعاب مفهوم اختبار الفرضيات على اختلاف الوسائل سنرى مثالا ملموسا لهذا النوع من اختبارات الفرضيات.

تريد إجراء دراسة إحصائية عن راتب شركتين متنافستين، وبشكل أكثر تحديدًا، تريد تحديد ما إذا كان متوسط الراتب بين الشركتين مختلفًا. وللقيام بذلك تم أخذ عينة مكونة من 47 عاملاً من إحدى الشركات وعينة أخرى مكونة من 55 عاملاً من الشركة الأخرى. ويتم الحصول على متوسط راتب 40 ألف دولار وانحراف معياري 12 ألف دولار من العينة الأولى، في حين يتم الحصول على متوسط راتب 46 ألف دولار وانحراف معياري 18 ألف دولار من العينة الثانية. قم بإجراء اختبار فرضي بمستوى دلالة 5% لتحديد ما إذا كان متوسط الرواتب مختلفًا أم لا.

وفي هذه الحالة تكون الفرضية الصفرية والفرضية البديلة لاختبار الفرضية للفرق بين الوسطين كما يلي:

$\begin{cases}H_0: \mu_1-\mu_2=0\\[2ex] H_1:\mu_1-\mu_2\neq 0 \end{cases}$

في هذه الحالة، الفجوات السكانية غير معروفة، ولكن يمكن افتراض أنها متساوية لأنها شركات متنافسة وظروف العمل في السوق التي تعمل فيها متشابهة إلى حد كبير. ولذلك فإن صيغة إحصائية اختبار الفرضيات للفرق في الوسائل التي يجب أن نستخدمها هي:

$\displaystyle t=\frac{\displaystyle (\overline{x_1}-\overline{x_2})-(\mu_1-\mu_2)}{\displaystyle s_p\sqrt{\frac{1}{n_1}+\frac{1}{n_2}}}$

لذلك نحسب الانحراف المعياري المجمع للعينتين:

$\begin{aligned}\displaystyle s_p&=\sqrt{\frac{(n_1-1)s_1^2+(n_2-1)s_2^2}{n_1+n_2-2}}\\[2ex]\displaystyle s_p&=\sqrt{\frac{(47-1)\cdot 12000^2+(55-1)\cdot 18000^2}{47+55-2}}\\[2ex]s_p&=15530,61\end{aligned}$

نطبق الآن صيغة اختبار الفرضيات للفرق في الوسائل:

$\displaystyle t=\frac{\displaystyle (\overline{x_1}-\overline{x_2})-(\mu_1-\mu_2)}{\displaystyle s_p\sqrt{\frac{1}{n_1}+\frac{1}{n_2}}}=\cfrac{(40000-46000)-0}{\displaystyle 15530,61\sqrt{\frac{1}{47}+\frac{1}{55}}}=-1,94$

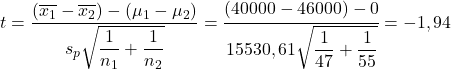
ومن ناحية أخرى نبحث عن القيمة الحرجة لاختبار الفرضيات للفرق بين المتوسطات في جدول t للطالب :

$\alpha=0,05 \ \color{orange}\bm{\longrightarrow}\color{black}\ \alpha/2=0,025$

$\begin{array}{c}t_{\alpha/2| n_1+n_2-2}= \ \color{orange}\bm{?}\\[4ex]t_{0,025| 100}=1,984\end{array}$

وبما أن القيمة المطلقة لإحصائية الاختبار أقل من قيمة الاختبار الحرجة، يتم قبول الفرضية الصفرية ورفض الفرضية البديلة.

$|-1,94|=1,94<1,984 \ \color{orange}\bm{\longrightarrow}\color{black} \ \text{Se rechaza } H_1$

About Author

دكتور بنيامين أندرسون

مرحبًا، أنا بنجامين، أستاذ الإحصاء المتقاعد الذي تحول إلى مدرس متخصص في Statorials. بفضل خبرتي الواسعة في مجال الإحصاء، فأنا حريص على مشاركة معرفتي لتمكين الطلاب من خلال Statorials. تعرف أكثر

ما هو اختبار الفرضيات لفرق المتوسط؟

صيغة اختبار الفرضية للفرق في المتوسطات

الاختلافات المعروفة

انحرافات غير معروفة ومتساوية

اختلافات غير معروفة ومختلفة

مثال ملموس لاختبار الفرضيات للفرق في الوسائل

About Author

دكتور بنيامين أندرسون

Add a Comment