كيفية العثور على مدى مؤامرة مربع: مع أمثلة

المخطط الصندوقي هو نوع من المخطط يعرض ملخصًا مكونًا من خمسة أرقام لمجموعة بيانات، والذي يتضمن:

• الحد الأدنى للقيمة
• الربع الأول (المئوية الخامسة والعشرون)
• القيمة المتوسطة
• الربع الثالث (المئوي 75)
• القيمة القصوى

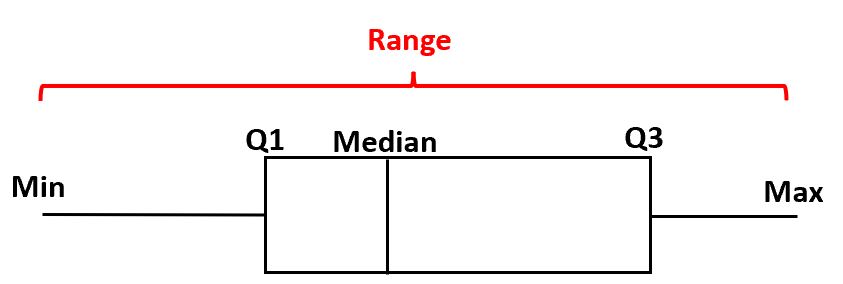
لعمل مخطط مربع، نرسم مربعًا من الربع الأول إلى الربع الثالث. بعد ذلك، نرسم خطًا رأسيًا في المنتصف. وأخيرًا، نرسم “شوارب” الربعيات حتى القيمة الدنيا والقصوى.

نطاق boxplot هو الفرق بين القيمة القصوى والحد الأدنى للقيمة.

• النطاق = الحد الأقصى – الحد الأدنى

للعثور على مدى مخطط مربع معين، يمكننا ببساطة طرح القيمة الموجودة في الخط الطولي السفلي من القيمة الموجودة في الخط الطولي العلوي.

توضح الأمثلة التالية كيفية العثور على مدى مخطط الصندوق عمليًا.

مثال 1: نتائج الامتحان

يوضح الشكل المربع التالي توزيع الدرجات في امتحان جامعي معين. ما هو نطاق نتائج الامتحان؟

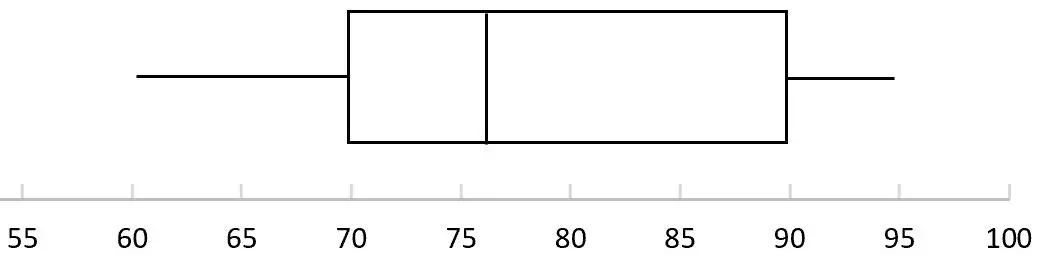
يمكننا العثور على القيم التالية على boxplot للإجابة على هذا السؤال:

• النطاق = الحد الأقصى – الحد الأدنى
• النطاق = 95 – 60
• المدى = 35

نطاق نتائج الامتحان هو 35 .

مثال 2: النقاط المسجلة

يوضح الشكل المربع التالي توزيع النقاط التي سجلها لاعبو كرة السلة في دوري معين. ما مدى انتشار التوزيع؟

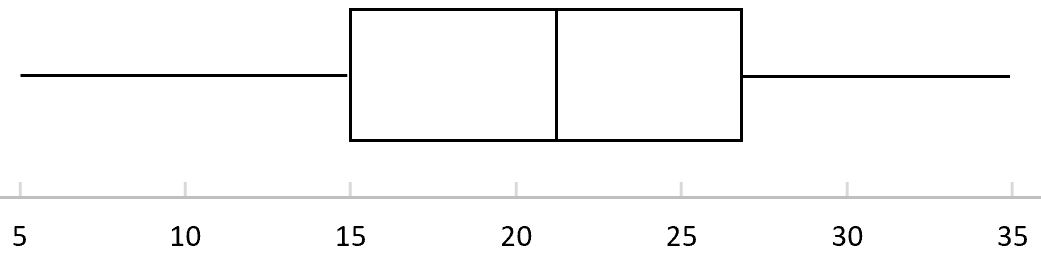
يمكننا العثور على القيم التالية على boxplot للإجابة على هذا السؤال:

• النطاق = الحد الأقصى – الحد الأدنى
• النطاق = 35 – 5
• المدى = 30

حجم التوزيع 30 .

مثال 3: مقارنة ارتفاعات النباتات

توضح المخططات المربعة التالية توزيع الارتفاع لنوعين نباتيين مختلفين: الأحمر والأزرق. أي توزيع له وصول أكبر؟

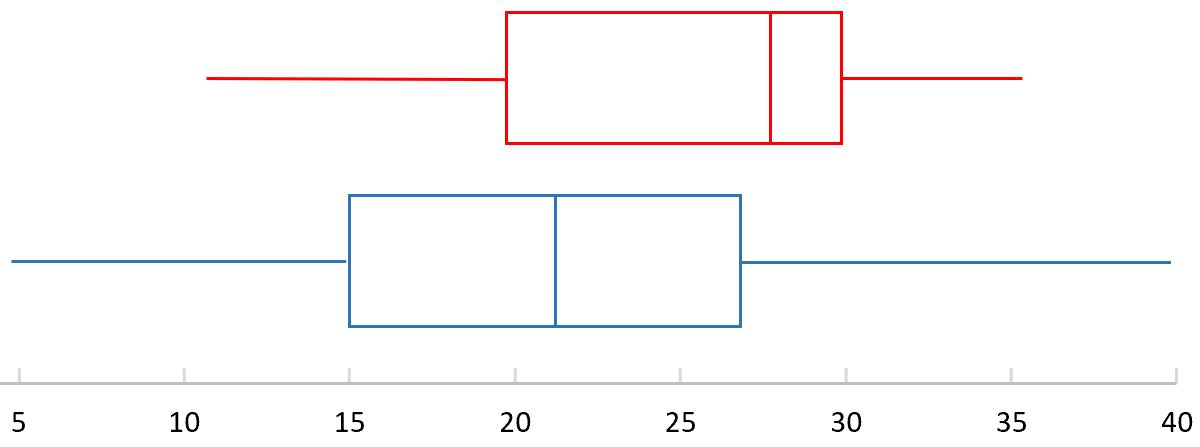
أولا، دعونا نجد مدى المربع الأحمر:

• النطاق = الحد الأقصى – الحد الأدنى
• النطاق = 35 – 10
• المدى = 25

بعد ذلك، دعونا نجد مدى مؤامرة الصندوق الأزرق:

• النطاق = الحد الأقصى – الحد الأدنى
• النطاق = 40 – 5
• المدى = 35

مساحة توزيع الأنواع الزرقاء أكبر.

مصادر إضافية

توفر البرامج التعليمية التالية معلومات إضافية حول مخططات الصندوق:

مولد مؤامرة مربع
كيفية مقارنة مؤامرات الصندوق
كيفية تحديد عدم التماثل في مخططات الصندوق
كيفية العثور على المدى الربيعي لboxplot