الانحدار اللوجستي
تشرح هذه المقالة ماهية الانحدار اللوجستي في الإحصائيات. وبالمثل، ستجد صيغة الانحدار اللوجستي، وما هي الأنواع المختلفة للانحدار اللوجستي، بالإضافة إلى تمرين الانحدار اللوجستي الذي تم حله.
ما هو الانحدار اللوجستي؟
في الإحصاء، الانحدار اللوجستي هو نوع من نماذج الانحدار المستخدمة للتنبؤ بنتيجة متغير فئوي . أي أنه يتم استخدام الانحدار اللوجستي لنمذجة احتمالية أن يأخذ المتغير الفئوي قيمة معينة بناءً على المتغيرات المستقلة.
نموذج الانحدار اللوجستي الأكثر شيوعًا هو الانحدار اللوجستي الثنائي، حيث لا يوجد سوى نتيجتين محتملتين: “الفشل” أو “النجاح” ( توزيع برنولي ). ويمثل “الفشل” بالقيمة 0، بينما يمثل “النجاح” بالقيمة 1.
على سبيل المثال، يمكن دراسة احتمال اجتياز الطالب لامتحان بناءً على الساعات التي قضاها في الدراسة باستخدام نموذج الانحدار اللوجستي. وفي هذه الحالة يكون الفشل نتيجة “الفشل”، ومن ناحية أخرى، يكون النجاح نتيجة “النجاح”.
صيغة الانحدار اللوجستي
معادلة نموذج الانحدار اللوجستي هي:
![]()
لذلك، في نموذج الانحدار اللوجستي، يتم حساب احتمال الحصول على نتيجة “النجاح”، أي أن المتغير التابع يأخذ القيمة 1، يتم حسابه بالمعادلة التالية:
![]()
ذهب:
-

هو احتمال أن يكون المتغير التابع هو 1.
-

هو ثابت نموذج الانحدار اللوجستي.
-

هو معامل الانحدار للمتغير i.
-

هي قيمة المتغير i .
مثال على نموذج الانحدار اللوجستي
الآن بعد أن عرفنا تعريف الانحدار اللوجستي، دعونا نرى مثالاً ملموسًا لكيفية إنشاء نموذج لهذا النوع من الانحدار.
- في الجدول التالي، تم تجميع سلسلة من 20 قطعة من البيانات التي تتعلق بساعات دراسة كل طالب وما إذا كان قد نجح أو فشل في اختبار الإحصاء. قم بتشغيل نموذج الانحدار اللوجستي واحسب احتمال نجاح الطالب إذا درس لمدة 4 ساعات.
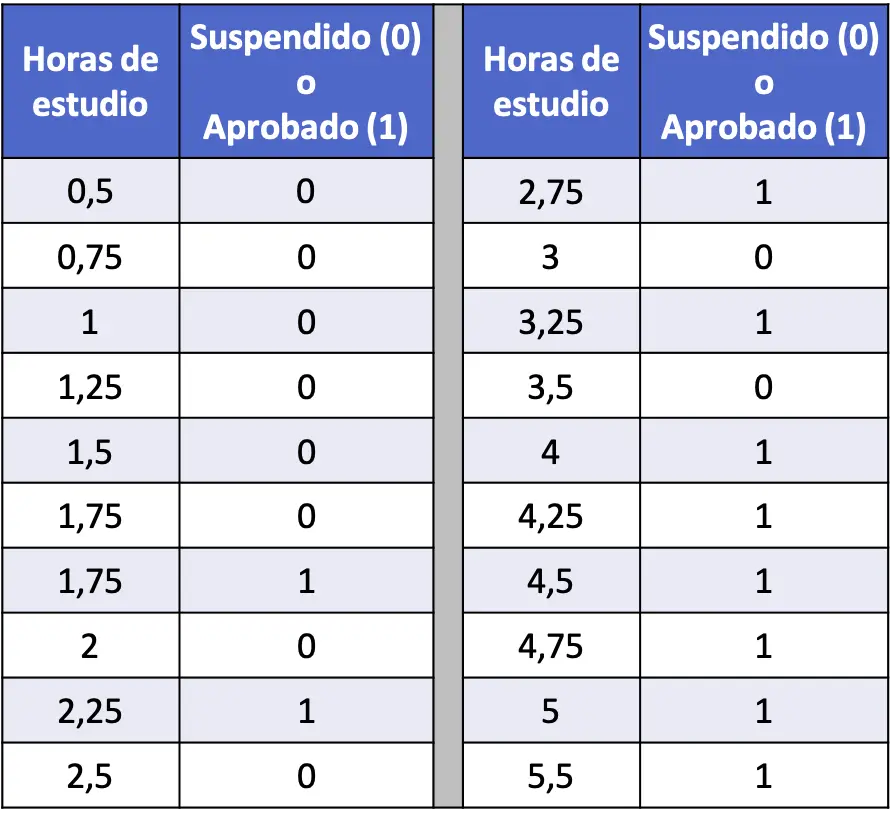
وفي هذه الحالة يكون المتغير التوضيحي هو عدد ساعات الدراسة ومتغير الاستجابة هو ما إذا كان الطالب راسباً (0) أو ناجحاً (1). ولذلك، في نموذجنا سيكون لدينا المعامل فقط
![]()
والمعامل
![]()
نظرًا لوجود متغير مستقل واحد فقط.
![]()
يعد التحديد اليدوي لمعاملات الانحدار أمرًا شاقًا للغاية، لذا يوصى باستخدام برامج الكمبيوتر مثل Minitab. وبذلك تكون قيم معاملات الانحدار المحسوبة باستخدام برنامج Minitab كما يلي:
![Rendered by QuickLaTeX.com \begin{array}{c}\beta_0\approx -4,1\\[2ex]\beta_1\approx 1,5\end{array}](https://statorials.org/wp-content/ql-cache/quicklatex.com-6ed66de602220c69aabb71a726fec9f8_l3.png)
وبالتالي فإن نموذج الانحدار اللوجستي هو كما يلي:
![Rendered by QuickLaTeX.com \begin{aligned}p&=\cfrac{1}{1+e^{-(\beta_0+\beta_1x_1+\beta_2x_2+\dots+\beta_ix_i)}}\\[2ex]p&=\cfrac{1}{1+e^{-(-4,1+1,5x_1)}}\\[2ex]p&=\cfrac{1}{1+e^{4,1-1,5x_1}}\end{aligned}](https://statorials.org/wp-content/ql-cache/quicklatex.com-0902ac67194bedf38d5f4ff06dc27a38_l3.png)
يمكنك أدناه رؤية نموذج البيانات ومعادلة نموذج الانحدار اللوجستي المرسومة بيانيًا:
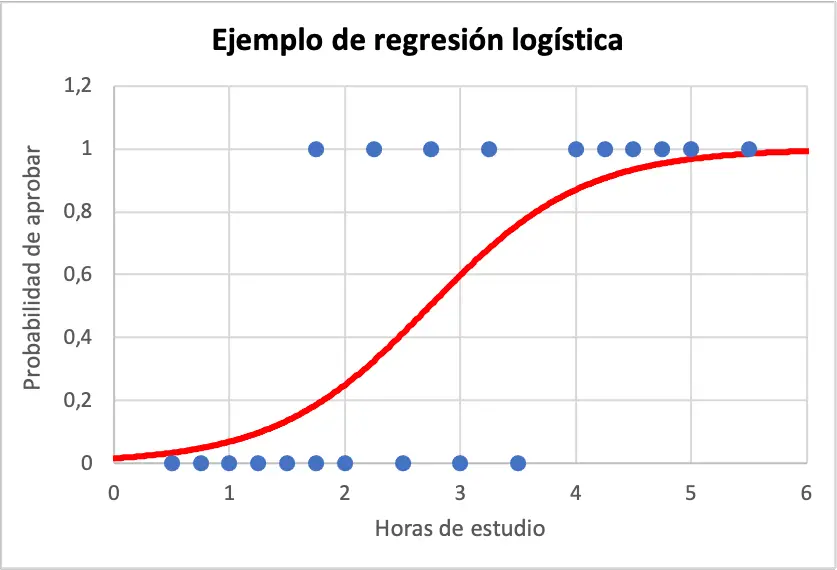
وبالتالي، لحساب احتمال نجاح الطالب إذا درس 4 ساعات، ما عليك سوى استخدام المعادلة التي تم الحصول عليها من نموذج الانحدار اللوجستي:
![Rendered by QuickLaTeX.com \begin{aligned}p&=\cfrac{1}{1+e^{4,1-1,5x_1}}\\[2ex]p&=\cfrac{1}{1+e^{4,1-1,5\cdot 4}}\\[2ex]p&=0,8699\end{aligned}](https://statorials.org/wp-content/ql-cache/quicklatex.com-930691eafee62c04e59d9c4de8ef6a76_l3.png)
باختصار، إذا درس الطالب لمدة أربع ساعات، سيكون لديه احتمال اجتياز الامتحان بنسبة 86.99%.
أنواع الانحدار اللوجستي
هناك ثلاثة أنواع من الانحدار اللوجستي :
- الانحدار اللوجستي الثنائي : يمكن أن يحتوي المتغير التابع على قيمتين فقط (0 و 1).
- الانحدار اللوجستي متعدد الحدود : يحتوي المتغير التابع على أكثر من قيمتين محتملتين.
- الانحدار اللوجستي الترتيبي : النتائج المحتملة لها ترتيب طبيعي.
الانحدار اللوجستي والانحدار الخطي
وأخيرا، باختصار، سنرى ما هو الفرق بين الانحدار اللوجستي والانحدار الخطي، حيث أن نموذج الانحدار الأكثر استخداما في الإحصاء هو النموذج الخطي.
يستخدم الانحدار الخطي لنمذجة المتغيرات الرقمية التابعة. بالإضافة إلى ذلك، في الانحدار الخطي، تكون العلاقة بين المتغيرات التوضيحية ومتغير الاستجابة خطية.
ولذلك، فإن الفرق الرئيسي بين الانحدار اللوجستي والانحدار الخطي هو نوع المتغير التابع. في الانحدار اللوجستي، يكون المتغير التابع قاطعًا، في حين أن المتغير التابع في الانحدار الخطي يكون رقميًا.
وبالتالي، يتم استخدام الانحدار اللوجستي للتنبؤ بنتيجة بين خيارين محتملين، في حين يساعد الانحدار الخطي على التنبؤ بنتيجة عددية.