التغايرية
تشرح هذه المقالة ماهية التغايرية في الإحصائيات. بالإضافة إلى ذلك، سوف تكتشف أسباب عدم التجانس، وما هي عواقبه، وكيفية إصلاحه.
ما هي التغايرية؟
في الإحصاء، تعد التغايرية خاصية تقدم نمط انحدار يشير ضمنًا إلى أن تباين الخطأ ليس ثابتًا. بمعنى آخر، النموذج المتغاير يعني أن أخطاءه ذات تباين غير منتظم، ومن ثم يسمى النموذج متغايراً.
تذكر أن الخطأ (أو المتبقي) يتم تعريفه على أنه الفرق بين القيمة الحقيقية والقيمة المقدرة بواسطة نموذج الانحدار.
![]()
عند بناء نموذج الانحدار، يتم حساب الخطأ الناتج عن كل ملاحظة باستخدام التعبير السابق. وبالتالي، يكون النموذج الإحصائي متغايرًا عندما لا يكون تباين الأخطاء المحسوبة ثابتًا خلال الملاحظات، بل يختلف.
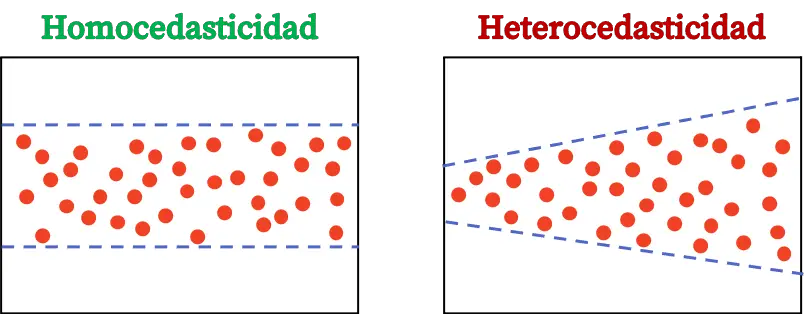
على الرغم من أن الأمر قد يبدو بسيطًا للغاية، إلا أنه من المهم ألا يقدم نموذج الانحدار تباينًا متباينًا، نظرًا لأن حساب النموذج يعتمد على حقيقة أن تباين البقايا ثابت، وهو في الواقع أحد الافتراضات السابقة لـ نماذج الانحدار.
هناك بعض الاختبارات الإحصائية التي يمكنها الكشف عن التغايرية، مثل اختبار وايت أو اختبار جولدفيلد كواندت. ومع ذلك، عادة من خلال رسم بياني للبقايا، يمكن تحديد تغايرها.
أسباب التغايرية
الأسباب الأكثر شيوعًا للتغايرية في النموذج هي:
- عندما يكون نطاق البيانات واسعًا جدًا مقارنة بالمتوسط. إذا كانت هناك قيم كبيرة جدًا وقيم صغيرة جدًا في نفس العينة الإحصائية، فمن المحتمل أن يكون نموذج الانحدار الذي تم الحصول عليه متغايرًا.
- يؤدي حذف المتغيرات في نموذج الانحدار أيضًا إلى عدم تجانس البيانات. ومن الناحية المنطقية، إذا لم يتم تضمين متغير ذي صلة في النموذج، فسيتم تضمين تغيره في البقايا ولن يتم إصلاح ذلك بالضرورة.
- وبالمثل، قد يؤدي التغيير في البنية إلى عدم ملاءمة النموذج لمجموعة البيانات، وبالتالي، قد لا يكون تباين البقايا ثابتًا.
- عندما تكون لبعض المتغيرات قيم أكبر بكثير من المتغيرات التوضيحية الأخرى، فقد يكون للنموذج تغايرية. في هذه الحالة، يمكن نسبية المتغيرات لحل المشكلة.
ومع ذلك، فإن بعض الحالات، بطبيعتها، من المحتمل أن تظهر تغايرًا. على سبيل المثال، إذا قمنا بنمذجة دخل شخص ما من خلال إنفاقه على الطعام، فإن الأشخاص الأكثر ثراءً لديهم تباين أكبر بكثير في إنفاقهم على الطعام مقارنة بالأشخاص الأكثر فقراً. لأن الغني يأكل أحياناً في مطاعم غالية وأحياناً أخرى في مطاعم رخيصة، على عكس الفقير الذي يأكل دائماً في المطاعم الرخيصة. لذلك، من السهل أن يمتلك نموذج الانحدار تباينًا متباينًا.
عواقب التغاير
بشكل رئيسي، فإن عواقب التغايرية في نموذج الانحدار هي كما يلي:
- يتم فقدان الكفاءة في مقدر المربعات الصغرى، والذي يعرف بأنه متوسط مربعات الأخطاء.
- تحدث أخطاء في حساب مصفوفة التغاير لمقدرات المربعات الصغرى.
التغاير الصحيح
عندما يكون نموذج الانحدار الناتج متغايرًا، يمكننا تجربة التصحيحات التالية للحصول على متغايرية:
- احسب اللوغاريتم الطبيعي للمتغير المستقل، وهذا مفيد بشكل عام عندما يزيد تباين البقايا في الرسم البياني.
- اعتمادًا على قطعة الأرض المتبقية، قد يكون هناك نوع آخر من تحويل المتغير المستقل أكثر عملية. على سبيل المثال، إذا كان الرسم البياني على شكل قطع مكافئ، فيمكننا حساب مربع المتغير المستقل وإضافة هذا المتغير إلى النموذج.
- يمكن أيضًا استخدام متغيرات أخرى للنموذج؛ عن طريق إزالة أو إضافة متغير، يمكن تعديل تباين البقايا.
- بدلاً من استخدام معيار المربعات الصغرى، يمكن استخدام معيار المربعات الصغرى المرجحة.
التغاير والمثلية
أخيرًا، سنرى ما هي الاختلافات بين التغاير والتجانس في الإحصاء، حيث أن هذين مفهومين لنماذج الانحدار التي يجب أن نكون واضحين بشأنها.
إن تجانس نموذج الانحدار هو خاصية إحصائية تشير إلى أن تباين الخطأ ثابت. وبالتالي، فإن النموذج المثلي يعني أن تباين أخطائه ثابت.
تم العثور على الفرق بين التغاير والتجانس في ثبات تباين البقايا. إذا كان تباين بقايا النموذج غير ثابت، فهذا يعني أن النموذج متغاير. ومن ناحية أخرى، إذا كان تباين البقايا ثابتا، فهذا يعني أنه متجانس.
لذلك، نحتاج إلى التأكد من أن نموذج الانحدار الذي نبنيه هو نموذج متجانس، وبهذه الطريقة سيتم تلبية الافتراض القائل بأن تباين القيم المتبقية ثابت.