كيفية تفسير الانحراف المعياري للصفر
في الإحصاء، يستخدم الانحراف المعياري لقياس توزيع القيم في العينة.
يمكننا استخدام الصيغة التالية لحساب الانحراف المعياري لعينة معينة:
√ Σ(س ط – س بار ) 2 / (ن-1)
ذهب:
- Σ: رمز يعني “المجموع”
- xi : القيمة i للعينة
- شريط x: يعني العينة
- ن: حجم العينة
كلما زادت قيمة الانحراف المعياري، زادت تشتت القيم في العينة .
كلما انخفضت قيمة الانحراف المعياري، كلما تم تجميع القيم معًا بشكل أوثق.
إذا كان الانحراف المعياري للعينة صفراً، فهذا يعني أن جميع القيم في العينة متماثلة تماماً.
وبعبارة أخرى، لا توجد فجوة بين القيم.
يوضح المثال التالي كيفية تفسير الانحراف المعياري للصفر في الممارسة العملية.
مثال: كيفية تفسير الانحراف المعياري للصفر
لنفترض أننا جمعنا عينة عشوائية بسيطة مكونة من 10 سحالي وقمنا بقياس أطوالها (بالبوصة):
الأطوال : 7, 7, 7, 7, 7, 7, 7, 7, 7, 7
ويبلغ متوسط طول السحالي في العينة 7 بوصات.
بمعرفة ذلك، يمكننا حساب عينة الانحراف المعياري لمجموعة البيانات هذه:
- ق = √ Σ(س ط – س بار ) 2 / (ن-1)
- ق = √ ((7 – 7) 2 + (7 – 7) 2 + (7 – 7) 2 + … + (7 – 7) 2 / (10-1)
- ق = √ 0 2 + 0 2 + 0 2 + … + 0 2 / 9
- ق = 0
تبين أن الانحراف المعياري للعينة هو 0 .
نظرًا لأن كل سحلية لها نفس الطول تمامًا، فإن توزيع القيم في مجموعة البيانات يكون صفرًا تمامًا.
هل سيكون الانحراف المعياري صفرًا في العالم الحقيقي؟
من الممكن تمامًا أن يكون لمجموعة بيانات العالم الحقيقي انحراف معياري قدره صفر، لكن هذا نادر.
السيناريو الأكثر احتمالاً الذي قد تواجه فيه انحرافًا معياريًا قدره صفر هو عند جمع عينات صغيرة للأحداث النادرة.
على سبيل المثال، لنفترض أنك تقوم بجمع بيانات حول عدد حوادث الطرق خلال فترة أسبوع واحد في مدينة معينة.
من الممكن تمامًا أن تقوم بجمع البيانات التالية:
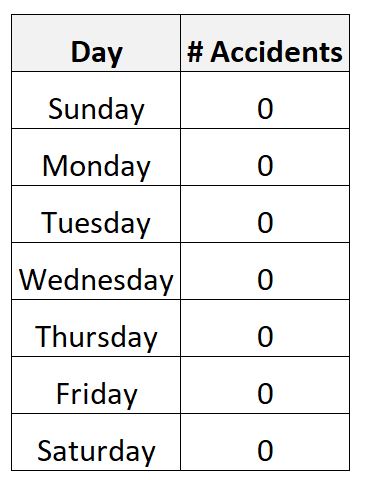
في هذا السيناريو، سيكون متوسط عدد الحوادث اليومية صفرًا وسيكون الانحراف المعياري صفرًا أيضًا.
أو ربما تقوم بجمع البيانات التالية حول عدد المبيعات الشهرية لمنتج باهظ الثمن لشركة ما خلال فترة 6 أشهر:
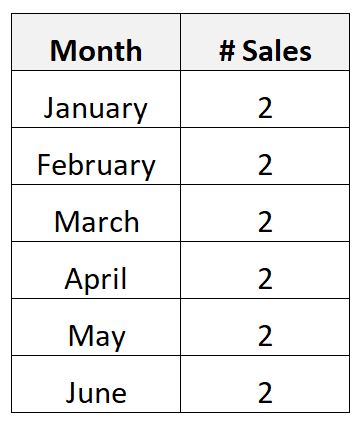
نظرًا لأن المنتج باهظ الثمن للغاية، فقد اتضح أن الشركة تبيع فقط اثنتين فقط شهريًا.
في هذا السيناريو، يبلغ متوسط عدد المنتجات المباعة شهريًا اثنين ويكون الانحراف المعياري للمنتجات الشهرية المباعة صفرًا.
عندما تواجه انحرافًا معياريًا قدره صفر في مجموعة بيانات حقيقية، فاعلم أن هذا يعني أن كل قيمة في مجموعة البيانات هي نفسها تمامًا.
مصادر إضافية
توفر البرامج التعليمية التالية معلومات إضافية حول الانحراف المعياري في الإحصائيات:
ما أهمية الانحراف المعياري؟
الانحراف المعياري والخطأ المعياري: ما الفرق؟
الانحراف المعياري والمدى الربيعي: ما الفرق؟
About Author
دكتور بنيامين أندرسون
مرحبًا، أنا بنجامين، أستاذ الإحصاء المتقاعد الذي تحول إلى مدرس متخصص في Statorials. بفضل خبرتي الواسعة في مجال الإحصاء، فأنا حريص على مشاركة معرفتي لتمكين الطلاب من خلال Statorials. تعرف أكثر