كيفية تنفيذ انحدار ols في بايثون (مع مثال)

يعد انحدار المربعات الصغرى العادية (OLS) طريقة تسمح لنا بالعثور على سطر يصف العلاقة بين واحد أو أكثر من متغيرات التوقع ومتغير الاستجابة .

تتيح لنا هذه الطريقة إيجاد المعادلة التالية:

ŷ = ب ₀ + ب ₁ س

ذهب:

• ŷ : قيمة الاستجابة المقدرة
• ب ₀ : أصل خط الانحدار
• ب ₁ : ميل خط الانحدار

يمكن أن تساعدنا هذه المعادلة في فهم العلاقة بين المتنبئ ومتغير الاستجابة، ويمكن استخدامها للتنبؤ بقيمة متغير الاستجابة بمعلومية قيمة المتغير المتنبئ.

يوضح المثال التالي خطوة بخطوة كيفية إجراء انحدار OLS في Python.

الخطوة 1: إنشاء البيانات

في هذا المثال، سنقوم بإنشاء مجموعة بيانات تحتوي على المتغيرين التاليين لـ 15 طالبًا:

• إجمالي عدد الساعات المدروسة
• نتيجة الإمتحان

سنقوم بإجراء انحدار OLS، باستخدام الساعات كمتغير متوقع ودرجة الامتحان كمتغير الاستجابة.

يوضح الكود التالي كيفية إنشاء مجموعة البيانات المزيفة هذه في الباندا:

 import pandas as pd

#createDataFrame
df = pd. DataFrame ({' hours ': [1, 2, 4, 5, 5, 6, 6, 7, 8, 10, 11, 11, 12, 12, 14],
                   ' score ': [64, 66, 76, 73, 74, 81, 83, 82, 80, 88, 84, 82, 91, 93, 89]})

#view DataFrame
print (df)

    hours score
0 1 64
1 2 66
2 4 76
3 5 73
4 5 74
5 6 81
6 6 83
7 7 82
8 8 80
9 10 88
10 11 84
11 11 82
12 12 91
13 12 93
14 14 89

الخطوة 2: إجراء انحدار OLS

بعد ذلك، يمكننا استخدام الوظائف الموجودة في وحدة statsmodels لإجراء انحدار OLS، باستخدام الساعات كمتغير متوقع والنتيجة كمتغير الاستجابة :

 import statsmodels.api as sm

#define predictor and response variables
y = df[' score ']
x = df[' hours ']

#add constant to predictor variables
x = sm. add_constant (x)

#fit linear regression model
model = sm. OLS (y,x). fit ()

#view model summary
print ( model.summary ())

                            OLS Regression Results                            
==================================================== ============================
Dept. Variable: R-squared score: 0.831
Model: OLS Adj. R-squared: 0.818
Method: Least Squares F-statistic: 63.91
Date: Fri, 26 Aug 2022 Prob (F-statistic): 2.25e-06
Time: 10:42:24 Log-Likelihood: -39,594
No. Observations: 15 AIC: 83.19
Df Residuals: 13 BIC: 84.60
Model: 1                                         
Covariance Type: non-robust                                         
==================================================== ============================
                 coef std err t P>|t| [0.025 0.975]
-------------------------------------------------- ----------------------------
const 65.3340 2.106 31.023 0.000 60.784 69.884
hours 1.9824 0.248 7.995 0.000 1.447 2.518
==================================================== ============================
Omnibus: 4,351 Durbin-Watson: 1,677
Prob(Omnibus): 0.114 Jarque-Bera (JB): 1.329
Skew: 0.092 Prob(JB): 0.515
Kurtosis: 1.554 Cond. No. 19.2
==================================================== ============================

من عمود coef يمكننا رؤية معاملات الانحدار وكتابة معادلة الانحدار المجهزة التالية:

النتيجة = 65.334 + 1.9824*(ساعات)

وهذا يعني أن كل ساعة إضافية تتم دراستها ترتبط بزيادة في متوسط درجات الامتحان بمقدار 1.9824 نقطة.

تخبرنا القيمة الأصلية البالغة 65,334 بمتوسط درجات الاختبار المتوقعة للطالب الذي يدرس لمدة صفر ساعة.

يمكننا أيضًا استخدام هذه المعادلة للعثور على درجة الامتحان المتوقعة بناءً على عدد الساعات التي يدرسها الطالب.

على سبيل المثال، الطالب الذي يدرس لمدة 10 ساعات يجب أن يحقق درجة الامتحان 85.158 :

النتيجة = 65.334 + 1.9824*(10) = 85.158

فيما يلي كيفية تفسير بقية ملخص النموذج:

• P(>|t|): هذه هي القيمة p المرتبطة بمعاملات النموذج. وبما أن القيمة p للساعات (0.000) أقل من 0.05، يمكننا القول أن هناك علاقة ذات دلالة إحصائية بين الساعات والنتيجة .
• R-squared: يخبرنا هذا أن نسبة التباين في درجات الامتحان يمكن تفسيرها بعدد الساعات المدروسة. في هذه الحالة، يمكن تفسير 83.1% من التباين في الدرجات من خلال ساعات الدراسة.
• إحصائية F وقيمة p: تخبرنا إحصائية F ( 63.91 ) والقيمة p المقابلة لها ( 2.25e-06 ) بالأهمية الإجمالية لنموذج الانحدار، أي ما إذا كانت المتغيرات المتوقعة في النموذج مفيدة في تفسير التباين. في متغير الاستجابة نظرًا لأن القيمة p في هذا المثال أقل من 0.05، فإن نموذجنا ذو دلالة إحصائية وتعتبر الساعات مفيدة في شرح تباين النتيجة .

الخطوة 3: تصور الخط الأنسب

أخيرًا، يمكننا استخدام حزمة تصور بيانات matplotlib لتصور خط الانحدار الملائم لنقاط البيانات الفعلية:

 import matplotlib. pyplot as plt

#find line of best fit
a, b = np. polyfit (df[' hours '], df[' score '], 1 )

#add points to plot
plt. scatter (df[' hours '], df[' score '], color=' purple ')

#add line of best fit to plot
plt. plot (df[' hours '], a*df[' hours ']+b)

#add fitted regression equation to plot
plt. text ( 1 , 90 , 'y = ' + '{:.3f}'.format(b) + ' + {:.3f}'.format(a) + 'x', size= 12 )

#add axis labels
plt. xlabel (' Hours Studied ')
plt. ylabel (' Exam Score ')

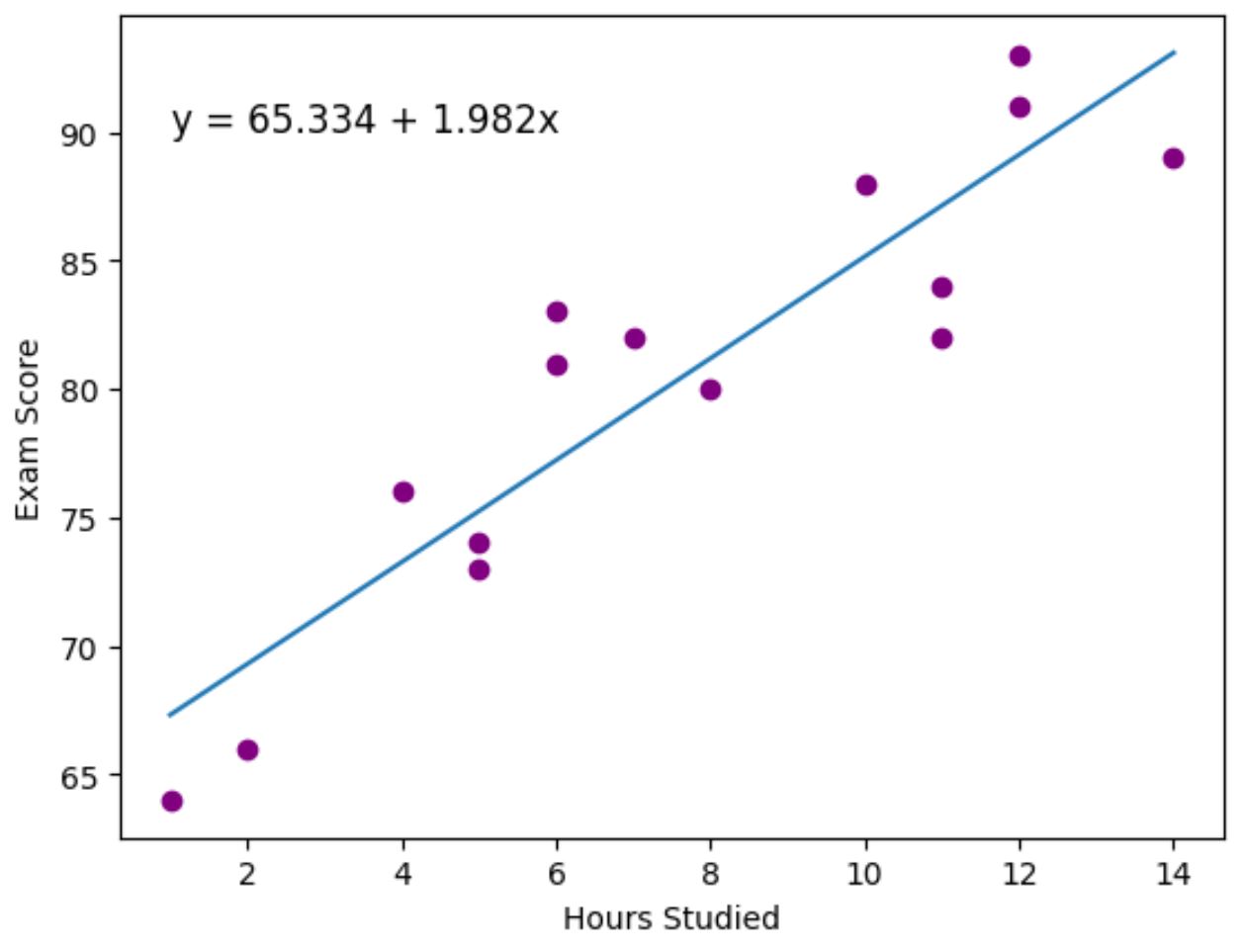
تمثل النقاط الأرجوانية نقاط البيانات الفعلية ويمثل الخط الأزرق خط الانحدار المجهز.

استخدمنا أيضًا الدالة plt.text() لإضافة معادلة الانحدار المجهزة إلى الزاوية اليسرى العليا من المخطط.

وبالنظر إلى الرسم البياني، يبدو أن خط الانحدار الملائم يجسد العلاقة بين متغير الساعات ومتغير النتيجة بشكل جيد.

مصادر إضافية

تشرح البرامج التعليمية التالية كيفية تنفيذ المهام الشائعة الأخرى في بايثون:

كيفية تنفيذ الانحدار اللوجستي في بايثون
كيفية تنفيذ الانحدار الأسي في بايثون
كيفية حساب AIC لنماذج الانحدار في بايثون