نظرية الحد المركزي

تشرح هذه المقالة ماهية نظرية الحد المركزي (CLT) وفيما يتم استخدامها في الإحصاء. ستجد أيضًا ما هي صيغة نظرية الحد المركزي ومثال لتطبيقها خطوة بخطوة.

ما هي نظرية الحد المركزي؟

في الإحصاء، تنص نظرية الحد المركزي ، والتي تسمى أيضًا نظرية الحد المركزي ، على أن توزيع متوسطات العينة يقترب من التوزيع الطبيعي مع زيادة حجم العينة، بغض النظر عن التوزيع الاحتمالي للسكان.

أي أن نظرية الحد المركزي تنص على أنه إذا أخذنا عددًا كبيرًا بما فيه الكفاية من العينات، فيمكن تقريب متوسط تلك العينات إلى التوزيع الطبيعي.

بالإضافة إلى ذلك، تنص نظرية الحد المركزي على أن متوسط العينة سيقترب من قيمة متوسط المجتمع مع زيادة حجم العينة. وهذا يسمح لنا بتقريب معايير السكان الإحصائيين. أدناه سنرى كيف يتم ذلك.

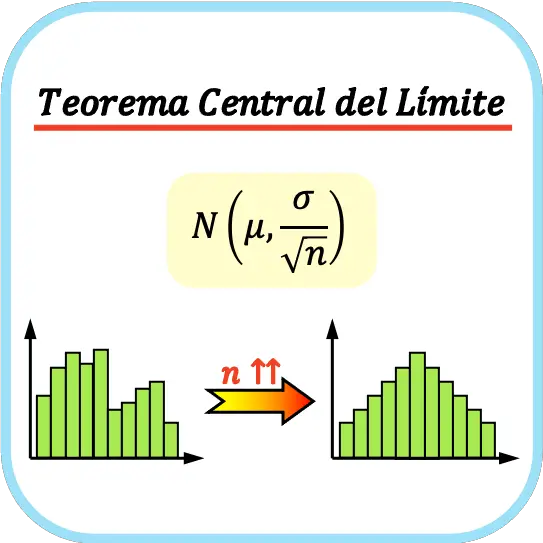
وبشكل عام يعتبر أنه لتطبيق نظرية الحد المركزي يجب أن لا يقل حجم العينة عن 30 ملاحظة، على الرغم من أن ذلك يعتمد على خصائص المتغير المدروس.

نظرية الحد المركزي لها العديد من التطبيقات، حيث أن التوزيع الطبيعي يسمح بإجراء حسابات إحصائية استنتاجية، مثل اختبار الفرضيات أو فترات الثقة. على سبيل المثال، في مجال التمويل، يتم استخدام نظرية الحد المركزي لتحليل العائد والمخاطر للاستثمار.

مثال على نظرية الحد المركزي

بعد أن رأينا تعريف نظرية الحد المركزي، دعونا نلقي نظرة على مثال لفهم معناها بشكل كامل.

مثال على نظرية الحد المركزي هو رمي حجر النرد. تتبع لفة القالب توزيعًا موحدًا منفصلاً ، نظرًا لأن جميع النتائج متساوية الاحتمال. لكن توزيع مجموع عدة نتائج يقترب من التوزيع الطبيعي.

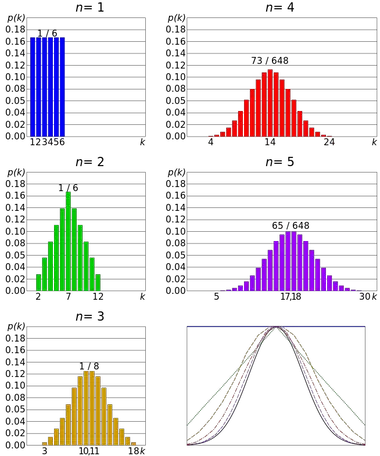
وبالتالي، كلما زاد عدد الرميات، زاد احتمال أن يميل شكل توزيع الوسائل إلى التشابه مع الرسم البياني للتوزيع الطبيعي.

صيغة نظرية الحد المركزي

تنص نظرية الحد المركزي على أنه إذا كان عدد السكان لديه متوسط μ وانحراف معياري σ وأخذنا عددًا كبيرًا بما فيه الكفاية من العينات (n≥30)، فيمكن تقريب مجموعة متوسطات العينة إلى التوزيع الطبيعي بمتوسط μ وانحراف معياري σ /√ن.

علاوة على ذلك ، _{إذا كان} X _{1 ،} إلى توزيع طبيعي محدد بالصيغة التالية:

حل تمرين على نظرية الحد المركزي

لكي تتمكن من استيعاب المفهوم بشكل كامل، إليك تمرينًا تم حله لنظرية الحد المركزي.

• تبيع إحدى الشركات الأجزاء التي تستخدم لاستبدال بعض مكونات الألعاب. العملة المعدنية يبلغ متوسط وزنها 300 جرام وانحرافها المعياري 50 جرامًا. إذا طلب العميل دفعة مكونة من 100 قطعة، ما هو احتمال أن يكون متوسط وزن القطع في الدفعة أكبر من 305 جم؟ وما هو احتمال أن يكون وزن مجموعة مكونة من 100 قطعة أكثر من 31 كجم؟

وبما أن حجم الدفعة كبير (n=100)، فيمكننا تطبيق نظرية الحد المركزي لحل المشكلة.

وبالتالي، باستخدام صيغة نظرية الحد المركزي، يمكن تقريب توزيع متوسطات العينة إلى التوزيع الطبيعي باستخدام المعلمات التالية:

نجري الآن عملية الكتابة حتى نتمكن بعد ذلك من إيجاد الاحتمال الذي يطلب منا التمرين الحصول عليه. للقيام بذلك، نحن بحاجة إلى طرح المتوسط من التوزيع ثم القسمة على الانحراف المعياري:

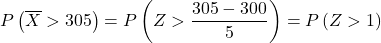وبالتالي، لإيجاد احتمال أن يكون متوسط وزن القطع في الدفعة أكبر من 305 جم، يجب أن ننظر إلى القيمة التي تتوافق معها Z>1 في جدول التوزيع الطبيعي :

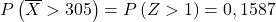من ناحية أخرى، وبفضل نظرية الحد المركزي، يمكننا أن نعرف أن مجموعة مكونة من 100 قطعة نقدية يمكن أن تقترب من التوزيع الطبيعي، حيث أن جميع العملات المعدنية تتبع نفس التوزيع. لذلك، لتحديد احتمال أن يكون وزن مجموعة مكونة من 100 قطعة نقدية أكثر من 31 كجم، يجب علينا تطبيق الصيغة الأخرى لنظرية الحد المركزي:

لذلك نعيد عملية الكتابة، ثم نجد الاحتمال الثاني الذي تطرحه علينا المشكلة:

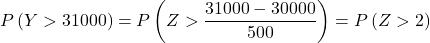أخيرًا، يمكننا تحديد احتمال أن يزيد وزن الدفعة المكونة من 100 قطعة عن 31 كجم باستخدام جدول التوزيع الطبيعي:

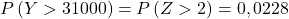➤ انظر: قانون الأعداد الكبيرة