كيفية إجراء اختبار cramer-von mises في لغة r (مع أمثلة)
يتم استخدام اختبار Cramer-Von Mises لتحديد ما إذا كانت العينة تأتي من التوزيع الطبيعي أم لا.
يعد هذا النوع من الاختبارات مفيدًا لتحديد ما إذا كانت مجموعة بيانات معينة تأتي من التوزيع الطبيعي أم لا، وهو افتراض شائع الاستخدام في العديد من الاختبارات الإحصائية، بما في ذلك الانحدار ، و ANOVA ، واختبارات T ، وغيرها الكثير. ‘آحرون.
يمكننا بسهولة إجراء اختبار Cramer-Von Mises باستخدام الدالة cvm.test() من الحزمة goftest في R.
يوضح المثال التالي كيفية استخدام هذه الوظيفة عمليًا.
مثال 1: اختبار كرامر فون ميزس على البيانات العادية
يوضح التعليمة البرمجية التالية كيفية إجراء اختبار Cramer-Von Mises على مجموعة بيانات بحجم العينة n=100:
library (goftest) #make this example reproducible set. seeds (0) #create dataset of 100 random values generated from a normal distribution data <- rnorm(100) #perform Cramer-Von Mises test for normality cvm. test (data, ' pnorm ') Cramer-von Mises test of goodness-of-fit Null hypothesis: Normal distribution Parameters assumed to be fixed data:data omega2 = 0.078666, p-value = 0.7007
وتبين أن القيمة p للاختبار هي 0.7007 .
وبما أن هذه القيمة لا تقل عن 0.05، يمكننا أن نفترض أن بيانات العينة تأتي من مجتمع موزع بشكل طبيعي.
لا ينبغي أن تكون هذه النتيجة مفاجئة لأننا أنشأنا بيانات العينة باستخدام الدالة rnorm() ، التي تولد قيمًا عشوائية من التوزيع الطبيعي القياسي .
ذات صلة: دليل إلى dnorm وpnorm وqnorm وrnorm في R
يمكننا أيضًا إنتاج رسم بياني للتحقق بصريًا من توزيع بيانات العينة بشكل طبيعي:
hist(data, col=' steelblue ')
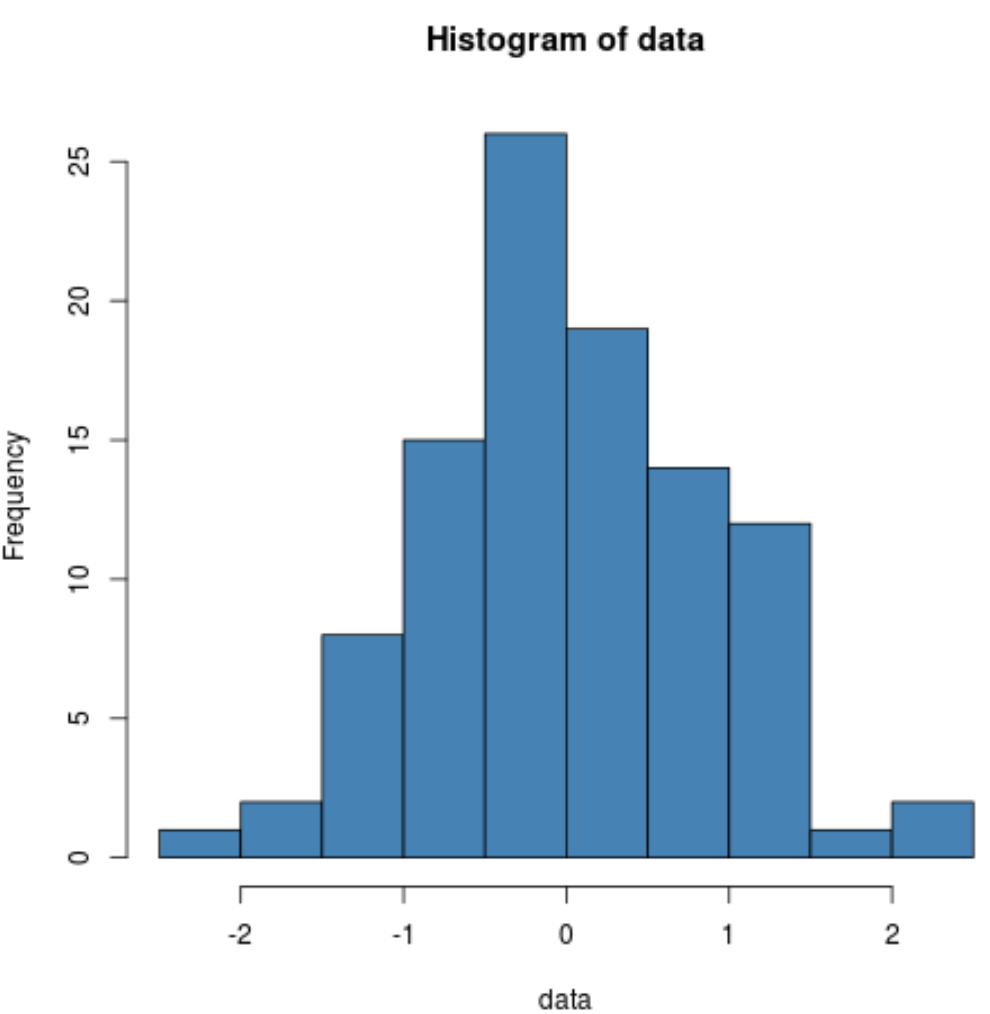
يمكننا أن نرى أن التوزيع على شكل جرس تمامًا مع وجود قمة في مركز التوزيع، وهو أمر نموذجي للبيانات الموزعة بشكل طبيعي.
مثال 2: اختبار Cramer-Von Mises على البيانات غير العادية
يوضح الكود التالي كيفية إجراء اختبار Cramer-Von Mises على مجموعة بيانات بحجم عينة 100 حيث يتم إنشاء القيم بشكل عشوائي من توزيع بواسون :
library (goftest) #make this example reproducible set. seeds (0) #create dataset of 100 random values generated from a Poisson distribution data <- rpois(n=100, lambda=3) #perform Cramer-Von Mises test for normality cvm. test (data, ' pnorm ') Cramer-von Mises test of goodness-of-fit Null hypothesis: Normal distribution Parameters assumed to be fixed data:data omega2 = 27.96, p-value < 2.2e-16
تبين أن القيمة p للاختبار منخفضة للغاية.
وبما أن هذه القيمة أقل من 0.05، فلدينا أدلة كافية للقول بأن بيانات العينة لا تأتي من مجموعة سكانية موزعة بشكل طبيعي.
لا ينبغي أن تكون هذه النتيجة مفاجئة لأننا أنشأنا بيانات العينة باستخدام الدالة rpois() ، التي تولد قيمًا عشوائية من توزيع بواسون.
ذات صلة: دليل إلى dpois وppois وqpois وrpois في R
يمكننا أيضًا إنتاج رسم بياني لنرى بصريًا أن بيانات العينة لا يتم توزيعها بشكل طبيعي:
hist(data, col=' coral2 ')
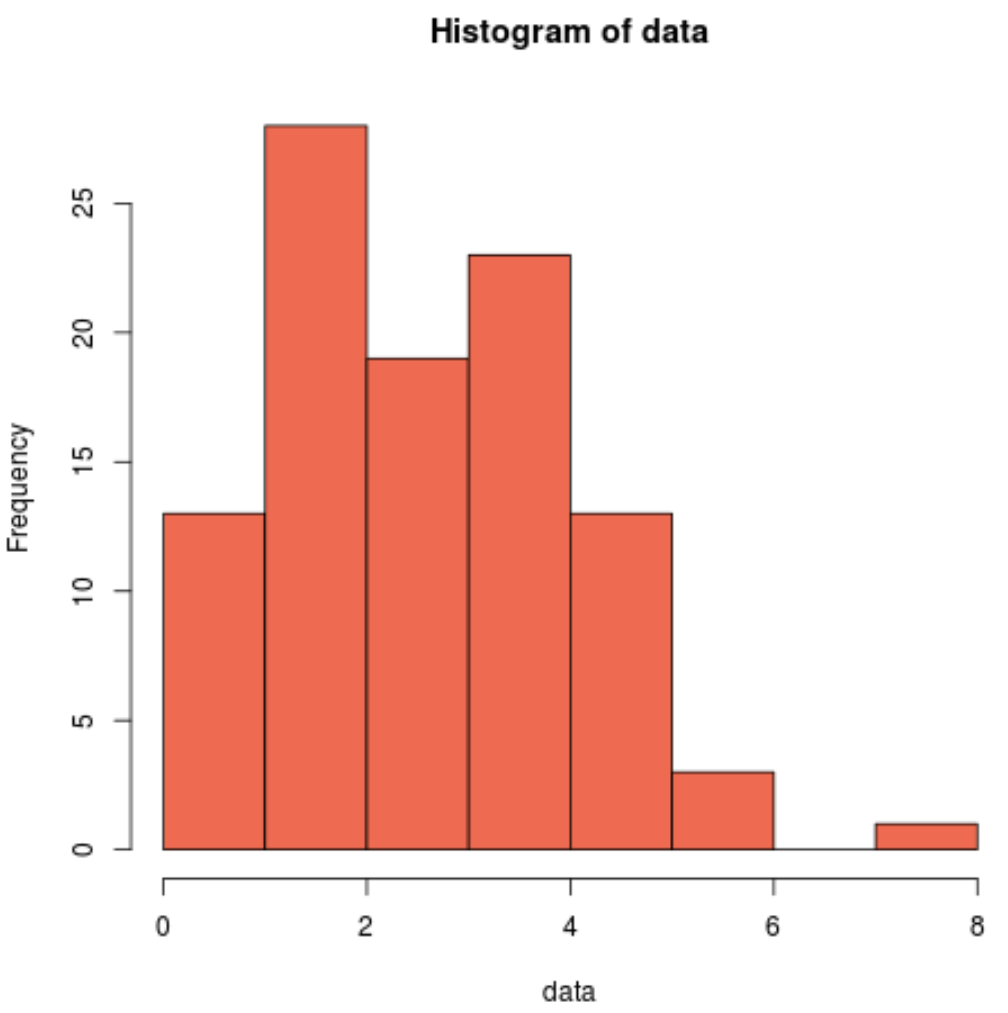
يمكننا أن نرى أن التوزيع منحرف إلى اليمين وليس له “شكل الجرس” النموذجي المرتبط بالتوزيع الطبيعي.
وبالتالي، فإن الرسم البياني الخاص بنا يطابق نتائج اختبار Cramer-Von Mises ويؤكد أن بيانات العينة لدينا لا تأتي من التوزيع الطبيعي.
ما يجب القيام به مع البيانات غير العادية
إذا لم يتم توزيع مجموعة بيانات معينة بشكل طبيعي، فيمكننا غالبًا إجراء أحد التحويلات التالية لجعلها أكثر طبيعية:
1. تحويل السجل: تحويل متغير الاستجابة من y إلى log(y) .
2. تحويل الجذر التربيعي: تحويل متغير الاستجابة من y إلى √y .
3. تحويل الجذر التكعيبي: تحويل متغير الاستجابة من y إلى y 1/3 .
ومن خلال إجراء هذه التحويلات، يقترب متغير الاستجابة بشكل عام من التوزيع الطبيعي.
ارجع إلى هذا البرنامج التعليمي لمعرفة كيفية إجراء هذه التحولات عمليًا.
مصادر إضافية
تشرح البرامج التعليمية التالية كيفية إجراء اختبارات الحالة الطبيعية الأخرى في R:
كيفية إجراء اختبار شابيرو ويلك في R
كيفية إجراء اختبار أندرسون-دارلينج في R
كيفية إجراء اختبار Kolmogorov-Smirnov في R