كيفية إجراء اختبار t مع التباينات غير المتكافئة في إكسيل
يتم استخدام اختبار t المكون من عينتين لتحديد ما إذا كانت متوسطات مجتمعين متساويتين أم لا.
هناك إصداران من مثالين لاختبار t يمكنك استخدامهما:
- اختبار t مع تباينات متساوية
- اختبار t مع تباينات غير متساوية
نستخدم اختبار t مع تباينات غير متساوية عندما تكون تباينات العينتين غير متساوية.
إن أبسط طريقة لتحديد ما إذا كانت الفروق بين العينتين متساوية هي استخدام قاعدة التباين الأساسية .
كقاعدة عامة، إذا كانت نسبة التباين الأكبر إلى أصغر التباين أقل من 4، فيمكننا أن نفترض أن التباينات متساوية تقريبًا.
وبخلاف ذلك، إذا كانت النسبة تساوي أو أكبر من 4، فمن المفترض أن التباينات غير متساوية.
يوضح المثال التالي خطوة بخطوة كيفية إجراء اختبار t لعينتين مع تباينات غير متساوية في Excel.
الخطوة 1: أدخل البيانات
لنفترض أننا نريد تحديد ما إذا كانت طريقتان مختلفتان للدراسة تؤديان إلى متوسط درجات اختبار مختلفة بين الطلاب في جامعة معينة.
نقوم باختيار عينة عشوائية مكونة من 20 طالبًا لاستخدام كل طريقة دراسية وتسجيل نتائج امتحاناتهم:
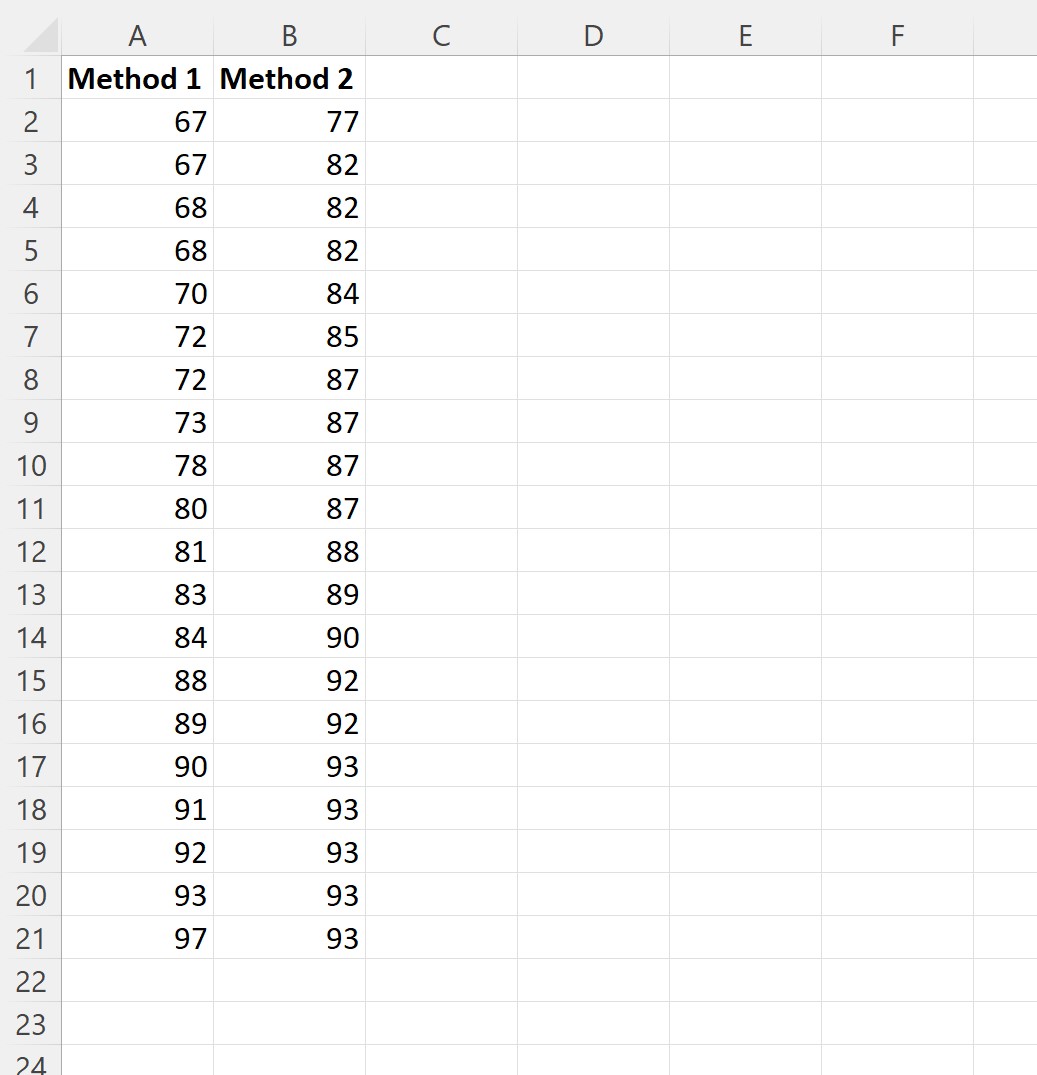
الخطوة الثانية: تحديد التباين المتساوي أو غير المتساوي
ثم يمكننا حساب نسبة تباينات العينة:
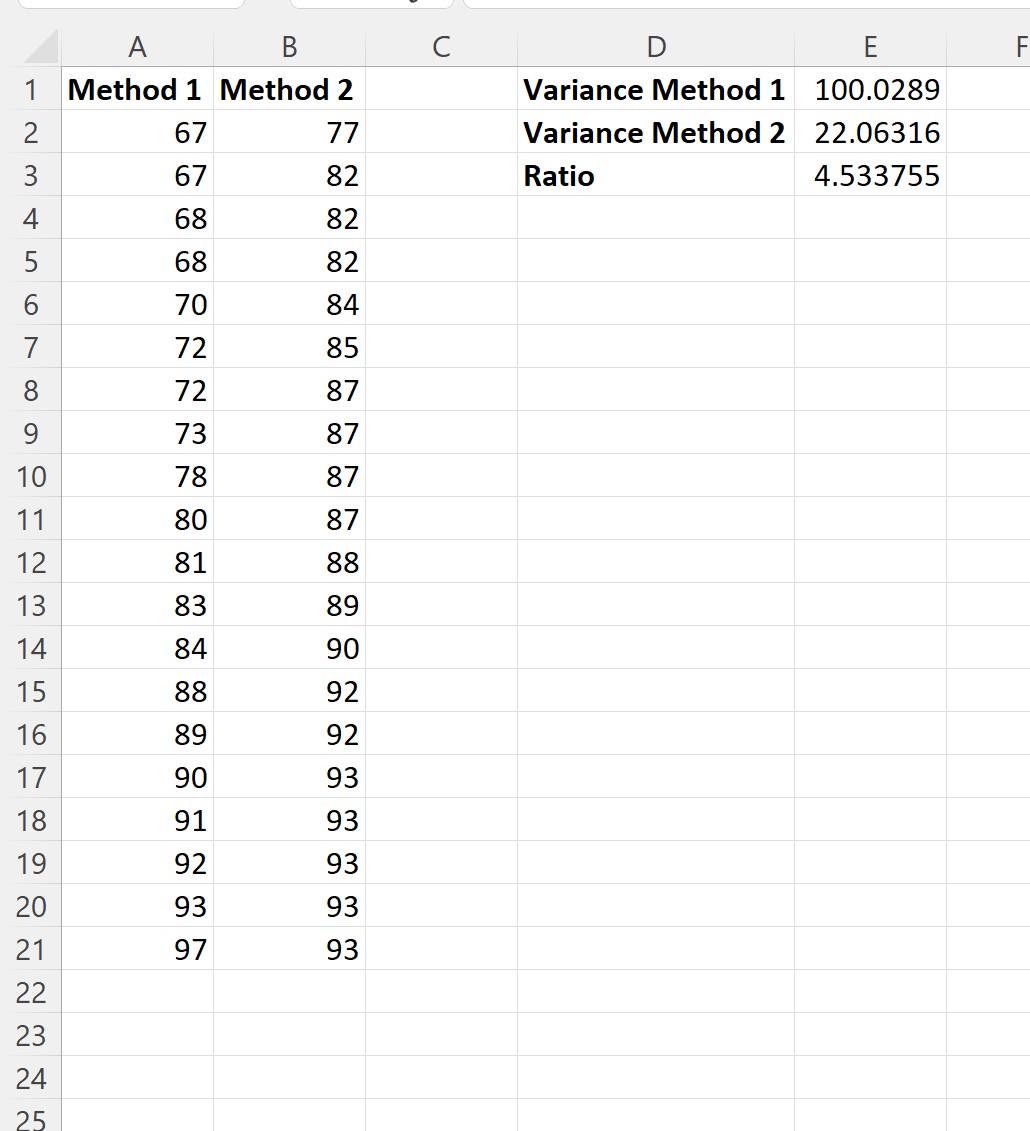
فيما يلي الصيغ التي كتبناها في كل خلية:
- الخلية E1: =VAR.S(A2:A21)
- الخلية E2: =VAR.S(B2:B21)
- الخلية E3: =E1/E2
يمكننا أن نرى أن نسبة أكبر تباين في العينة إلى أصغر تباين في العينة هو 4.533755 .
وبما أن هذه القيمة أكبر من أو تساوي 4، فإننا نفترض أن التباينات بين العينتين غير متساوية.
الخطوة 3: إجراء اختبار t لعينتين مع تباين غير متساوي
بعد ذلك، يمكننا إجراء اختبار t لعينتين مع تباينات غير متساوية لتحديد ما إذا كان متوسط درجات الاختبار بين العينتين متساويًا.
للقيام بذلك، انقر فوق علامة التبويب “البيانات” في الشريط العلوي، ثم انقر فوق الزر “تحليل البيانات” في المجموعة “تحليل” :

إذا كنت لا ترى هذا الزر، فستحتاج أولاً إلى تثبيت حزمة أدوات تحليل البيانات المجانية في Excel .
في النافذة الجديدة التي تظهر، انقر فوق اختبار T: نموذجان يفترضان تباينات غير متساوية ، ثم انقر فوق موافق :
في النافذة الجديدة التي تظهر، املأ المعلومات التالية، ثم انقر فوق “موافق” :
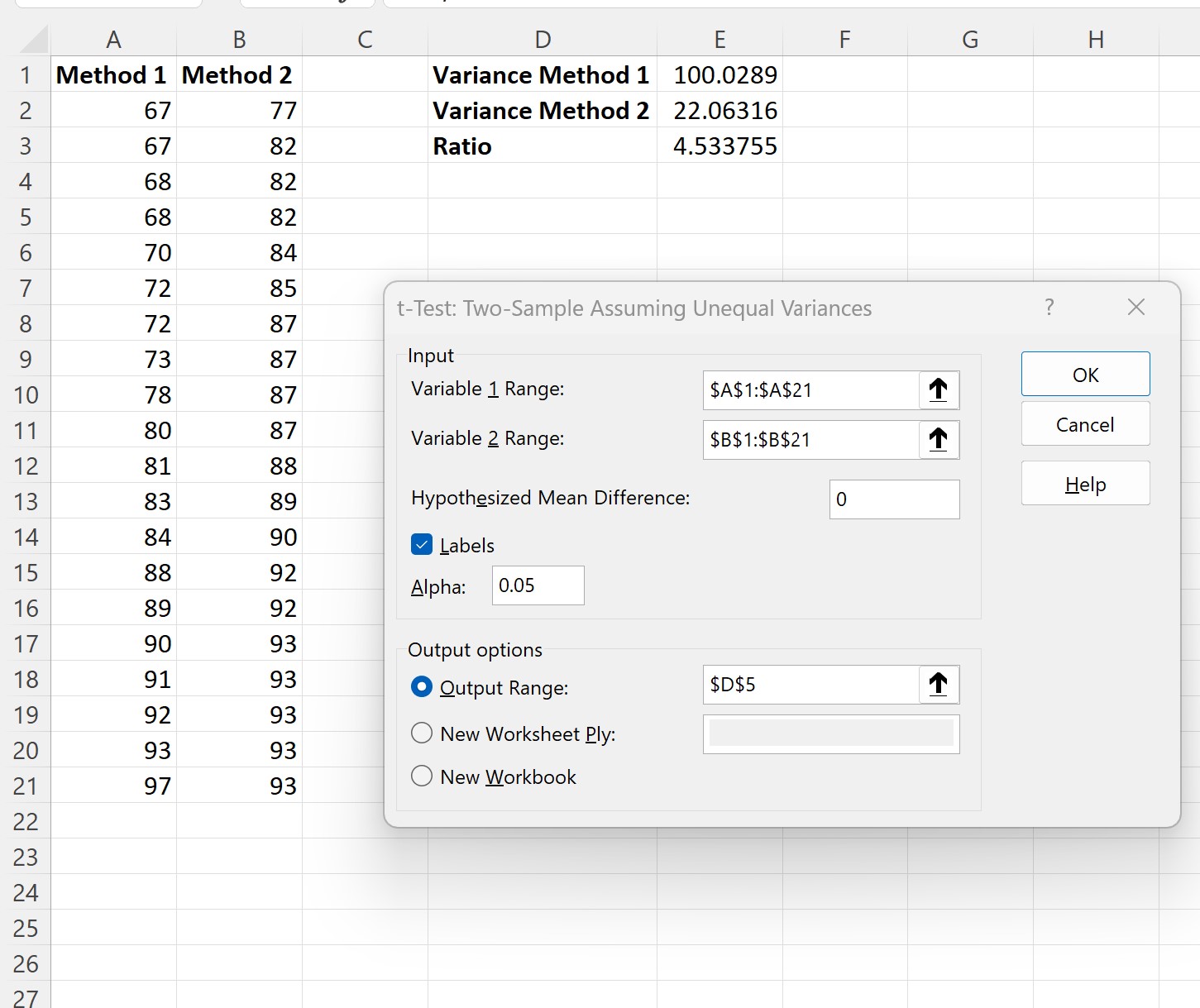
بمجرد النقر فوق “موافق” ، ستظهر نتائج المثالين لاختبار t:
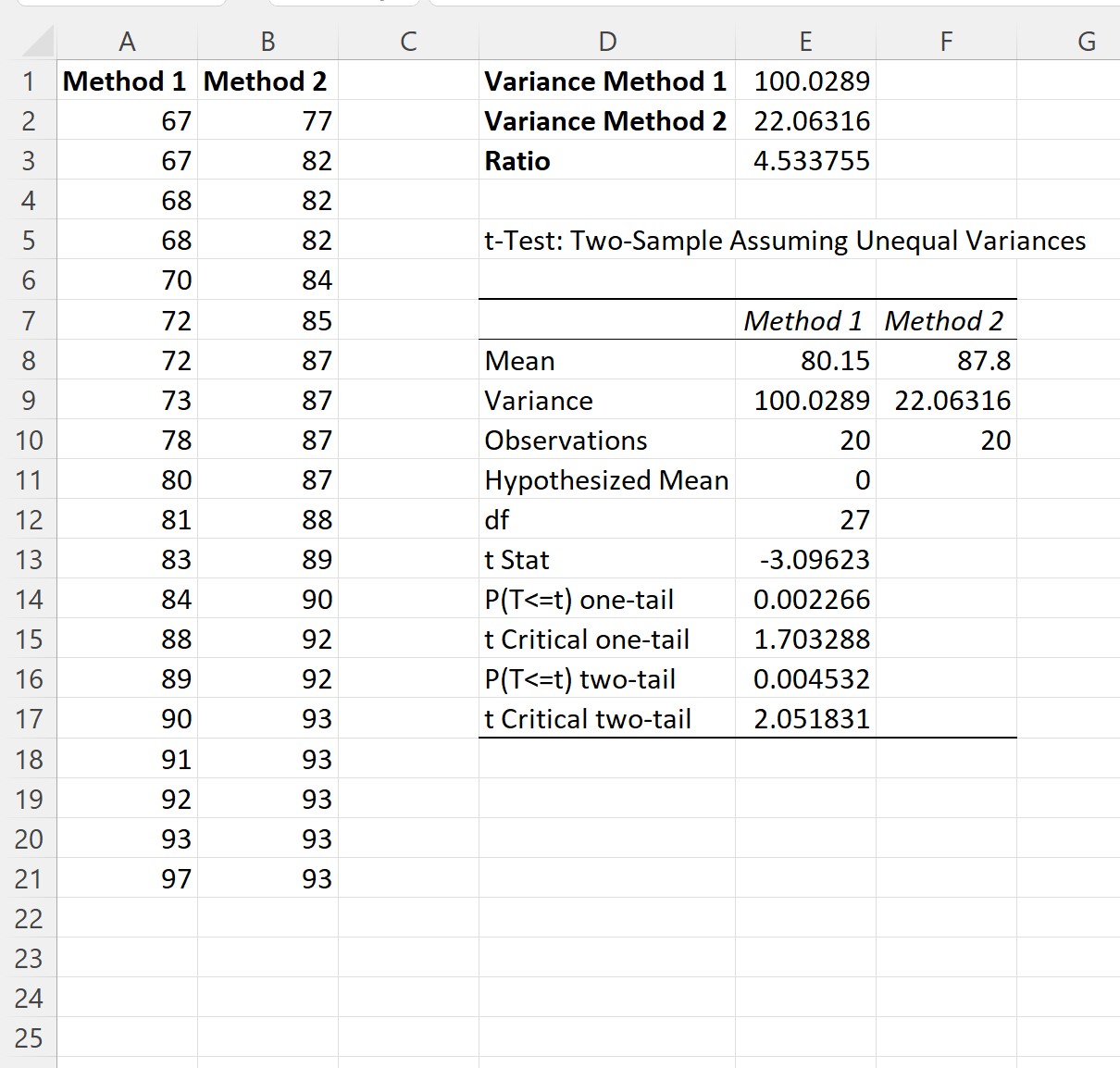
الخطوة 4: تفسير النتائج
ومن النتيجة يمكننا أن نرى:
- وكان متوسط درجة الامتحان للطريقة الأولى 80.15 .
- وكان متوسط درجة الامتحان للطريقة الثانية 87.8 .
- وكانت إحصائية اختبار t -3.09623 .
- وكانت القيمة p المقابلة ذات الذيل 0.004532 .
وبما أن هذه القيمة p أقل من 0.05، يمكننا أن نستنتج أن هناك فرق ذو دلالة إحصائية في متوسط درجات الامتحان بين طريقتي الدراسة.
مصادر إضافية
تشرح البرامج التعليمية التالية كيفية تنفيذ المهام الشائعة الأخرى في Excel:
كيفية إجراء اختبار t لعينة واحدة في Excel
كيفية إجراء اختبار t للعينات المقترنة في Excel
كيفية إجراء عينة واحدة وعينتين من اختبارات Z في Excel