كيفية إجراء اختبار ليفين في sas
تفترض العديد من الاختبارات الإحصائية (مثل تحليل التباين أحادي الاتجاه ) أن التباين بين المجموعات المتعددة متساوٍ.
إحدى طرق اختبار هذه الفرضية رسميًا هي استخدام اختبار ليفين ، الذي يختبر ما إذا كان التباين بين مجموعتين أو أكثر متساويًا أم لا.
يستخدم هذا الاختبارالافتراضات التالية:
- الفرضية الصفرية ( H0 ) : التباين بين المجموعات متساوي.
- الفرضية البديلة ( HA ) : التباين بين المجموعات غير متساوي.
إذا كانت القيمة p للاختبار أقل من مستوى الأهمية المختار، فيمكننا رفض فرضية العدم ونستنتج أن لدينا أدلة كافية للقول بأن التباين بين المجموعات غير متساوٍ.
يوضح المثال التالي كيفية إجراء اختبار ليفين في SAS.
مثال: اختبار ليفين في SAS
لنفترض أن لدينا مجموعة البيانات التالية في SAS والتي توضح الأسمدة المستخدمة في النباتات المختلفة والنمو الناتج (بالبوصة) لـ 18 نباتًا:
/*create dataset*/ data my_data; input fertilizer $growth; datalines ; At 29 At 23 At 20 At 21 At 33 At 30 B 19 B 19 B17 B24 B25 B29 C 21 C22 C 30 C25 C24 C 33 ; run ; /*view dataset*/ proc print data =my_data;
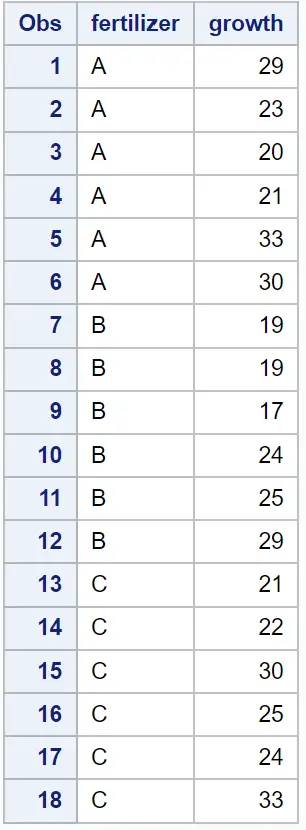
لنفترض أننا نريد إجراء تحليل التباين (ANOVA) أحادي الاتجاه لتحديد ما إذا كان متوسط نمو النبات متساويًا بين الأسمدة الثلاثة المختلفة.
يمكننا استخدام الصيغة التالية في SAS لإجراء تحليل ANOVA أحادي الاتجاه باستخدام العبارة hovtest=levene(type=abs) لإجراء اختبار Levene أيضًا لتحديد ما إذا كانت المجموعات الثلاث لها تباينات متساوية أم لا:
/*perform one-way ANOVA along with Levene's test*/
proc glm data = my_data;
class fertilizer;
model growth = fertilizer;
means fertilizer / hovtest =levene(type=abs);
run ;
جدول النتائج الأول يوضح نتائج تحليل التباين الأحادي:
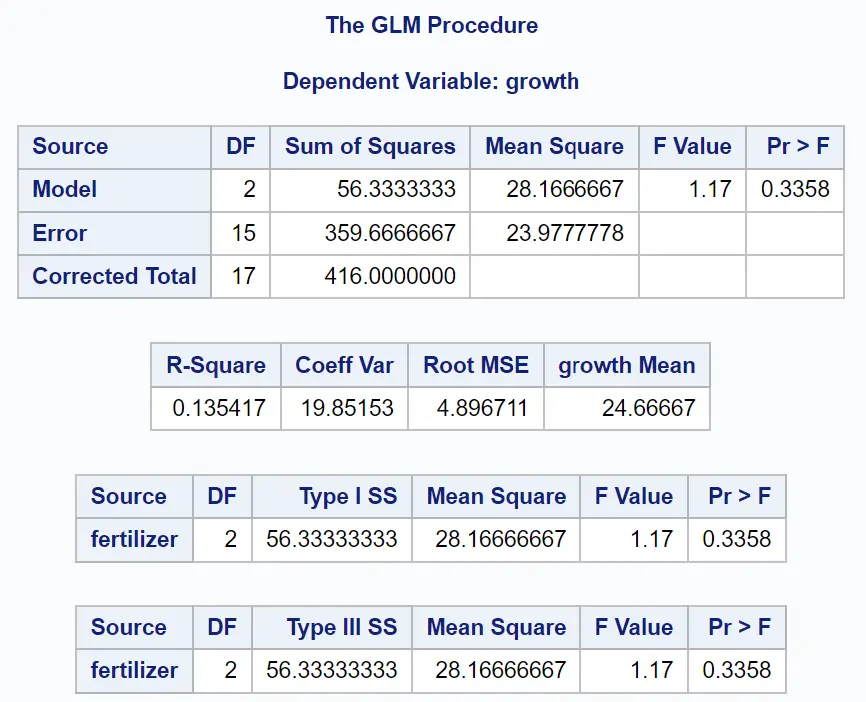
القيمة p في جدول ANOVA هي 0.3358 .
وبما أن هذه القيمة لا تقل عن 0.05 فإننا نستنتج أنه لا يوجد فرق ذو دلالة إحصائية في متوسط نمو النبات بين الأسمدة الثلاثة.
ذات صلة: كيفية تفسير قيمة F وقيمة P في ANOVA
للتأكد من موثوقية هذه النتيجة، يجب علينا التحقق من التحقق من افتراض مساواة التباينات.
يمكننا أن نرى نتيجة اختبار ليفين في الجدول الثاني للمخرجات:

من هذا الجدول، يمكننا أن نرى أن القيمة الاحتمالية لاختبار ليفين هي 0.6745 .
وبما أن هذه القيمة لا تقل عن 0.05، فإننا نفشل في رفض الفرضية الصفرية للاختبار.
بمعنى آخر، يمكننا أن نفترض أن المجموعات الثلاث لها تباينات متساوية.
ملاحظة : استخدمنا الوسيطة type=abs في الدالة levene() لتحديد أنه يجب علينا استخدام القيمة المطلقة للقيم المتبقية عند تشغيل اختبار Levene. وهذا يتوافق مع الطريقة التي تستخدمها البرامج الإحصائية الأخرى مثل R.
مصادر إضافية
تشرح البرامج التعليمية التالية كيفية إجراء اختبارات إحصائية شائعة أخرى في SAS:
كيفية إجراء اختبار شابيرو ويلك في SAS
كيفية إجراء اختبار كولموجوروف-سميرنوف في SAS
كيفية استخدام Proc Univariate لاختبار الحالة الطبيعية في SAS