كيفية التحقق من افتراضات anova

ANOVA أحادي الاتجاه هو اختبار إحصائي يستخدم لتحديد ما إذا كان هناك فرق كبير بين متوسطات ثلاث مجموعات مستقلة أو أكثر أم لا.

فيما يلي مثال على متى يمكننا استخدام ANOVA أحادي الاتجاه:

قمت بتقسيم فصل مكون من 90 طالبًا بشكل عشوائي إلى ثلاث مجموعات مكونة من 30 طالبًا. تستخدم كل مجموعة أسلوب دراسة مختلفًا لمدة شهر للتحضير للامتحان. وفي نهاية الشهر، يؤدي جميع الطلاب نفس الاختبار.

تريد معرفة ما إذا كان أسلوب الدراسة له تأثير على درجات الامتحانات أم لا. لذا، عليك إجراء تحليل التباين (ANOVA) أحادي الاتجاه لتحديد ما إذا كان هناك فرق ذو دلالة إحصائية بين متوسط درجات المجموعات الثلاث.

قبل أن نتمكن من إجراء تحليل التباين أحادي الاتجاه، يجب علينا أولاً التحقق من استيفاء ثلاثة افتراضات.

1. الحالة الطبيعية – تم أخذ كل عينة من مجتمع موزع بشكل طبيعي.

2. التباينات المتساوية – تباينات المجتمعات التي تم سحب العينات منها متساوية.

3. الاستقلال – الملاحظات داخل كل مجموعة مستقلة عن بعضها البعض وتم الحصول على الملاحظات داخل المجموعات عن طريق أخذ عينات عشوائية.

إذا لم يتم استيفاء هذه الافتراضات، فإن نتائج تحليل التباين الأحادي قد لا تكون موثوقة.

وفي هذا المقال نوضح كيفية التحقق من هذه الافتراضات وماذا تفعل إذا تم انتهاك أي منها.

الافتراض رقم 1: الحالة الطبيعية

تفترض ANOVA أن كل عينة تم سحبها من مجتمع موزع بشكل طبيعي.

كيفية التحقق من هذه الفرضية في R:

للتحقق من هذه الفرضية يمكننا استخدام طريقتين:

• تحقق بصريًا من الفرضية باستخدام الرسوم البيانية أو مؤامرات QQ .
• تحقق من الفرضية باستخدام الاختبارات الإحصائية الرسمية مثل Shapiro-Wilk، أو Kolmogorov-Smironov، أو Jarque-Barre، أو D’Agostino-Pearson.

على سبيل المثال، لنفترض أننا قمنا بتوظيف 90 شخصًا للمشاركة في تجربة لإنقاص الوزن حيث قمنا بتعيين 30 شخصًا بشكل عشوائي لمتابعة البرنامج أ أو البرنامج ب أو البرنامج ج لمدة شهر واحد. لمعرفة ما إذا كان للبرنامج تأثير على فقدان الوزن، نريد إجراء تحليل التباين (ANOVA) أحادي الاتجاه. يوضح التعليمة البرمجية التالية كيفية التحقق من افتراض الحالة الطبيعية باستخدام الرسوم البيانية، ومؤامرات QQ، واختبار شابيرو ويلك.

1. تناسب نموذج ANOVA.

 #make this example reproducible
set.seed(0)

#create data frame
data <- data. frame (program = rep(c(" A ", " B ", " C "), each = 30 ),
                   weight_loss = c(runif(30, 0, 3),
                                   runif(30, 0, 5),
                                   runif(30, 1, 7)))

#fit the one-way ANOVA model
model <- aov(weight_loss ~ program, data = data)

2. قم بإنشاء رسم بياني لقيم الاستجابة.

 #create histogram
hist(data$weight_loss)

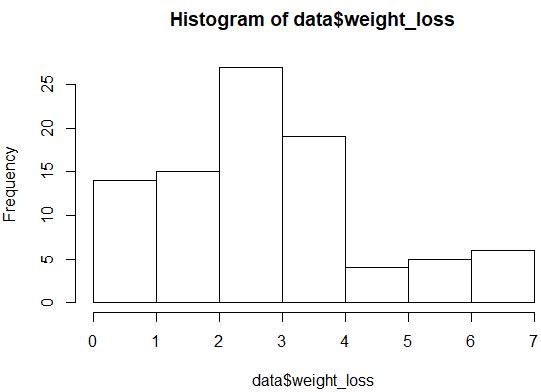
لا يبدو التوزيع موزعًا بشكل طبيعي جدًا (على سبيل المثال، ليس على شكل “جرس”)، ولكن يمكننا أيضًا إنشاء مخطط QQ لإلقاء نظرة أخرى على التوزيع.

3. قم بإنشاء مخطط QQ للبقايا

 #create QQ plot to compare this dataset to a theoretical normal distribution
qqnorm(model$residuals)

#add straight diagonal line to plot
qqline(model$residuals) 

بشكل عام، إذا كانت نقاط البيانات تقع على طول خط قطري مستقيم في مخطط QQ، فمن المرجح أن تتبع مجموعة البيانات التوزيع الطبيعي. في هذه الحالة، يمكننا أن نرى أن هناك انحرافًا ملحوظًا عن الخط على طول الأطراف، مما قد يشير إلى أن البيانات لا يتم توزيعها بشكل طبيعي.

4. إجراء اختبار شابيرو ويلك للحياة الطبيعية.

 #Conduct Shapiro-Wilk Test for normality
shapiro. test (data$weight_loss)

#Shapiro-Wilk normality test
#
#data: data$weight_loss
#W = 0.9587, p-value = 0.005999

يختبر اختبار شابيرو ويلك الفرضية الصفرية القائلة بأن العينات تأتي من التوزيع الطبيعي مقابل الفرضية البديلة القائلة بأن العينات لا تأتي من التوزيع الطبيعي. في هذه الحالة، تكون القيمة p للاختبار هي 0.005999 ، وهي أقل من مستوى ألفا البالغ 0.05. وهذا يشير إلى أن العينات لا تتبع التوزيع الطبيعي.

ماذا تفعل إذا لم يتم احترام هذا الافتراض:

بشكل عام، يعتبر تحليل التباين أحادي الاتجاه قويًا جدًا ضد انتهاكات الافتراض الطبيعي طالما أن أحجام العينات كبيرة بما يكفي.

بالإضافة إلى ذلك، إذا كانت لديك عينات كبيرة للغاية، فإن الاختبارات الإحصائية مثل اختبار شابيرو ويلك ستخبرك دائمًا أن بياناتك ليست طبيعية. لهذا السبب، غالبًا ما يكون من الأفضل فحص بياناتك بصريًا باستخدام الرسوم البيانية مثل الرسوم البيانية ومخططات QQ. بمجرد النظر إلى الرسوم البيانية، يمكنك الحصول على فكرة جيدة عما إذا كانت البيانات يتم توزيعها بشكل طبيعي أم لا.

إذا تم انتهاك افتراض الحياة الطبيعية بشدة أو كنت تريد فقط أن تكون محافظًا للغاية، فلديك خياران:

(1) قم بتحويل قيم الاستجابة لبياناتك بحيث يتم توزيع التوزيعات بشكل طبيعي أكثر.

(2) إجراء اختبار غير معلمي مكافئ مثل اختبار كروسكال واليس الذي لا يتطلب افتراض الحالة الطبيعية.

الافتراض رقم 2: التباين المتساوي

تفترض ANOVA أن تباينات المجموعات السكانية التي تم سحب العينات منها متساوية.

كيفية التحقق من هذه الفرضية في R:

يمكننا التحقق من هذه الفرضية في R باستخدام طريقتين:

• بصريا التحقق من الفرضية باستخدام boxplots.
• اختبر الفرضية باستخدام الاختبارات الإحصائية الرسمية مثل اختبار بارتليت.

يوضح التعليمة البرمجية التالية كيفية القيام بذلك، باستخدام نفس مجموعة بيانات فقدان الوزن المزيفة التي أنشأناها سابقًا.

1. قم بإنشاء مخططات مربعة.

 #Create box plots that show distribution of weight loss for each group
boxplot(weight_loss ~ program, xlab=' Program ', ylab=' Weight Loss ', data=data)

يمكن ملاحظة التباين في فقدان الوزن في كل مجموعة من خلال طول كل قطعة مربعة. كلما زاد طول الصندوق، زاد التباين. على سبيل المثال، يمكننا أن نرى أن التباين أعلى قليلاً بالنسبة للمشاركين في البرنامج (ج) مقارنةً بالبرنامج (أ) والبرنامج (ب).

2. إجراء اختبار بارتليت.

 #Create box plots that show distribution of weight loss for each group
bartlett. test (weight_loss ~ program, data=data)

#Bartlett test of homogeneity of variances
#
#data: weight_loss by program
#Bartlett's K-squared = 8.2713, df = 2, p-value = 0.01599

يختبر اختبار بارتليت الفرضية الصفرية القائلة بأن العينات لها تباينات متساوية مقابل الفرضية البديلة القائلة بأن العينات ليس لها تباينات متساوية. في هذه الحالة، تكون القيمة p للاختبار هي 0.01599 ، وهي أقل من مستوى ألفا البالغ 0.05. وهذا يشير إلى أن العينات ليس لها نفس التباين.

ماذا تفعل إذا لم يتم احترام هذا الافتراض:

بشكل عام، يعتبر تحليل التباين أحادي الاتجاه قويًا إلى حد ما لانتهاكات افتراض التباينات المتساوية طالما أن كل مجموعة لها نفس حجم العينة.

ومع ذلك، إذا كانت أحجام العينات ليست هي نفسها وتم انتهاك هذا الافتراض بشدة، فيمكنك بدلاً من ذلك تشغيل اختبار Kruskal-Wallis ، وهو الإصدار غير المعلمي من ANOVA أحادي الاتجاه.

الافتراض رقم 3: الاستقلال

تفترض ANOVA:

• ملاحظات كل مجموعة مستقلة عن ملاحظات جميع المجموعات الأخرى.
• تم الحصول على الملاحظات داخل كل مجموعة عن طريق عينة عشوائية.

كيفية التحقق من هذه الفرضية:

لا يوجد اختبار رسمي يمكنك استخدامه للتحقق من أن الملاحظات في كل مجموعة مستقلة وأنه تم الحصول عليها عن طريق عينة عشوائية. الطريقة الوحيدة لتحقيق هذا الافتراض هي استخدام التصميم العشوائي.

ماذا تفعل إذا لم يتم احترام هذا الافتراض:

لسوء الحظ، ليس هناك الكثير الذي يمكنك فعله إذا لم يتم استيفاء هذا الافتراض. ببساطة، إذا تم جمع البيانات بطريقة تجعل الملاحظات في كل مجموعة غير مستقلة عن الملاحظات في المجموعات الأخرى، أو إذا لم يتم الحصول على الملاحظات داخل كل مجموعة من خلال عملية عشوائية، فلن تكون نتائج تحليل التباين (ANOVA) موثوقة .

إذا لم يتم استيفاء هذا الافتراض، فإن أفضل ما يمكنك فعله هو إعادة إنشاء التجربة باستخدام تصميم عشوائي.

قراءة متعمقة:

كيفية إجراء ANOVA أحادي الاتجاه في R
كيفية إجراء ANOVA أحادي الاتجاه في Excel