كيفية إجراء اختبار t للعينات المقترنة في excel

يتم استخدام اختبار t للعينات المقترنة لمقارنة متوسطي عينتين عندما يمكن ربط كل ملاحظة في عينة واحدة بملاحظة في العينة الأخرى.

يشرح هذا البرنامج التعليمي كيفية إجراء اختبار t للعينات المقترنة في Excel.

كيفية إجراء اختبار t للعينات المقترنة في Excel

لنفترض أننا نريد أن نعرف ما إذا كان منهج معين له تأثير كبير على أداء الطلاب في اختبار معين. ولاختبار ذلك، طلبنا من 20 طالبًا في الفصل إجراء اختبار مسبق. ثم نجعل كل طالب يشارك في المنهج لمدة أسبوعين. ثم يقوم الطلاب بإعادة إجراء اختبار بنفس الصعوبة.

لمقارنة الفرق بين متوسطي الدرجات في الاختبارين الأول والثاني، نستخدم اختبار t للعينات المزدوجة لأنه لكل طالب، يمكن ربط درجاته في الاختبار الأول بدرجاته في الاختبار الثاني.

الصورة التالية توضح درجة كل طالب في الاختبار القبلي ودرجة الاختبار البعدي:

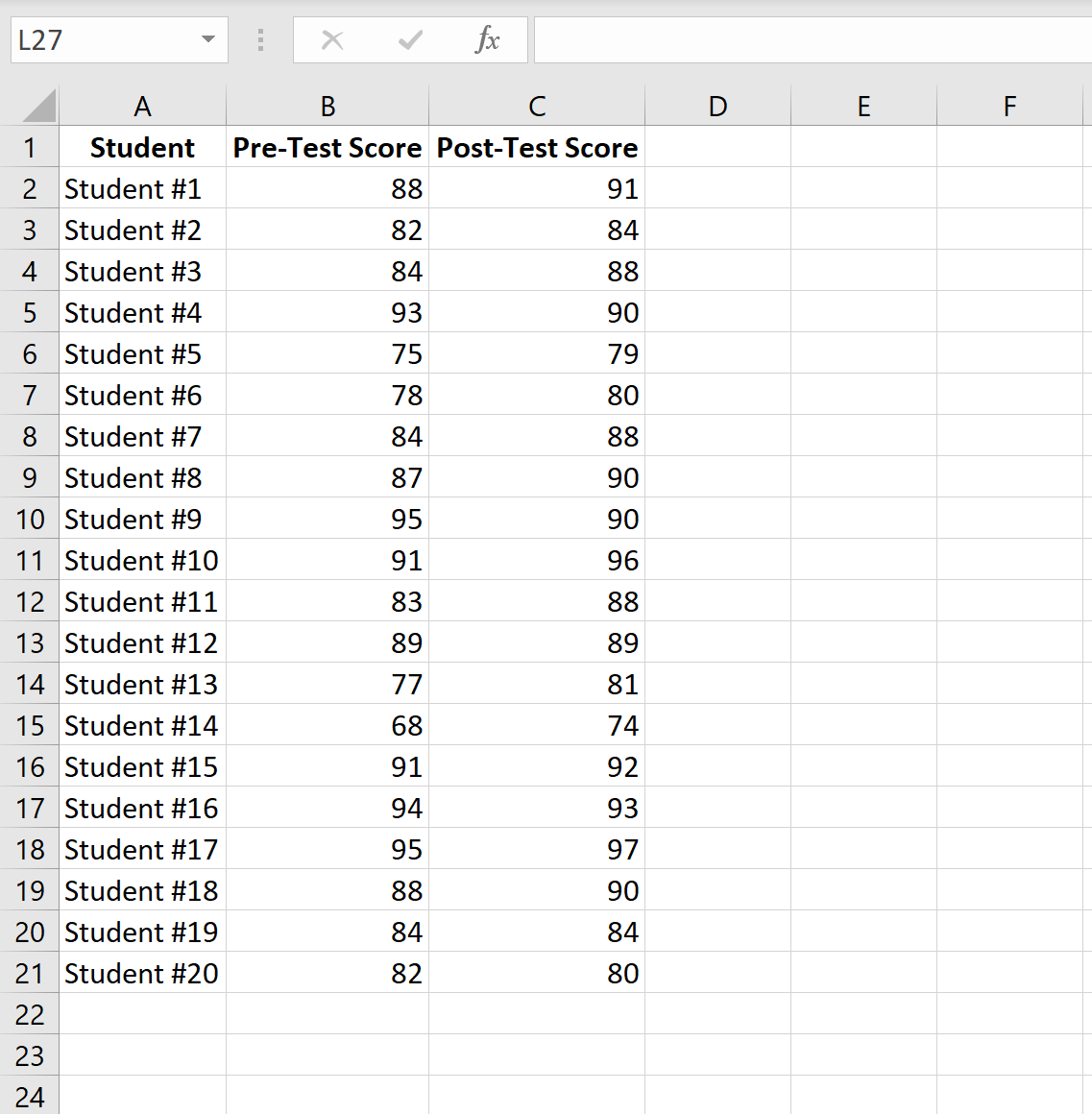
أكمل الخطوات التالية لإجراء اختبار t للعينات المقترنة لتحديد ما إذا كان هناك فرق كبير في متوسط درجات الاختبار بين الاختبار القبلي والاختبار البعدي.

الخطوة 1: افتح حزمة أدوات تحليل البيانات.

في علامة التبويب “البيانات” بالشريط العلوي، انقر فوق “تحليل البيانات”.

إذا لم تجد هذا الخيار للنقر عليه، فستحتاج أولاً إلى تنزيل Analysis ToolPak ، وهو مجاني تمامًا.

الخطوة 2: حدد الاختبار المناسب للاستخدام.

حدد الخيار الذي يقول T-Test: Paired Two Sample for Means ، ثم انقر فوق OK.

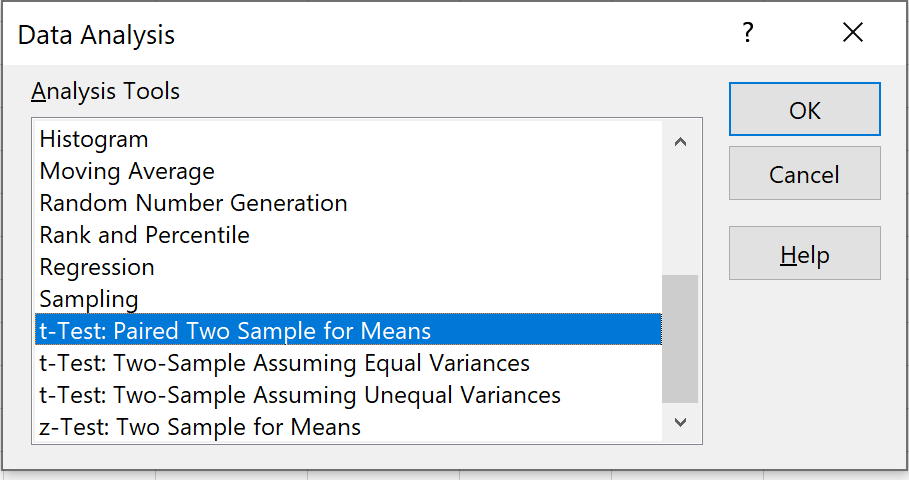
الخطوة 3: أدخل المعلومات اللازمة.

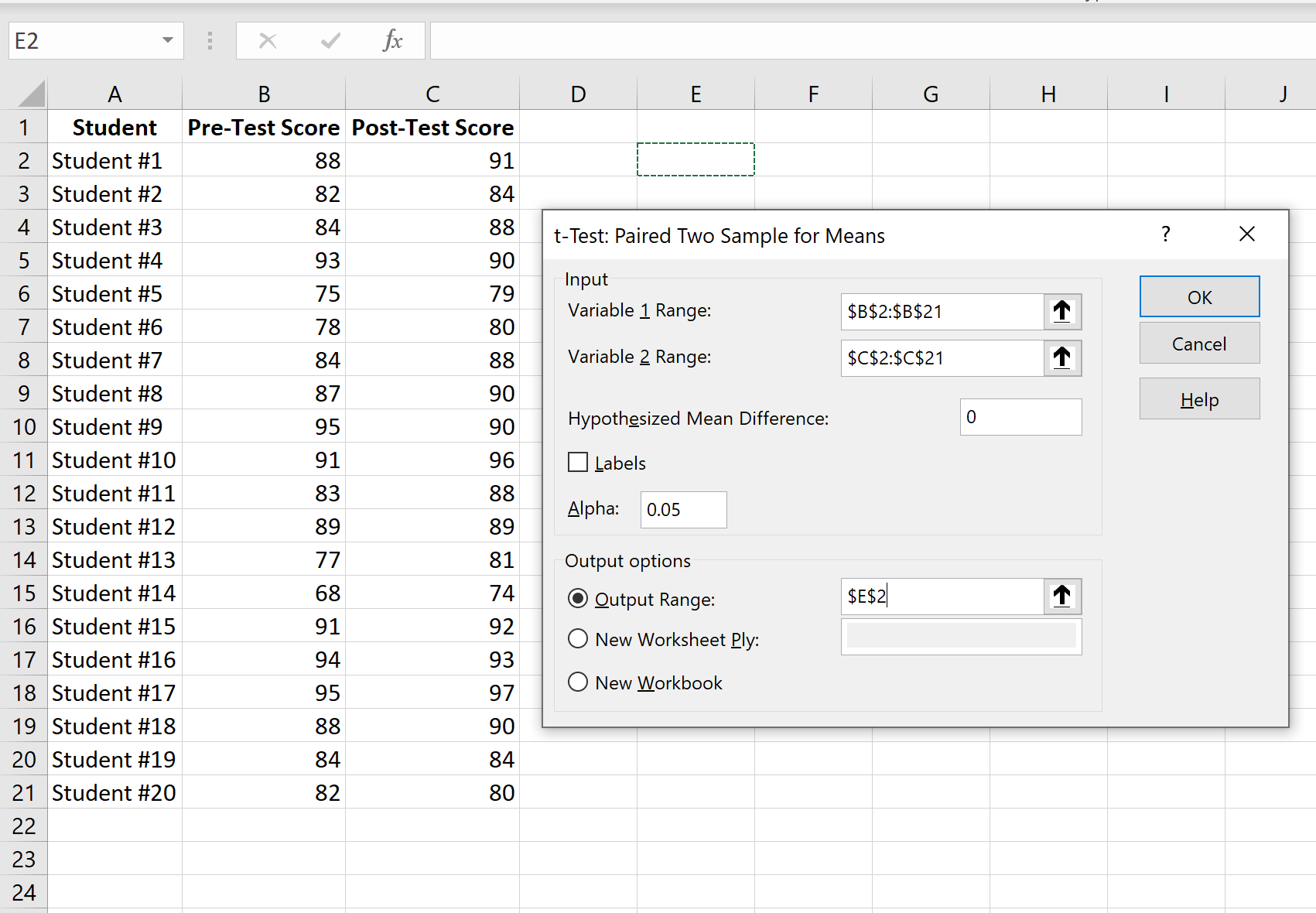
أدخل نطاق القيم للمتغير 1 (درجات الاختبار القبلي)، المتغير 2 (درجات الاختبار البعدي)، فرق المتوسط الافتراضي (في هذه الحالة نضع “0” لأننا نريد معرفة ما إذا كان الفرق الحقيقي المتوسط بين درجات ما قبل الاختبار وما بعده هو 0)، ونطاق الإخراج الذي نود أن نرى نتائج الاختبار معروضة فيه. ثم انقر فوق موافق.

الخطوة 4: تفسير النتائج.

بمجرد النقر فوق “موافق” في الخطوة السابقة، سيتم عرض نتائج اختبار t.

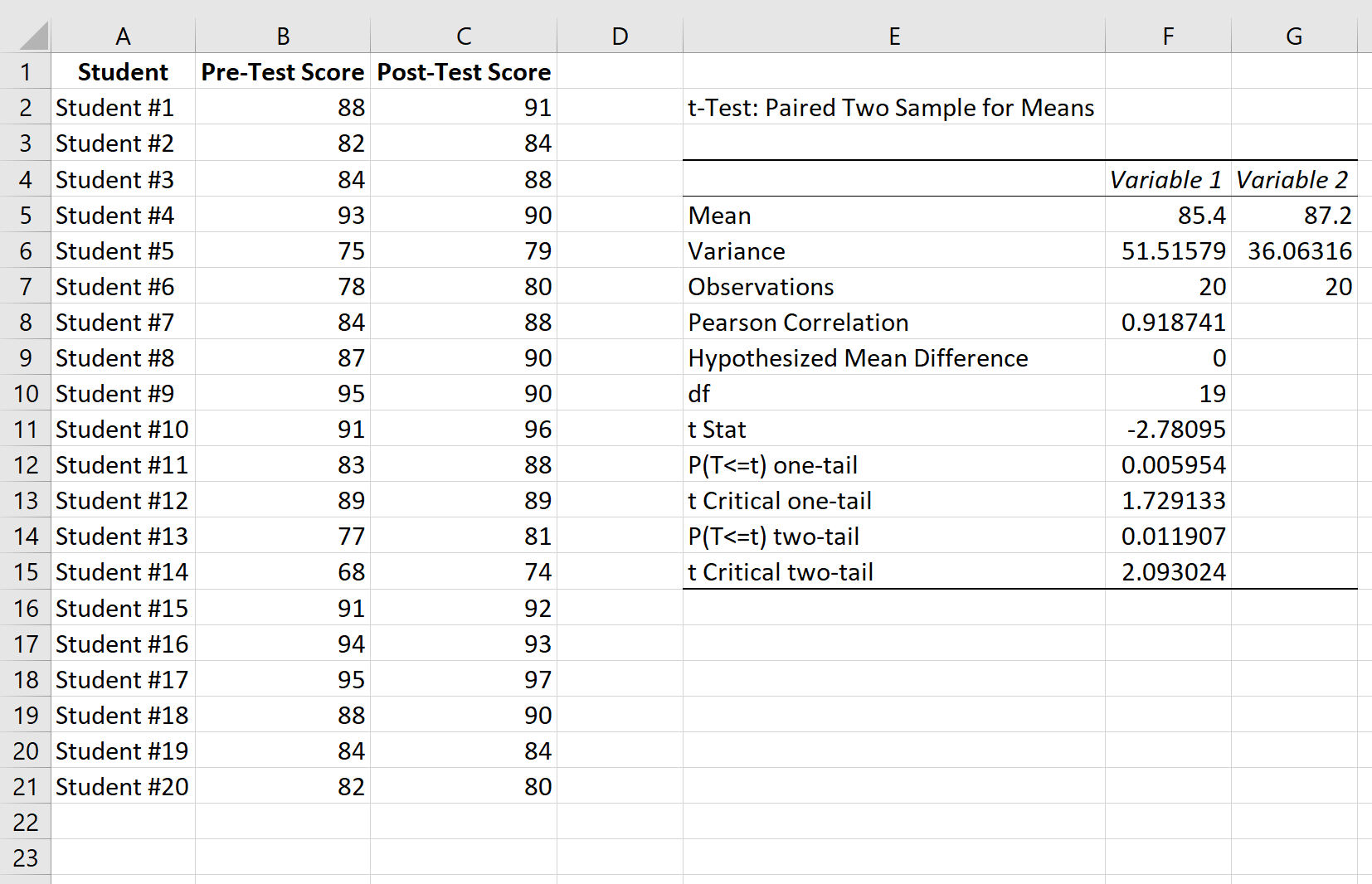
وإليك كيفية تفسير النتائج:

المتوسط: هذا هو متوسط كل عينة. متوسط درجات الاختبار القبلي هو 85.4 ومتوسط درجات الاختبار البعدي 87.2 .

التباين: هذا هو التباين لكل عينة. وكان التباين في درجات الاختبار القبلي 51.51 والتباين في درجات الاختبار البعدي 36.06 .

الملاحظات: هذا هو عدد الملاحظات في كل عينة. تحتوي كلا العينتين على 20 ملاحظة.

ارتباط بيرسون: العلاقة بين درجات الاختبار القبلي ودرجات الاختبار البعدي. وتبين أن 0.918 .

فرق المتوسط الافتراضي: الرقم الذي “نفترضه” هو الفرق بين المتوسطين. في هذه الحالة، اخترنا 0 لأننا نريد اختبار ما إذا كان هناك فرق بين درجات الاختبار القبلي والاختبار البعدي أم لا.

df: درجات الحرية للاختبار t. يتم حساب هذا كـ n-1 حيث n هو عدد الأزواج. في هذه الحالة، df = 20 – 1 = 19 .

t Stat: إحصائية اختبار t ، والتي تبين أنها -2.78 .

ثنائي الذيل P(T<=t): القيمة p لاختبار t ثنائي الذيل. في هذه الحالة، ع = 0.011907 . وهذا أصغر من alpha = 0.05، لذلك نرفض فرضية العدم. لدينا ما يكفي من الأدلة لنقول أن هناك فرق ذو دلالة إحصائية بين متوسط درجات الاختبار القبلي والبعدي.

t حرجة ثنائية الطرف: هذه هي القيمة الحرجة للاختبار، ويتم العثور عليها من خلال تحديد القيمة في جدول توزيع t الذي يتوافق مع اختبار ثنائي الطرف مع alpha = 0.05 وdf = 19. وتبين أن هذه هي 2، 093024 . وبما أن القيمة المطلقة لإحصائيات اختبار t أكبر من هذه القيمة، فإننا نرفض فرضية العدم. لدينا ما يكفي من الأدلة لنقول أن هناك فرق ذو دلالة إحصائية بين متوسط درجات الاختبار القبلي والبعدي.

لاحظ أن نهج القيمة p والقيمة الحرجة سيؤديان إلى نفس النتيجة.

مصادر إضافية

تشرح البرامج التعليمية التالية كيفية إجراء اختبارات t أخرى في Excel:

كيفية إجراء اختبار t لعينة واحدة في Excel
كيفية إجراء اختبار t من عينتين في برنامج Excel