كيفية إجراء anova أحادي الاتجاه في stata

يتم استخدام ANOVA أحادي الاتجاه لتحديد ما إذا كان هناك فرق ذو دلالة إحصائية بين متوسطات ثلاث مجموعات مستقلة أو أكثر أم لا.

يُطلق على هذا النوع من الاختبارات اسم ANOVA أحادي الاتجاه لأننا نقوم بتحليل تأثير متغير التوقع على متغير الاستجابة. إذا كنا مهتمين بدلاً من ذلك بتأثير متغيرين متوقعين على متغير الاستجابة، فيمكننا إجراء تحليل التباين (ANOVA) ثنائي الاتجاه .

يشرح هذا البرنامج التعليمي كيفية إجراء ANOVA أحادي الاتجاه في Stata.

مثال: ANOVA أحادي الاتجاه في Stata

في هذا المثال، سوف نستخدم مجموعة بيانات Stata المضمنة والتي تسمى الانقباضي لإجراء تحليل التباين أحادي الاتجاه. تحتوي مجموعة البيانات هذه على المتغيرات الثلاثة التالية لـ 58 فردًا مختلفًا:

• المخدرات المستخدمة
• مرض المريض
• تغير في ضغط الدم الانقباضي

سوف نستخدم الخطوات التالية لإجراء تحليل التباين (ANOVA) أحادي الاتجاه لتحديد ما إذا كان نوع الدواء المستخدم يؤدي إلى تأثير كبير على التغير في ضغط الدم الانقباضي.

الخطوة 1: تحميل البيانات.

أولاً، قم بتحميل البيانات عن طريق كتابة webuse systolic في مربع الأوامر والنقر فوق Enter.

الخطوة 2: عرض البيانات الأولية.

قبل إجراء تحليل التباين أحادي الاتجاه، دعونا نلقي نظرة أولاً على البيانات الأولية. من شريط القائمة العلوي، انتقل إلى Data > Data Editor > Data Editor (Browse) . سيُظهر لنا هذا البيانات الفعلية لجميع المرضى البالغ عددهم 58 مريضًا:

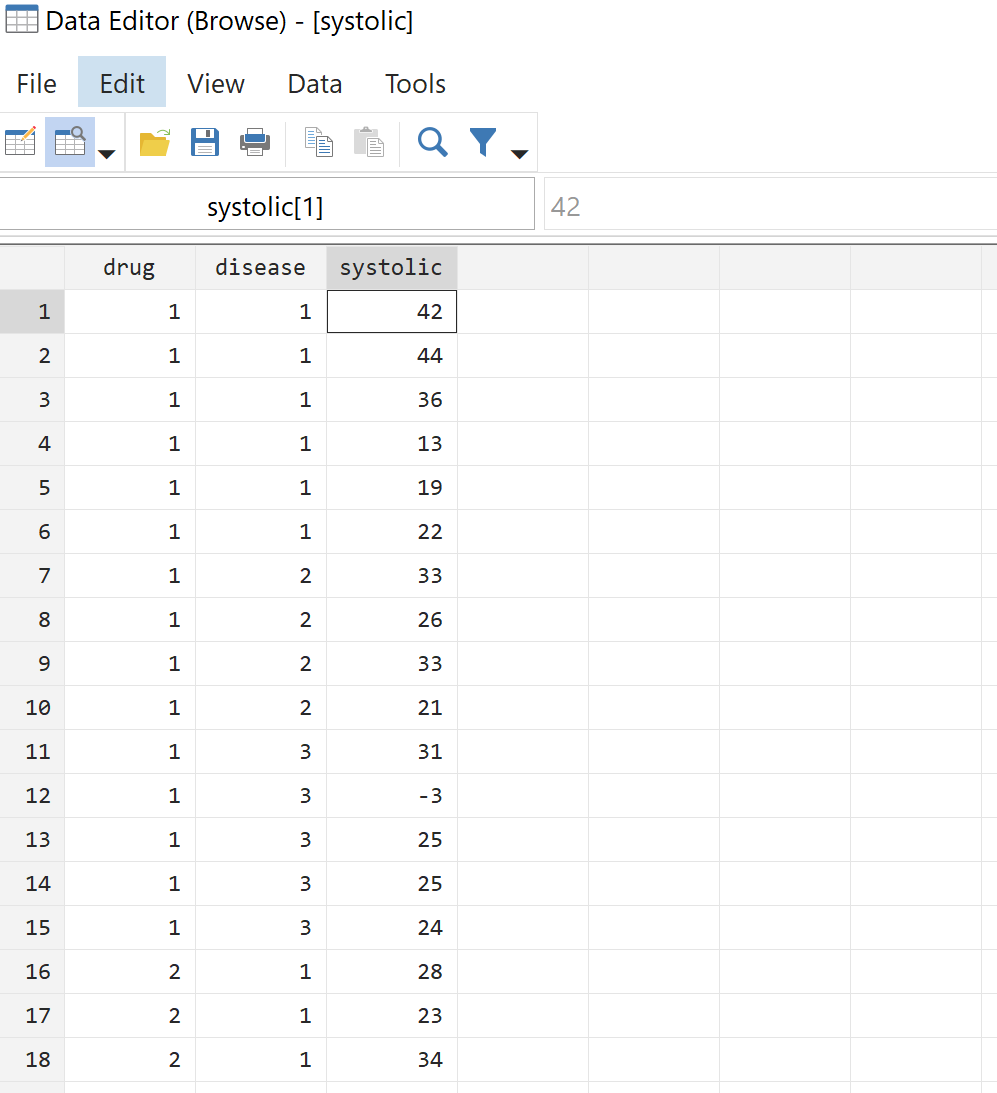
الخطوة 3: تصور البيانات.

بعد ذلك، دعونا تصور البيانات. سنقوم بإنشاء مخططات مربعة لعرض توزيع قيم ضغط الدم الانقباضي لكل فئة من فئات الأدوية.

من شريط القائمة العلوي، انتقل إلى المخططات > رسم المربع . ضمن المتغيرات، اختر الانقباضي:

ثم، في العنوان الفرعي الفئات ضمن متغير التجميع، اختر الدواء:

انقر فوق موافق . سيتم عرض مخطط يحتوي على أربعة مخططات boxplots تلقائيًا:

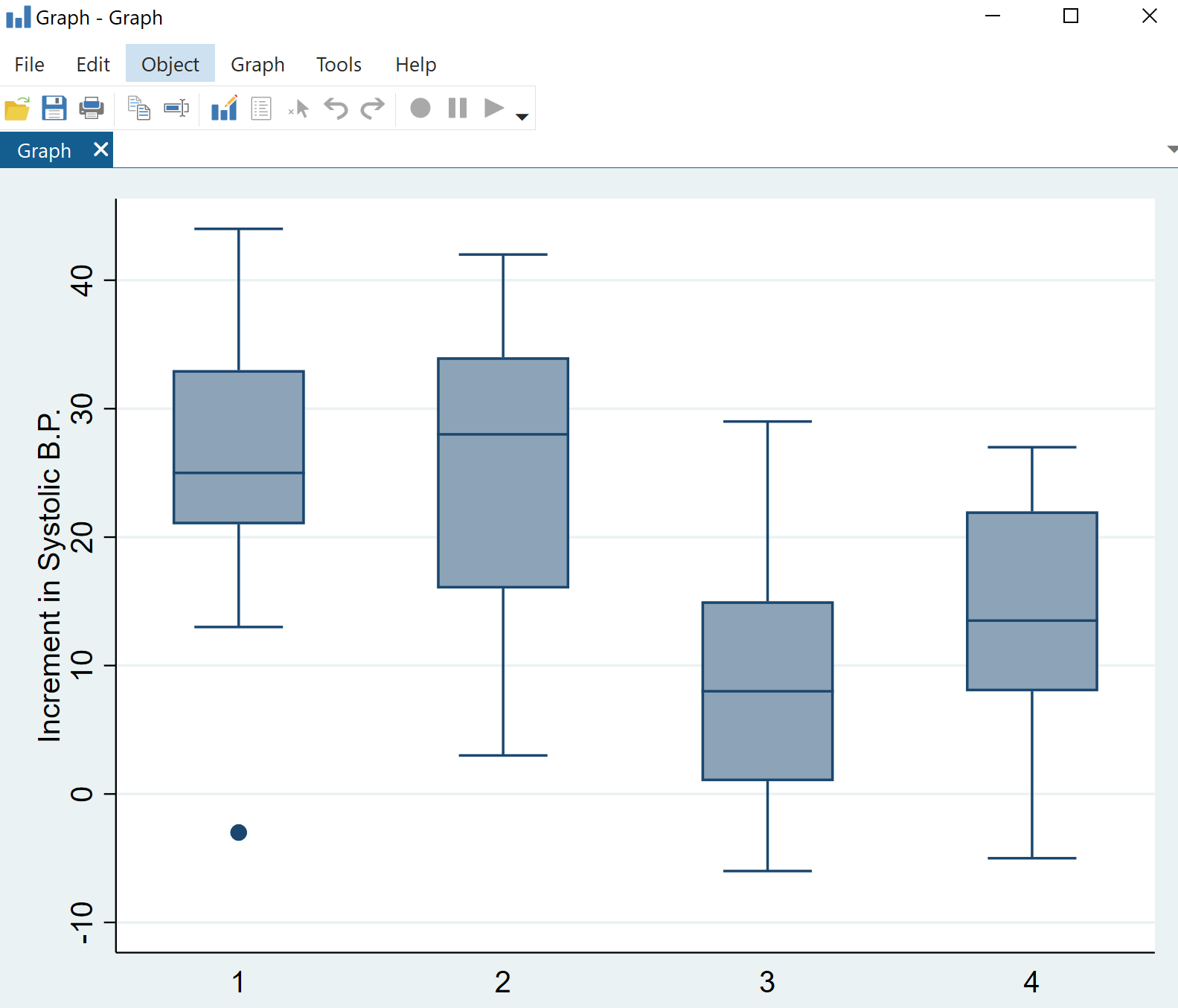
يمكننا أن نرى على الفور أن توزيع التغيرات في ضغط الدم الانقباضي يختلف عبر فئات الأدوية، ولكن تحليل التباين أحادي الاتجاه سيخبرنا ما إذا كانت هذه الاختلافات ذات دلالة إحصائية.

الخطوة 4: إجراء تحليل التباين (ANOVA) في اتجاه واحد.

من شريط القائمة العلوي، انتقل إلى الإحصائيات > النماذج الخطية والنماذج ذات الصلة > ANOVA/MANOVA > One-Way ANOVA .

ضمن متغير الاستجابة، اختر الانقباضي. ضمن متغير العامل، اختر الدواء. ثم انقر فوق المربع الموجود بجوار إنتاج جدول ملخص حتى نتمكن من رؤية بعض الإحصائيات الوصفية الأساسية لكل مجموعة. ثم انقر فوق موافق .

سيتم عرض الإخراج التالي:

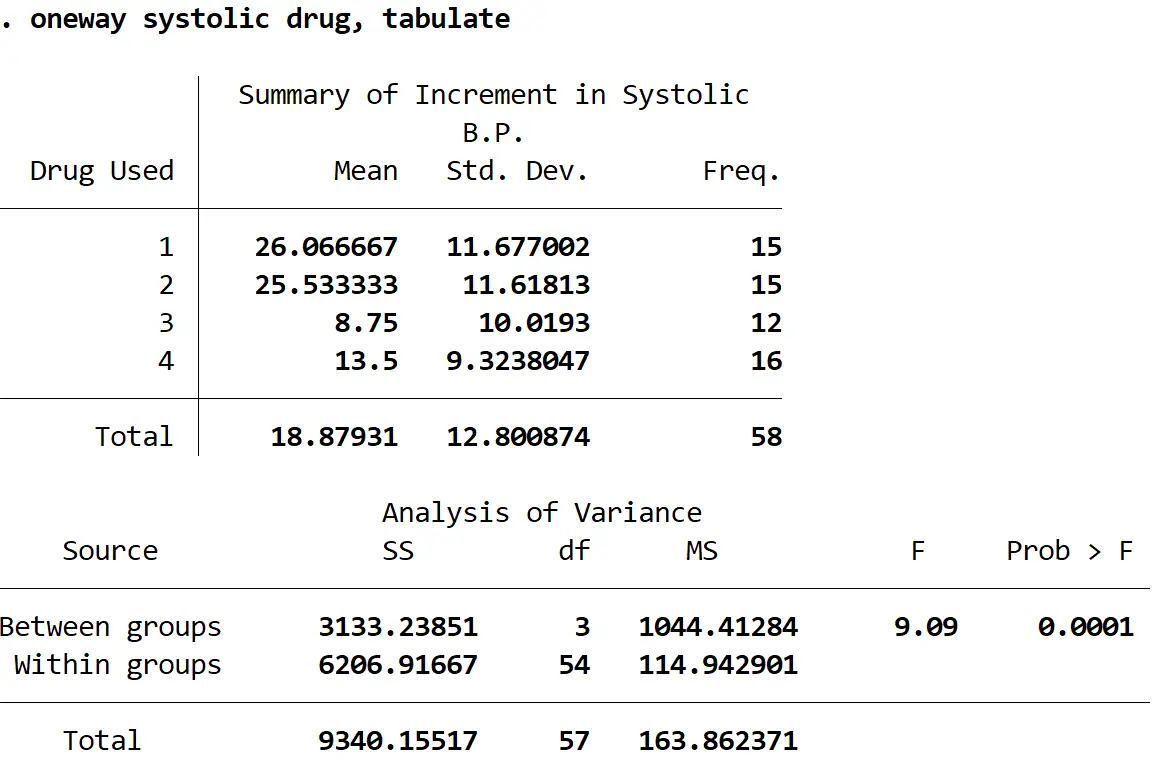
إحصائيات F هي 9.09 والقيمة p المقابلة هي 0.0001 . وبما أن القيمة p أقل من alpha = 0.05، فيمكننا رفض فرضية العدم القائلة بأن متوسط التغير في ضغط الدم الانقباضي لكل مجموعة متساوٍ.

بمعنى آخر، هناك فرق ذو دلالة إحصائية في متوسط التغير في ضغط الدم الانقباضي بين مجموعتين دوائيتين على الأقل.

الخطوة 5: إجراء اختبارات مقارنة متعددة.

ثم يمكننا إجراء العديد من اختبارات المقارنة لمعرفة متوسطات المجموعة التي تختلف عن بعضها البعض.

من شريط القائمة العلوي، انتقل إلى الإحصائيات > الملخصات والجداول والاختبارات > الملخص والإحصائيات الوصفية > المقارنات الزوجية للوسائل .

بالنسبة للمتغير، اختر متغير الاستجابة الانقباضية . بالنسبة لـ Over اختر المتغير التوضيحي للدواء . لضبط المقارنات المتعددة، اختر طريقة Tukey .

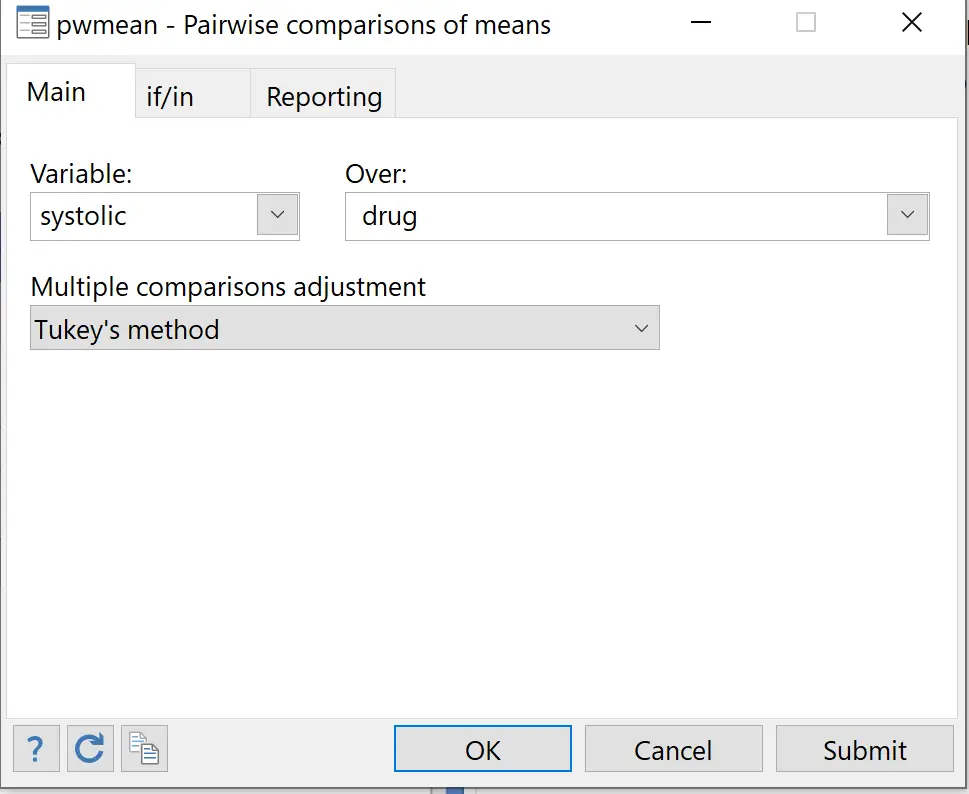
بعد ذلك، ضمن العنوان الفرعي إعداد التقارير ، انقر فوق الزر الموجود بجوار جداول التأثيرات وحدد المربع بجوار عرض جدول التأثيرات بفواصل الثقة والقيم الاحتمالية . ثم انقر فوق موافق .

سيتم عرض النتائج التالية:

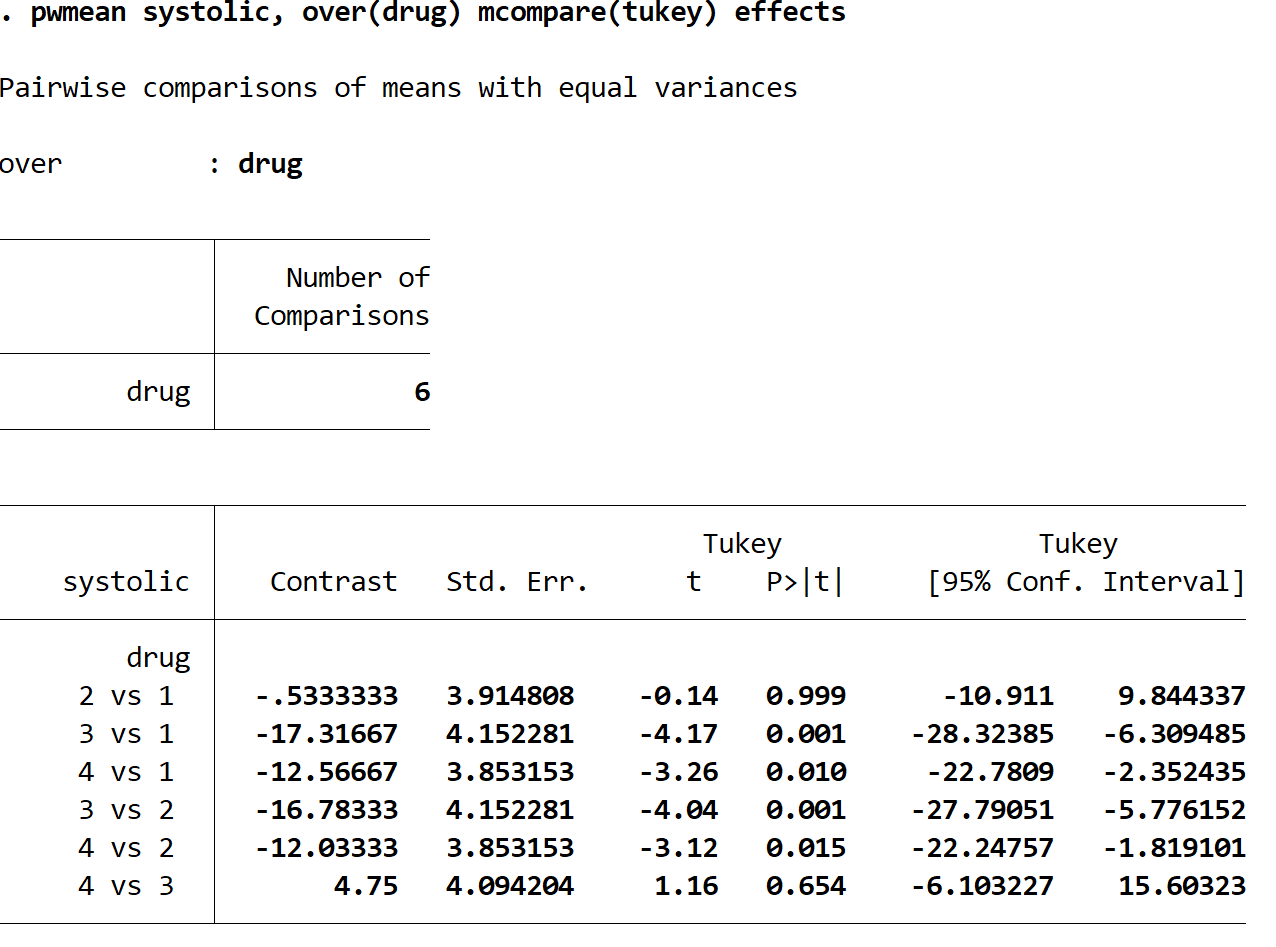
يمثل كل صف مقارنة بين مجموعتين محددتين من الأدوية. على سبيل المثال، يقارن الصف الأول متوسط التغير في ضغط الدم الانقباضي بين مجموعة الأدوية 2 ومجموعة الأدوية 1. القيمة p لهذه المقارنة هي 0.999 ، وهي عالية للغاية ولا تقل عن 0.05. وهذا يعني أنه لا يوجد فرق ذو دلالة إحصائية بين مجموعتي الأدوية 1 و 2.

ومع ذلك، يمكننا أن نرى أن القيم الاحتمالية للمقارنات التالية جميعها أقل من 0.05:

• الطب 3 إلى 1 | القيمة p = 0.001
• الطب 4 إلى 1 | القيمة p = 0.010
• الطب 3 ضد 2 | القيمة p = 0.001
• الطب 4 ضد 2 | القيمة p = 0.015

وهذا يعني أن الفرق في متوسط التغير في ضغط الدم الانقباضي له دلالة إحصائية بين كل من هذه المجموعات.

الخطوة 6: الإبلاغ عن النتائج.

وأخيرا، سوف نقوم بالإبلاغ عن نتائج تحليل ANOVA أحادي الاتجاه. فيما يلي مثال لكيفية القيام بذلك:

تم إجراء ANOVA أحادي الاتجاه لتحديد ما إذا كانت أربعة أنواع مختلفة من الأدوية لها تأثيرات مختلفة على ضغط الدم الانقباضي.

يلخص الجدول التالي عدد المشاركين في كل مجموعة وكذلك متوسط التغير في ضغط الدم الانقباضي والانحراف المعياري لضغط الدم الانقباضي لكل مجموعة:

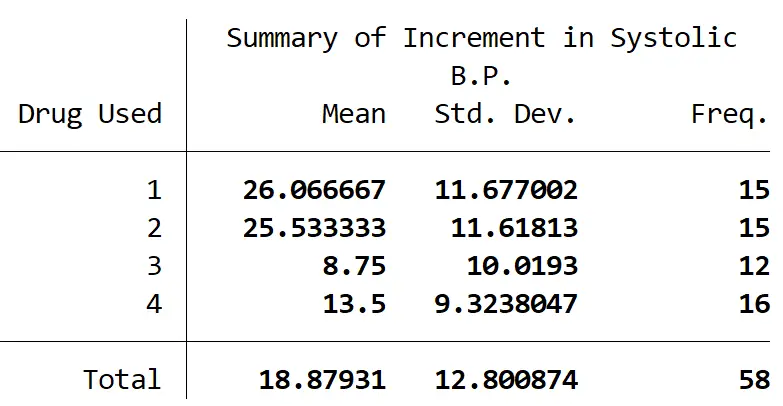
كشفت ANOVA أحادية الاتجاه أن هناك فرقًا ذا دلالة إحصائية بين مجموعتين على الأقل (F(3, 54) = 9.09، p = 0.001).

كشف اختبار توكي لإجراء مقارنات متعددة أن التغير في ضغط الدم الانقباضي كان أعلى بشكل ملحوظ إحصائيًا بالنسبة للعقار 3 مقارنة بالعقار 1 (17.32 +/- 4.15، p = 0.001)، للعقار 3 مقارنة بالعقار 2 (16.78 +/- 4.15، ع = 0.001)، للمخدرات 4 مقارنة بالمخدرات 1 (12.57 +/- 3.85، ع = 0.010)، وللمخدرات 4 مقارنة بالمخدرات 2 (12.03 +/- 3.85، ع = 0.015).

لم يكن هناك فروق ذات دلالة إحصائية بين مجموعات المخدرات 1 و 2 (0.533 +/- 3.91، ع = 0.999) أو بين مجموعات المخدرات 3 و 4 (4.75 +/- 4.09، ع = 0.654).