كيفية إجراء اختبار breusch-pagan في برنامج excel

يتم استخدام اختبار Breusch-Pagan لتحديد ما إذا كانت التغايرية موجودة في تحليل الانحدار.

يشرح هذا البرنامج التعليمي كيفية إجراء اختبار Breusch-Pagan في برنامج Excel.

مثال: اختبار Breusch-Pagan في Excel

في هذا المثال، سوف نستخدم مجموعة البيانات التالية التي تصف سمات 10 من لاعبي كرة السلة.

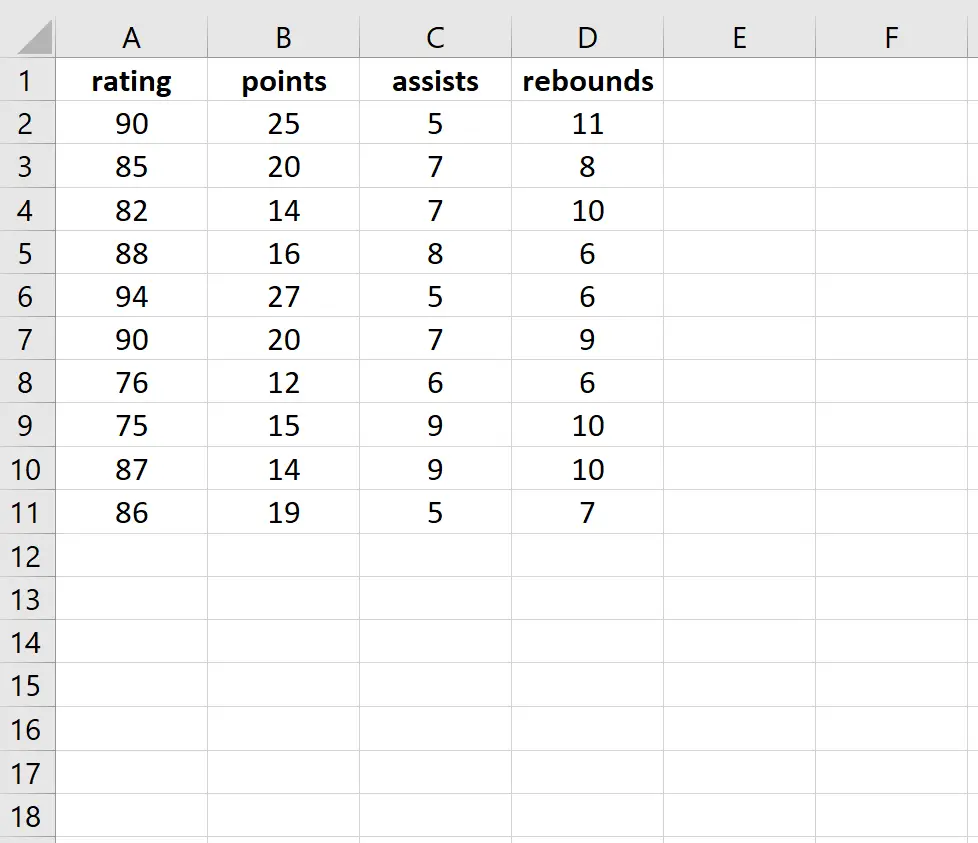
سوف نقوم بتركيب نموذج الانحدار الخطي المتعدد باستخدام التسجيل كمتغير الاستجابة والنقاط والتمريرات والمرتدات كمتغيرات توضيحية. بعد ذلك، سنقوم بإجراء اختبار Breusch-Pagan لتحديد ما إذا كانت التغايرية موجودة في الانحدار.

الخطوة 1: تنفيذ الانحدار الخطي المتعدد.

في الشريط العلوي لبرنامج Excel، انتقل إلى علامة التبويب “بيانات” وانقر فوق “تحليل البيانات”. إذا لم تشاهد هذا الخيار، فيجب عليك أولاً تثبيت برنامج Analysis ToolPak المجاني .

بمجرد النقر على تحليل البيانات، ستظهر نافذة جديدة. حدد الانحدار وانقر فوق موافق. أكمل الجداول اللازمة لمتغيرات الاستجابة والمتغيرات التوضيحية، ثم انقر فوق موافق.

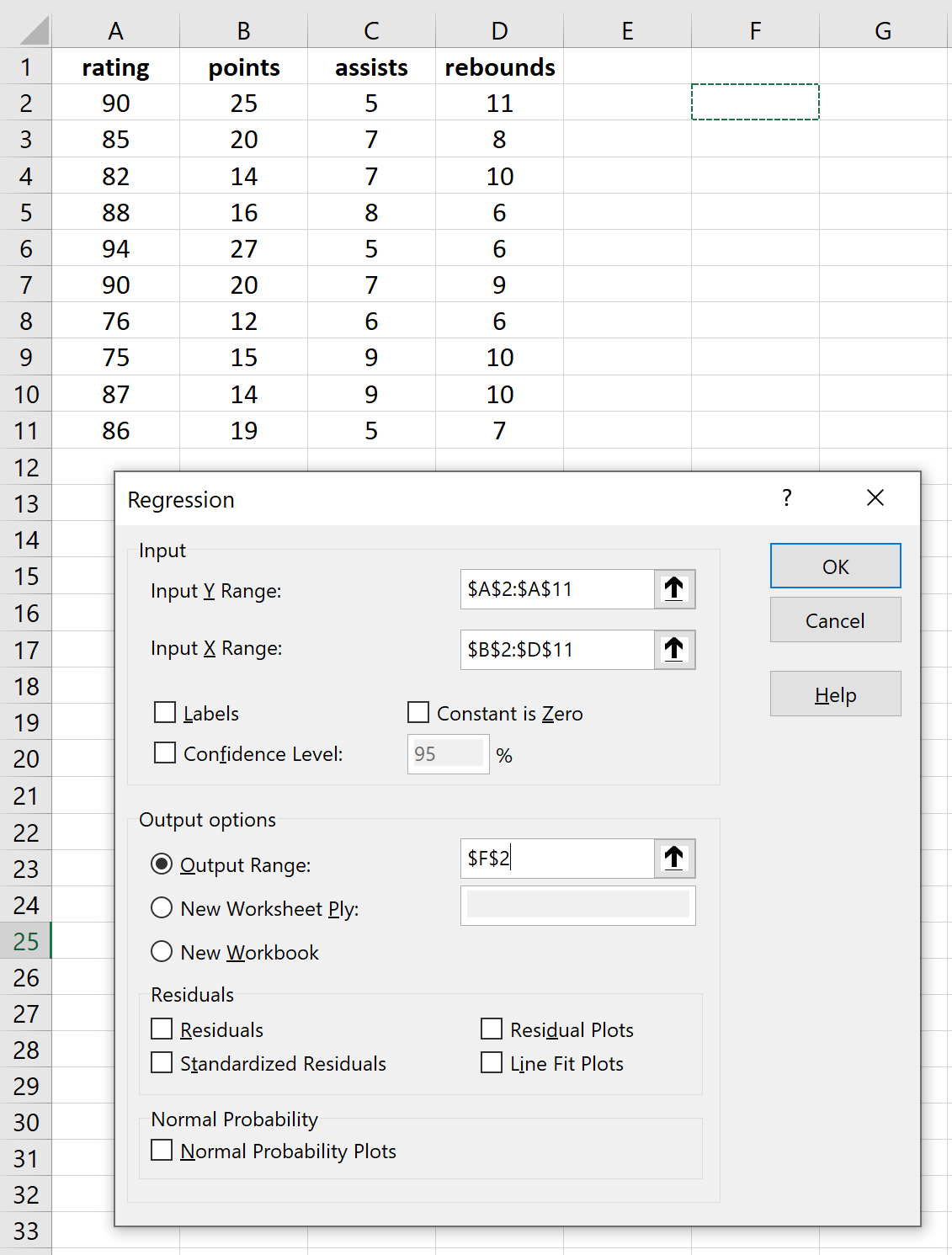
وهذا ينتج النتيجة التالية:

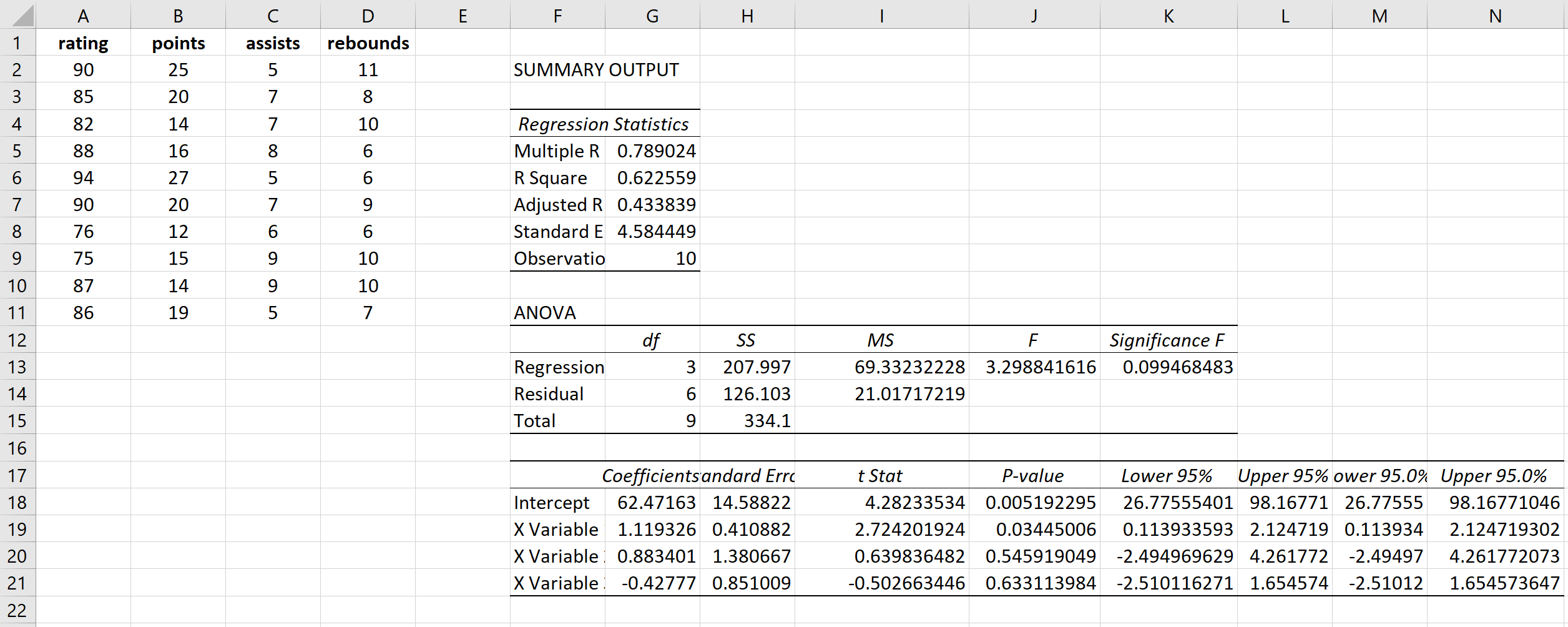
الخطوة 2: حساب مربعات البقايا.

بعد ذلك، سوف نقوم بحساب القيم المتوقعة والمتبقيات المربعة لكل قيمة استجابة. لحساب القيم المتوقعة، سوف نستخدم المعاملات من نتيجة الانحدار:

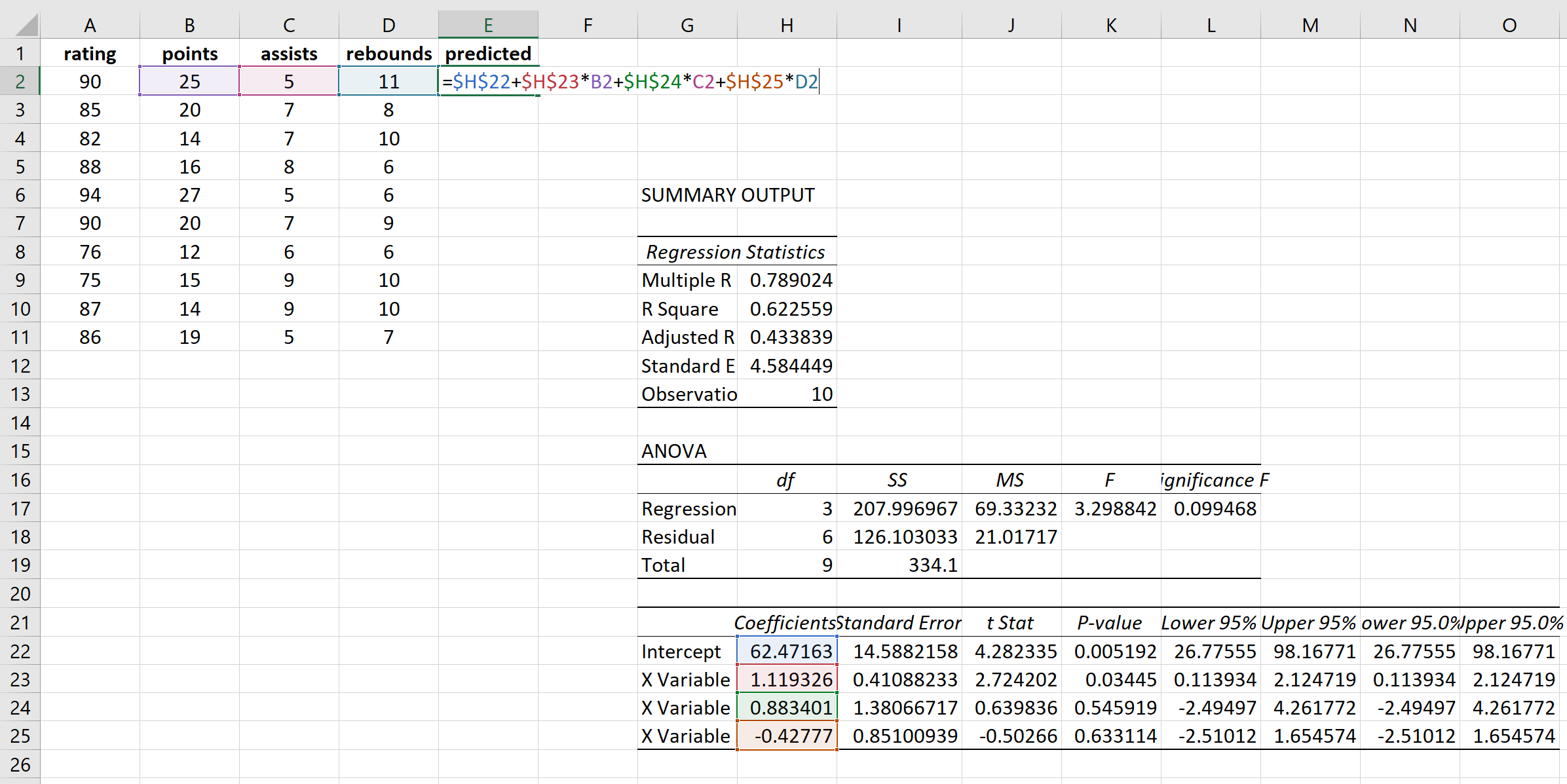
سوف نستخدم نفس الصيغة للحصول على كل قيمة متوقعة:

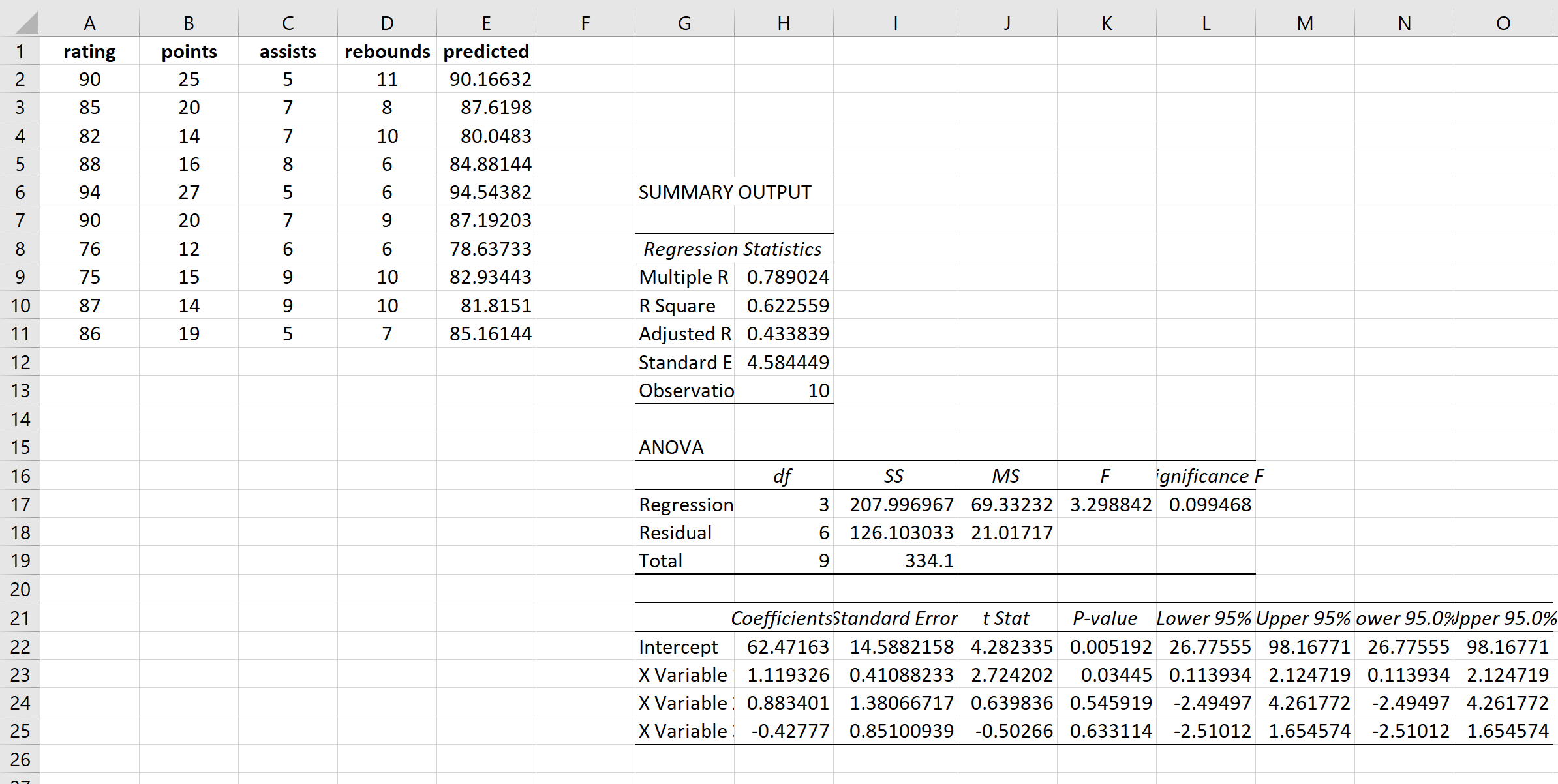
بعد ذلك، سوف نقوم بحساب مربعات البقايا لكل توقع:

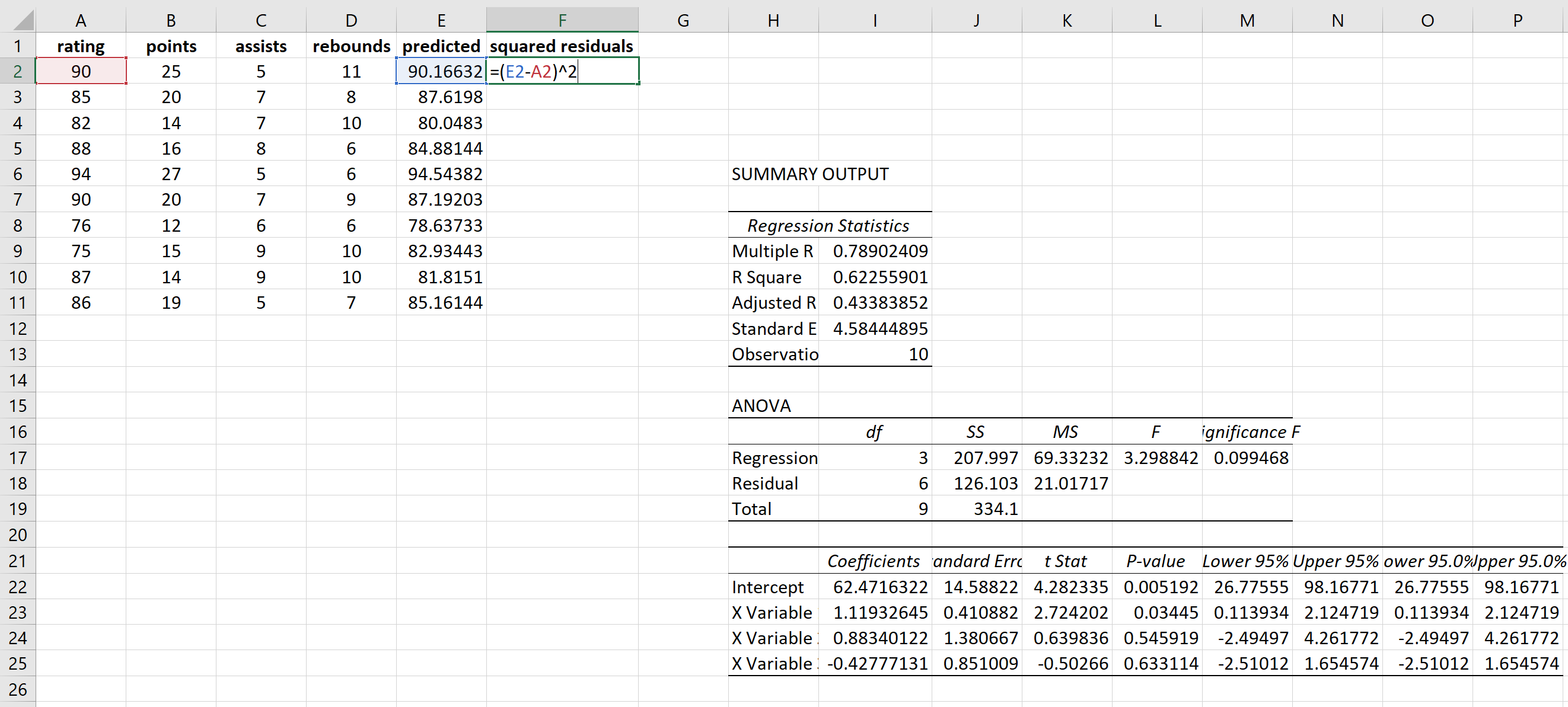
سوف نستخدم نفس الصيغة للحصول على كل مربع متبقي:

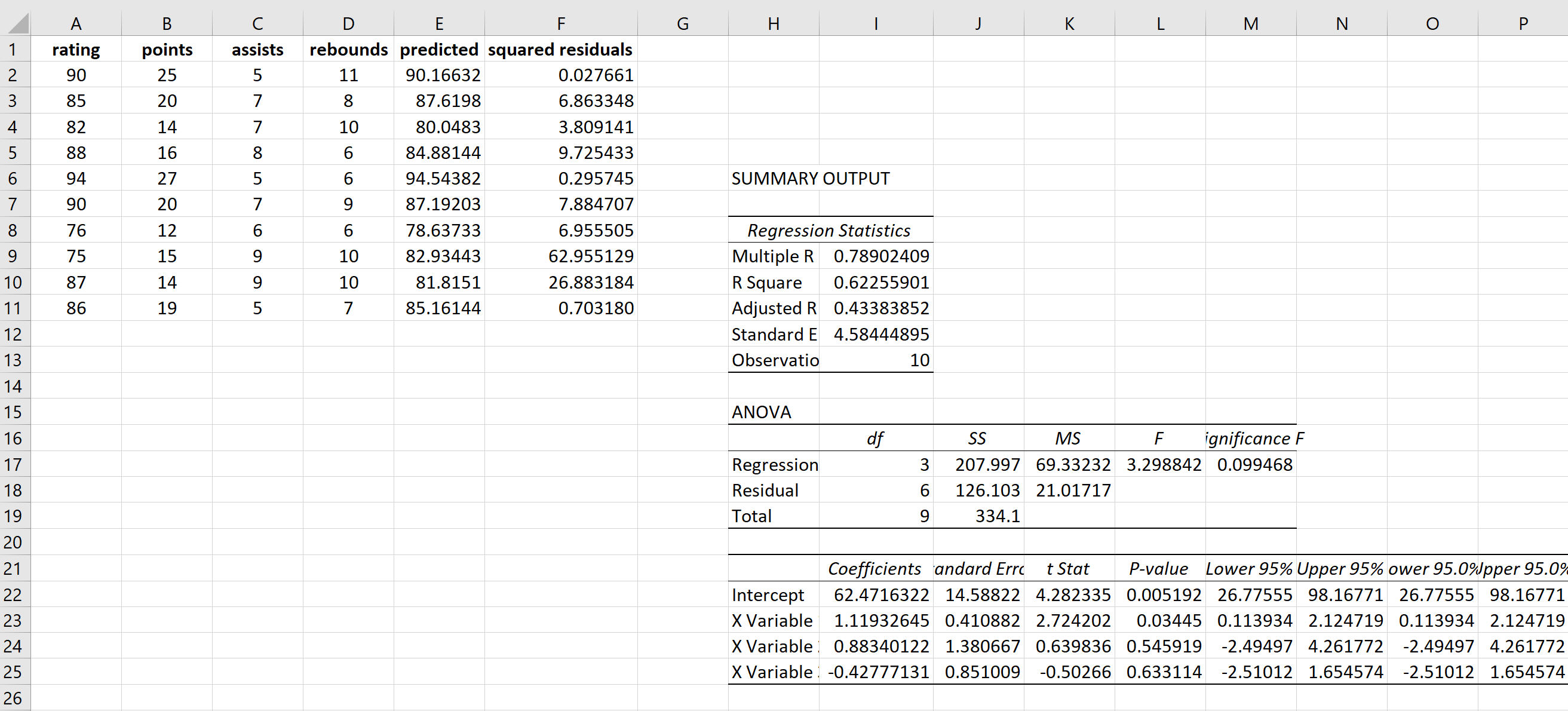
الخطوة 3: قم بإجراء انحدار خطي متعدد جديد باستخدام مربعات القيم المتبقية كقيم الاستجابة.

بعد ذلك، سنقوم بتنفيذ نفس الخطوات السابقة لإجراء انحدار خطي متعدد باستخدام النقاط والتمريرات والارتدادات كمتغيرات توضيحية، باستثناء هذه المرة سنستخدم مربعات البقايا كقيم الاستجابة. وهذه هي نتيجة هذا الانحدار:

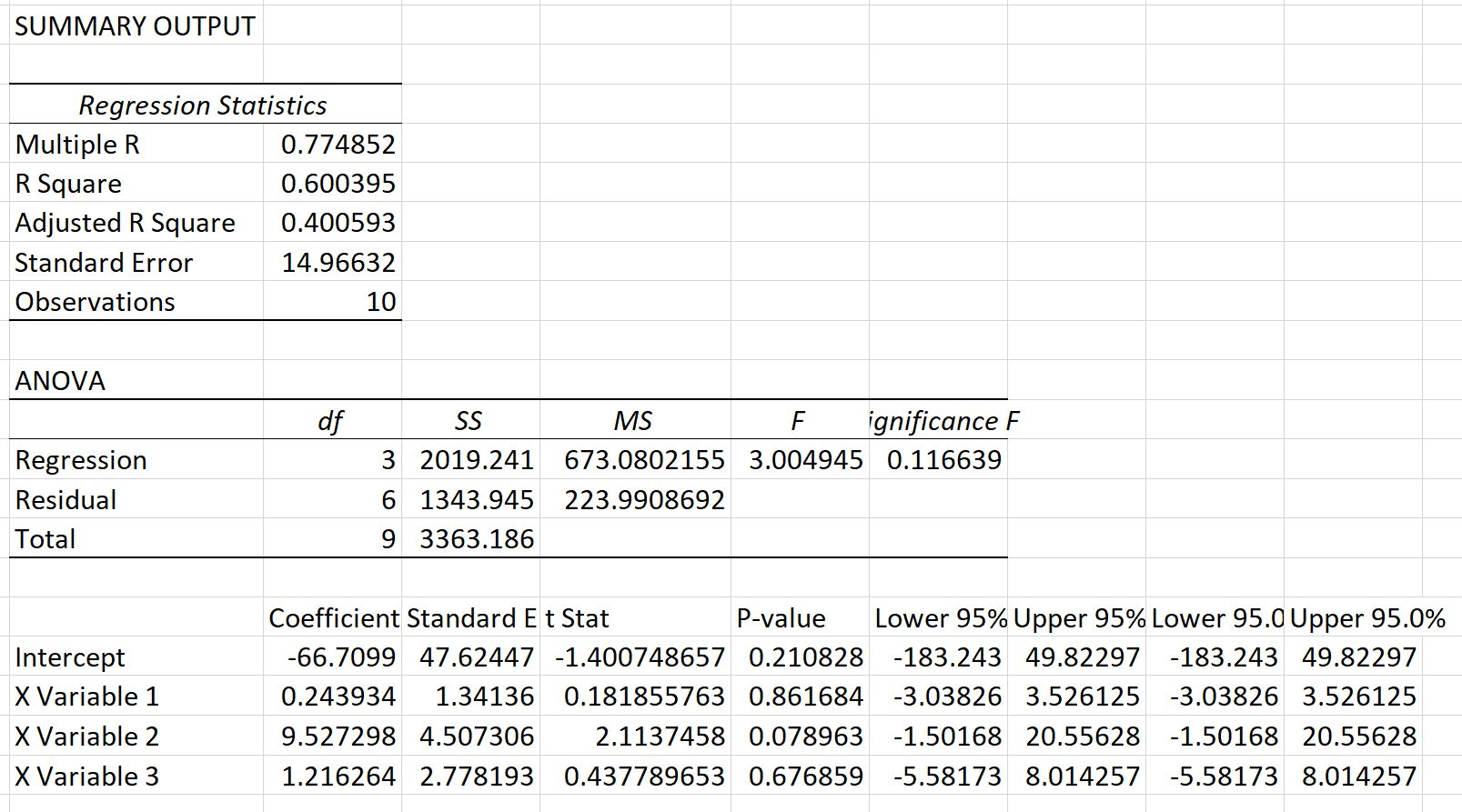
الخطوة 4: إجراء اختبار Breusch-Pagan.

أخيرًا، سنقوم بإجراء اختبار Breusch-Pagan لمعرفة ما إذا كانت التغايرية موجودة في الانحدار الأصلي.

سنقوم أولاً بحساب إحصائية اختبار مربع كاي باستخدام الصيغة:

X ² = ن*ر ² _جديد

ذهب:

ن = عدد الملاحظات

R ² _new = R مربع الانحدار “الجديد” الذي استخدمت فيه مربعات البقايا كمتغير الاستجابة.

في مثالنا X ² = 10 * 0.600395 = 6.00395 .

بعد ذلك، سوف نجد القيمة p المرتبطة بإحصائيات الاختبار هذه. يمكننا استخدام الصيغة التالية في Excel للقيام بذلك:

=CHISQ.DIST.RT(إحصائية الاختبار، درجات الحرية)

في حالتنا، درجات الحرية هي الرقم المحدد للانحدار df في الإخراج. في هذه الحالة، هو 3. لذا تصبح صيغتنا:

=CHISQ.DIST.RT(6.00395, 3) = 0.111418 .

وبما أن هذه القيمة p لا تقل عن 0.05، فإننا نفشل في رفض فرضية العدم. ليس لدينا ما يكفي من الأدلة للادعاء بأن التغايرية موجودة في نموذج الانحدار الأصلي.