كيفية إجراء الانحدار الهرمي في ستاتا

الانحدار الهرمي هو أسلوب يمكننا استخدامه لمقارنة عدة نماذج خطية مختلفة.

الفكرة الأساسية هي أننا أولاً نلائم نموذج الانحدار الخطي بمتغير توضيحي واحد. بعد ذلك، نقوم بتركيب نموذج انحدار آخر باستخدام متغير توضيحي إضافي. إذا كانت نسبة R-squared (نسبة التباين في متغير الاستجابة التي يمكن تفسيرها بالمتغيرات التوضيحية) في النموذج الثاني أعلى بكثير من R-squared في النموذج السابق، فهذا يعني أن النموذج الثاني أفضل.

ثم نكرر عملية تركيب نماذج الانحدار الإضافية بمتغيرات توضيحية أكثر ونرى ما إذا كانت النماذج الأحدث تقدم تحسينًا عن النماذج السابقة.

يقدم هذا البرنامج التعليمي مثالاً لكيفية إجراء الانحدار الهرمي في Stata.

مثال: الانحدار الهرمي في ستاتا

سوف نستخدم مجموعة بيانات مدمجة تسمى auto لتوضيح كيفية إجراء الانحدار الهرمي في Stata. أولاً، قم بتحميل مجموعة البيانات عن طريق كتابة ما يلي في مربع الأمر:

الاستخدام التلقائي للنظام

يمكننا الحصول على ملخص سريع للبيانات باستخدام الأمر التالي:

كي تختصر

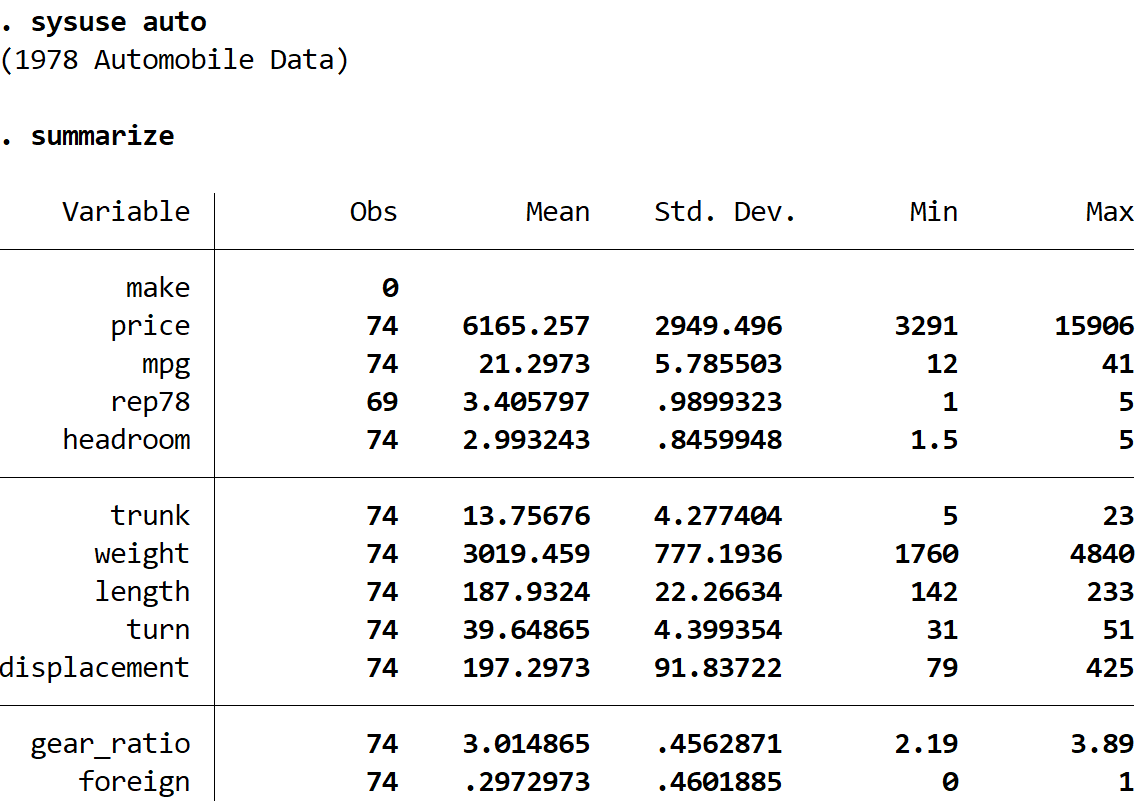
يمكننا أن نرى أن مجموعة البيانات تحتوي على معلومات حول 12 متغيرًا مختلفًا لـ 74 سيارة إجمالاً.

سوف نلائم نماذج الانحدار الخطي الثلاثة التالية ونستخدم الانحدار الهرمي لمعرفة ما إذا كان كل نموذج لاحق يوفر تحسنًا كبيرًا مقارنة بالنموذج السابق أم لا:

النموذج 1: السعر = الاعتراض + ميل لكل جالون

النموذج 2: السعر = التقاطع + ميل لكل جالون + الوزن

النموذج 3: السعر = التقاطع + ميل لكل جالون + الوزن + نسبة التروس

من أجل إجراء الانحدار الهرمي في Stata، سنحتاج أولاً إلى تثبيت حزمة Hireg . للقيام بذلك، اكتب ما يلي في مربع الأوامر:

ابحث عن هيريج

في النافذة التي تظهر، انقر فوق Hireg من https://fmwww.bc.edu/RePEc/bocode/h

في النافذة التالية، انقر فوق الرابط الذي يقول انقر هنا للتثبيت .

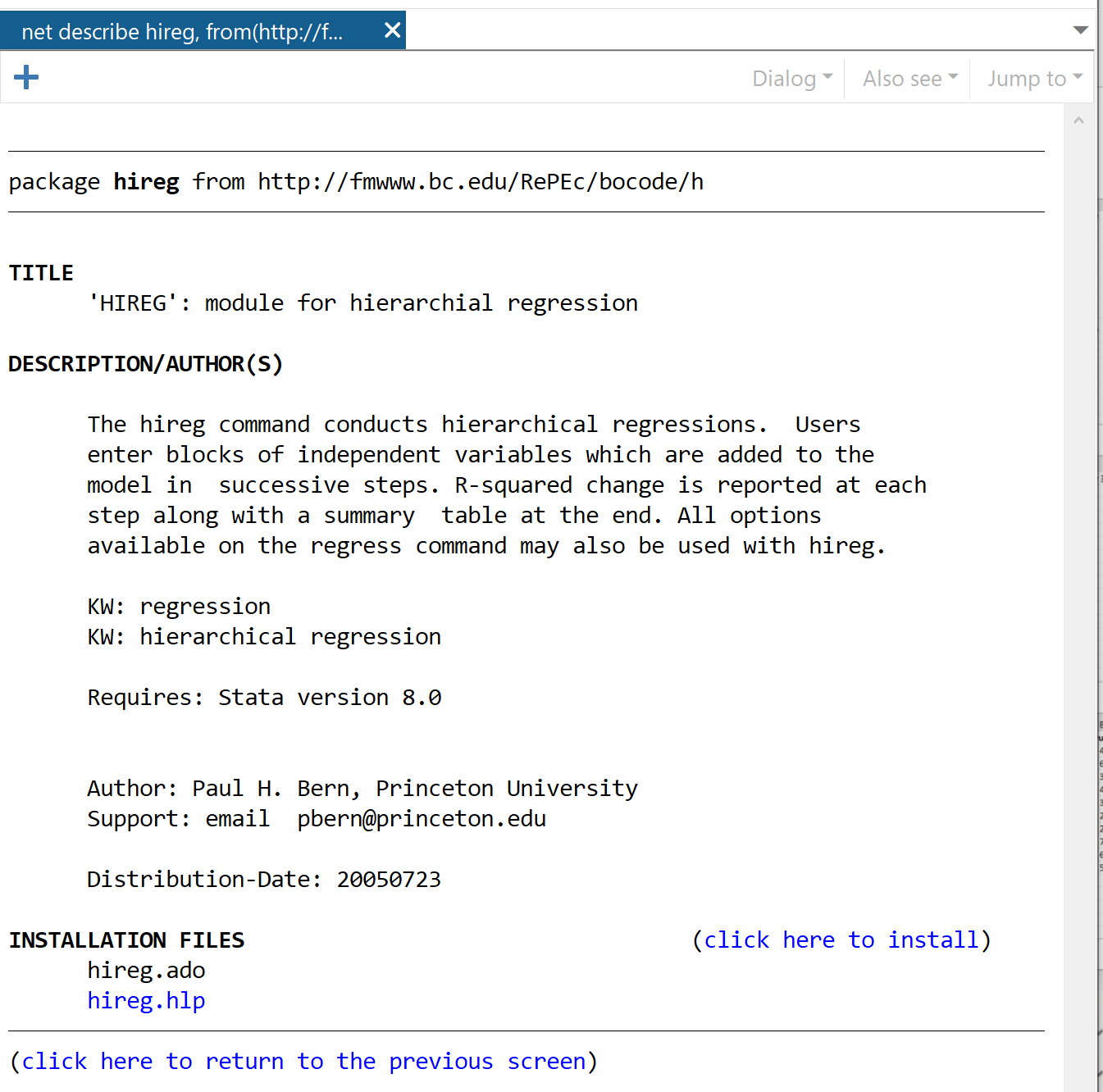
سيتم تثبيت الحزمة في ثوان. وبعد ذلك، لإجراء الانحدار الهرمي، سوف نستخدم الأمر التالي:

سعر الإيجار (ميل لكل جالون) (الوزن) (نسبة التروس)

إليك ما يطلب هذا من Stata القيام به:

• قم بإجراء الانحدار الهرمي باستخدام السعر كمتغير الاستجابة في كل نموذج.
• بالنسبة للنموذج الأول، استخدم mpg كمتغير توضيحي.
• بالنسبة للنموذج الثاني، أضف الوزن كمتغير توضيحي إضافي.
• بالنسبة للنموذج الثالث، أضف gear_ratio كمتغير توضيحي آخر.

وهذه نتيجة النموذج الأول:

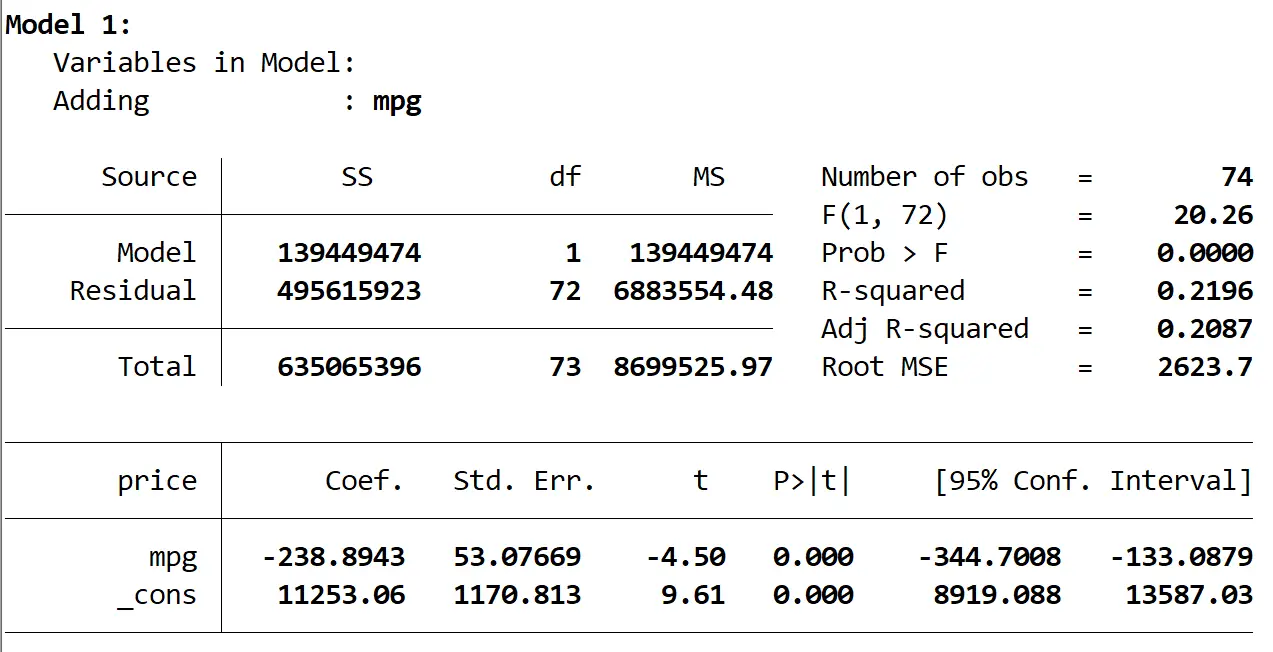
نرى أن مربع R للنموذج هو 0.2196 وأن القيمة p الإجمالية (Prob > F) للنموذج هي 0.0000 ، وهي ذات دلالة إحصائية عند α = 0.05.

وبعد ذلك نرى نتيجة النموذج الثاني:

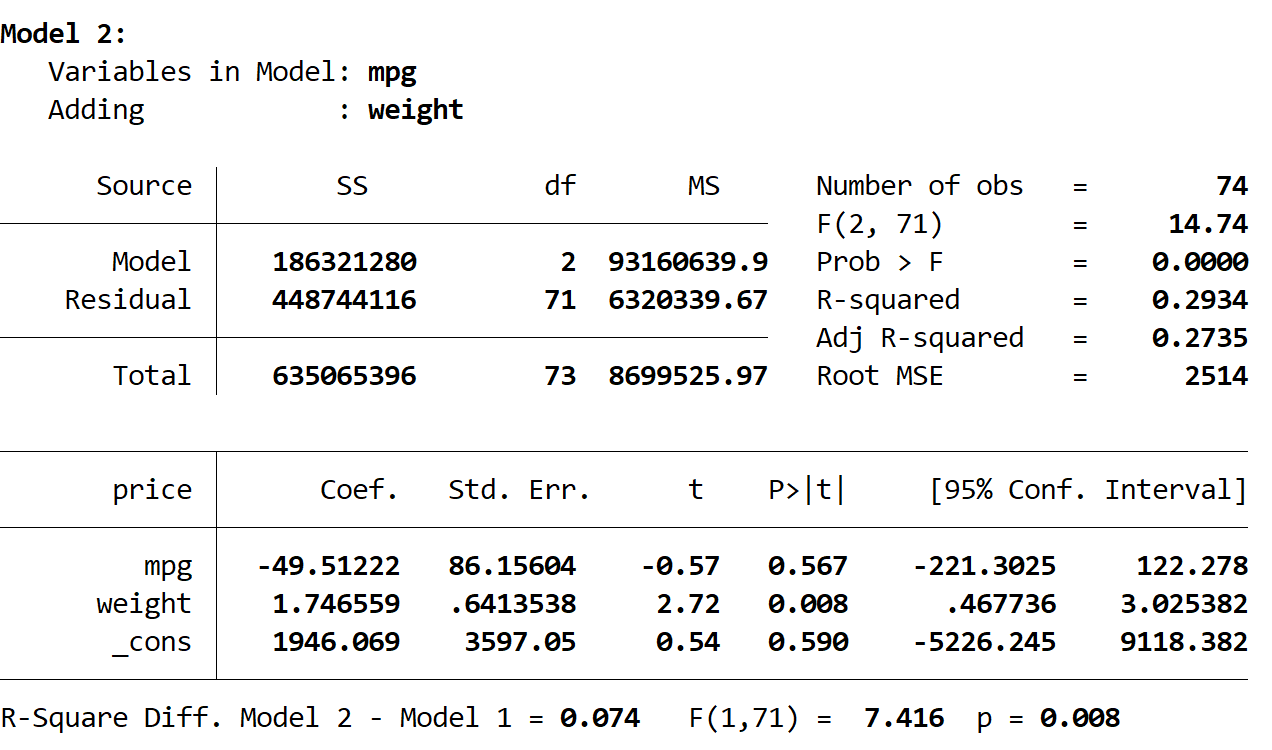
مربع R لهذا النموذج هو 0.2934 وهو أكبر من النموذج الأول. لتحديد ما إذا كان هذا الاختلاف ذا دلالة إحصائية، أجرت شركة Stata اختبار F الذي أعطى الأرقام التالية في أسفل النتيجة:

• R تربيع الفرق بين النموذجين = 0.074
• إحصائيات F للفرق = 7.416
• القيمة p المقابلة لإحصاء F = 0.008

وبما أن القيمة p أقل من 0.05، نستنتج أن هناك تحسنا معتد به إحصائيا في النموذج الثاني مقارنة بالنموذج الأول.

وأخيرا يمكننا أن نرى نتيجة النموذج الثالث:

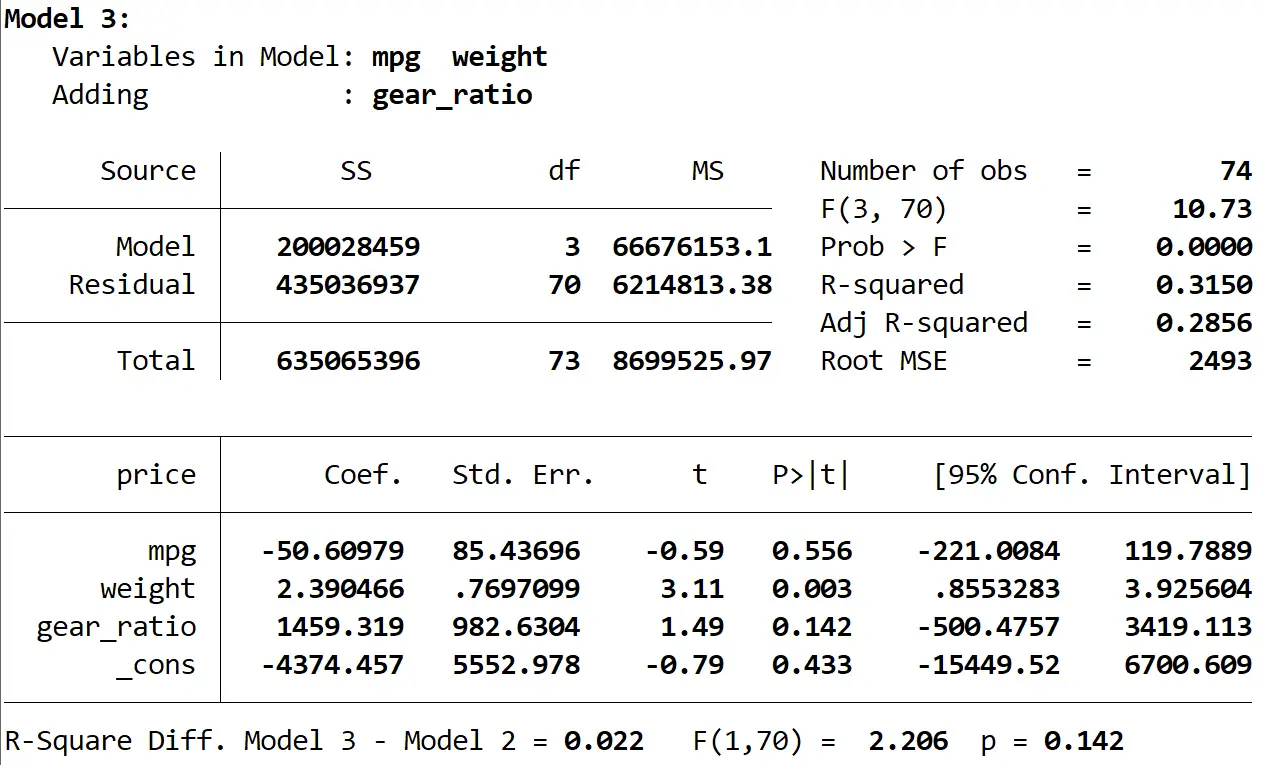
مربع R لهذا النموذج هو 0.3150 وهو أكبر من النموذج الثاني. لتحديد ما إذا كان هذا الاختلاف ذا دلالة إحصائية، أجرت شركة Stata اختبار F الذي أعطى الأرقام التالية في أسفل النتيجة:

• R تربيع الفرق بين النموذجين = 0.022
• إحصائيات F للفرق = 2.206
• المقابلة قيمة p لإحصاء F = 0.142

وبما أن القيمة p لا تقل عن 0.05، فليس لدينا أدلة كافية لنقول أن النموذج الثالث يقدم تحسنا عن النموذج الثاني.

في نهاية النتيجة، يمكننا أن نرى أن Stata تقدم ملخصًا للنتائج:

في هذا المثال بالتحديد، نستنتج أن النموذج 2 قدم تحسينًا كبيرًا عن النموذج 1، لكن النموذج 3 لم يقدم تحسينًا كبيرًا عن النموذج 2.