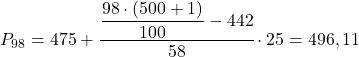النسب المئوية (الإحصائيات)
تشرح هذه المقالة ماهية النسبة المئوية وكيفية حسابها. ستجد تمارين محلولة حول النسب المئوية، وبالإضافة إلى ذلك، ستتمكن من حساب أي نسبة مئوية من عينة البيانات الخاصة بك باستخدام الآلة الحاسبة عبر الإنترنت.
ما هي النسب المئوية؟
في الإحصاء، النسب المئوية هي القيم التي تقسم مجموعة من البيانات المرتبة إلى مائة جزء متساوي. لذا، تشير النسبة المئوية إلى القيمة التي تقل عنها نسبة مئوية من مجموعة البيانات.
على سبيل المثال، القيمة المئوية الخامسة والثلاثون أعلى من 35% من البيانات المرصودة، ولكنها أقل من بقية البيانات.
يتم تمثيل النسب المئوية بالحرف الكبير P والمؤشر المئوي، أي أن المئين الأول هو P 1 ، والمئين الأربعين هو P 40 ، والمئين 79 هو P 79 ، وهكذا.

👉 يمكنك استخدام الآلة الحاسبة أدناه لحساب النسب المئوية لأي مجموعة بيانات.
وبالمثل، فإن النسب المئوية هي مقياس للوضع غير المركزي إلى جانب الربعيات والخماسيات والعشريات. يمكنك التحقق من معنى كل نوع من هذه الأنواع الكمية على موقعنا.
تجدر الإشارة إلى أن مصطلح المئين يستخدم أيضاً لمقارنة وزن الطفل وطوله مع القيم القياسية للأطفال الآخرين، حيث توجد جداول نمو ذات قيم مسجلة تساعد في تحديد ما إذا كان الطفل ينمو بشكل صحيح أم لا. . .
كيفية حساب النسب المئوية
لحساب موضع نسبة مئوية لسلسلة بيانات إحصائية، يجب عليك ضرب الرقم المئوي في مجموع إجمالي عدد نقاط البيانات بالإضافة إلى واحد وتقسيم النتيجة على مائة.
وبالتالي فإن الصيغة المئوية هي:
![]()
يرجى ملاحظة: هذه الصيغة تخبرنا بموضع النسبة المئوية، وليس قيمتها. ستكون النسبة المئوية هي البيانات الموجودة في الموضع الذي حصلت عليه الصيغة.
لكن في بعض الأحيان نتيجة هذه الصيغة تعطينا رقما عشريا، لذلك يجب علينا التمييز بين حالتين اعتمادا على ما إذا كانت النتيجة رقما عشريا أم لا:
- إذا كانت نتيجة الصيغة عبارة عن رقم بدون جزء عشري ، فإن النسبة المئوية تتوافق مع البيانات الموجودة في الموضع الذي توفره الصيغة أعلاه.
- إذا كانت نتيجة الصيغة رقمًا بجزء عشري ، فسيتم حساب القيمة المئوية الدقيقة باستخدام الصيغة التالية:
![]()
حيث x i و x i+1 هما أرقام المواضع التي يقع بينها الرقم الذي تم الحصول عليه بواسطة الصيغة الأولى، و d هو الجزء العشري من الرقم الذي تم الحصول عليه بواسطة الصيغة الأولى.
قد تظن الآن أن العثور على النسب المئوية لعينة إحصائية أو مجتمع إحصائي أمر معقد لأن الطريقة تتضمن العديد من الخطوات، ولكنها في الواقع سهلة. اقرأ المثالين الملموسين التاليين وأنا متأكد من أنك ستفهمهما بشكل أفضل.
ملاحظة : لم يتفق المجتمع العلمي بعد بشكل كامل على كيفية حساب النسب المئوية، لذا يمكنك العثور على كتاب إحصائي يشرح ذلك بشكل مختلف قليلاً.
أمثلة على حساب النسبة المئوية
كما رأيت أعلاه في شرح كيفية العثور على النسب المئوية للعينة، يختلف الحساب اعتمادًا على ما إذا كانت نتيجة الصيغة الأولى عشرية أم لا. ولهذا السبب ستجد أدناه مثالين تم حلهما، واحد لكل حالة.
مثال 1
- من البيانات الموضحة في الجدول التالي، احسب النسب المئوية الأولى والثالثة والأربعين والتاسعة والثمانين.
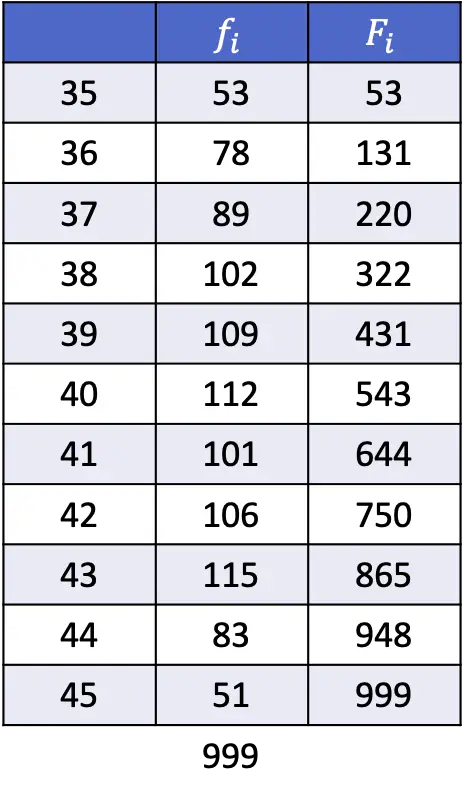
كما هو موضح في القسم السابق، فإن صيغة العثور على موضع النسبة المئوية هي:
![]()
في هذه الحالة، حجم العينة لهذا التمرين هو 999 بيانات إحصائية، لذا لحساب موضع المئين الأول نحتاج إلى استبدال 999 بـ n و1 بـ k :
![]()
لذا فإن النسبة المئوية الأولى ستكون تلك التي يكون تكرارها المطلق التراكمي أكبر من 10 مباشرة، وهو في هذه الحالة 35 نظرًا لأن تكرارها المطلق التراكمي يساوي 53.
لتحديد النسبة المئوية 43، يجب عليك استخدام نفس الصيغة، ولكن من الواضح أننا هذه المرة نستبدل k بـ 43.
![]()
التكرار التراكمي المطلق الذي يزيد مباشرة عن 430 هو 431 من البيانات 39، وبالتالي فإن النسبة المئوية 43 تساوي 39.
وأخيرًا، نطبق نفس الصيغة للحصول على النسبة المئوية 89:
![]()
التكرار المطلق التراكمي للقيمة 44 هو 948، وهو أكبر مباشرة من 890. وبالتالي، فإن النسبة المئوية 89 هي 44.
مثال 2
- أوجد النسبتين المئويتين 35 و67 لسلسلة البيانات التالية:
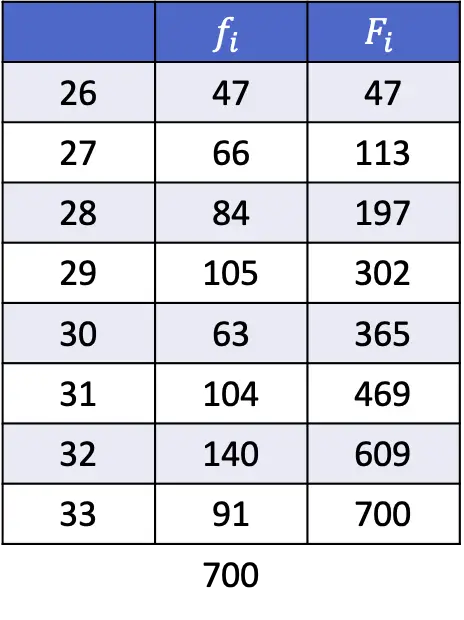
حتى لو كان علينا إجراء المزيد من العمليات الحسابية في هذا التمرين، فإن المبدأ لا يزال كما هو: يجب علينا حساب الموضع المئوي بالتعبير التالي.
![]()
وبالتالي، لحساب النسبة المئوية الخامسة والثلاثين، نستبدل k بـ 35 و n بإجمالي عدد البيانات، أي 700:
![]()
لكن هذه المرة حصلنا على رقم عشري من الصيغة، لذا نحتاج إلى تطبيق التعبير الجبري التالي لحساب القيمة المئوية الدقيقة:
![]()
الرقم الذي تعطيه الصيغة الأولى هو 245.35، وبالتالي فإن النسبة المئوية 35 تقع بين الموضعين 245 و246، وهو ما يتوافق مع القيمتين 29 و29 على التوالي. لذلك، x i يساوي 29، x i+1 يساوي 29 و d يساوي الجزء العشري من الرقم الذي تم الحصول عليه، أي 0.35.
![]()
ولإيجاد النسبة المئوية 67، علينا استخدام الطريقة نفسها. نحسب أولاً الموضع المئوي:
![]()
يشير الرقم الناتج 469.67 إلى أن النسبة المئوية ستكون بين الموضعين 469 و470، وقيمتها 31 و32. لذلك، نستخدم الصيغة الثانية في العملية للعثور على القيمة المئوية الدقيقة:
![]()
آلة حاسبة مئوية
أدخل مجموعة بيانات إحصائية والرقم المئوي الذي تريد حسابه في الآلة الحاسبة التالية. يجب فصل البيانات بمسافة وإدخالها باستخدام النقطة كفاصل عشري.
النسب المئوية في البيانات المجمعة
لحساب النسب المئوية عند تجميع البيانات في مجموعات ، نحتاج أولاً إلى العثور على المجموعة أو الفئة التي تقع فيها النسبة المئوية باستخدام الصيغة التالية:
![]()
وبالتالي فإن النسبة المئوية ستكون في الفترة التي يكون تكرارها المطلق أكبر مباشرة من الرقم الذي تم الحصول عليه في التعبير السابق.
وبمجرد أن نعرف بالفعل الفاصل الزمني الذي تنتمي إليه النسبة المئوية، يجب علينا تطبيق الصيغة التالية للعثور على القيمة الدقيقة للشريحة المئوية:
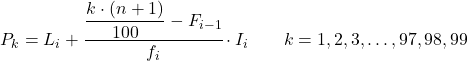
ذهب:
- L i هو الحد الأدنى للفاصل الزمني الذي تقع فيه النسبة المئوية.
- n هو العدد الإجمالي للملاحظات.
- F i-1 هو التردد المطلق التراكمي للفاصل الزمني السابق.
- f i هو التكرار المطلق للفاصل الزمني الذي تقع فيه النسبة المئوية.
- I i هو عرض الفاصل الزمني المئوي.
فيما يلي تمرين خطوة بخطوة حول كيفية الحصول على النسب المئوية عند التعبير عن البيانات على فترات. على وجه التحديد، يتم حساب النسب المئوية 29 و52 و98.

تم تجميع البيانات في هذه العينة كفواصل زمنية، لذلك نحتاج إلى القيام بخطوتين لتحديد النسب المئوية: نحتاج أولاً إلى العثور على الفاصل الزمني الذي يقع فيه المئين، ثم تطبيق الصيغة لحساب القيمة الدقيقة للشريحة المئوية. النسبة المئوية.
وهكذا نجد موضع المئين التاسع والعشرين بالتعبير التالي:
![]()
![]()
ستكون الفترة المئوية هي التي يكون تكرارها المطلق التراكمي أكبر مباشرة من 145.29، وهي في هذه الحالة هي الفترة [350.375) التي يكون ترددها المطلق التراكمي 175. وبمجرد أن نعرف الفاصل المئوي، نطبق الصيغة التالية لحسابها القيمة الدقيقة:
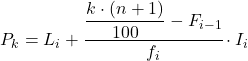
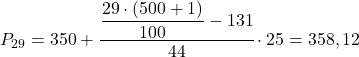
والآن نكرر نفس الإجراء لحساب النسبة المئوية الثانية والخمسين. نحسب أولاً الفاصل الزمني:
![]()
الفاصل المئوي 52 هو [400.425) لأن تردده المطلق التراكمي (298) هو أعلى مباشرة من 260.52. وبالتالي فإن القيمة الدقيقة للنسبة المئوية ستكون:
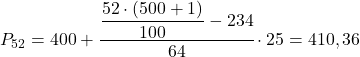
وأخيرا، سوف نجد النسبة المئوية 98. وكما هو الحال دائمًا، نحسب أولاً الفاصل الزمني الذي يقع فيه:
![]()
وبمجرد أن نعرف الفترة التي تقع فيها النسبة المئوية، نحسب قيمتها الدقيقة باستخدام الصيغة التالية: