اختبار تناسب مربع كاي على الآلة الحاسبة ti-84

يتم استخدام اختبار جودة الملاءمة لمربع كاي لتحديد ما إذا كان المتغير القاطع يتبع توزيعًا افتراضيًا أم لا.

يشرح هذا البرنامج التعليمي كيفية إجراء اختبار تناسب مربع كاي على الآلة الحاسبة TI-84.

مثال: اختبار تناسب مربع كاي على الآلة الحاسبة TI-84

يقول صاحب متجر إن عددًا متساويًا من العملاء يأتون إلى متجره كل يوم من أيام الأسبوع. لاختبار هذه الفرضية، يقوم باحث مستقل بتسجيل عدد العملاء الذين يأتون إلى المتجر في أسبوع معين ويجد ما يلي:

• الاثنين: 50 عميلاً
• الثلاثاء: 60 عميلاً
• الأربعاء: 40 عميلاً
• الخميس: 47 عميلاً
• الجمعة: 53 عميلاً

سوف نستخدم الخطوات التالية لإجراء اختبار مدى ملاءمة مربع كاي لتحديد ما إذا كانت البيانات متوافقة مع مطالبة مالك المتجر.

الخطوة 1: أدخل البيانات.

أولاً سوف نقوم بإدخال قيم البيانات الخاصة بعدد العملاء المتوقع كل يوم وعدد العملاء الملحوظ كل يوم. اضغط على Stat ثم اضغط على EDIT . أدخل القيم التالية لعدد العملاء الملحوظ في العمود L1 وقيم العدد المتوقع للعملاء في العمود L2:

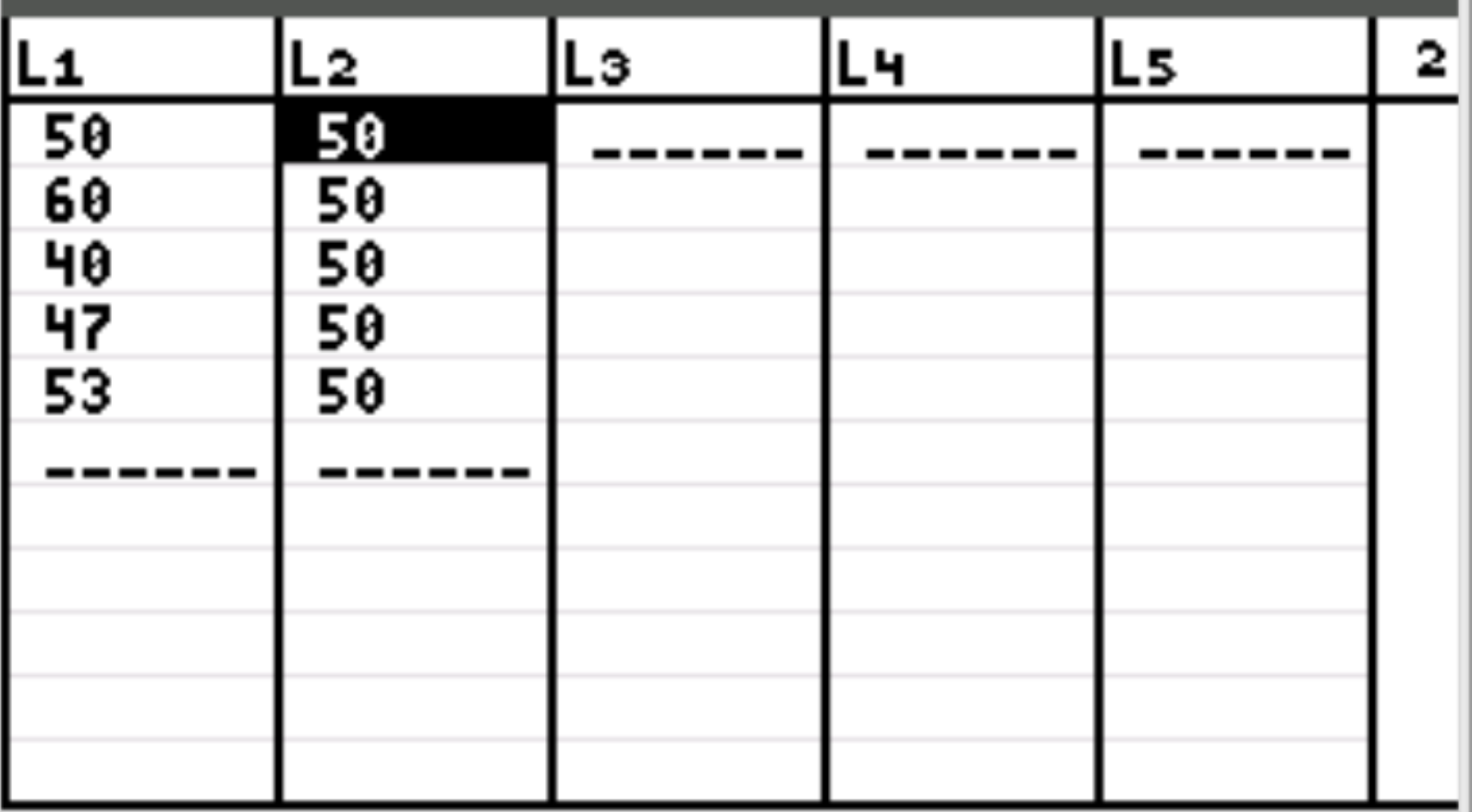
ملاحظة: كان هناك 250 عميلا في المجموع. لذلك، إذا كان صاحب المتجر يتوقع دخول عدد متساوٍ من العملاء إلى المتجر يوميًا، فسيكون ذلك 50 عميلًا يوميًا.

الخطوة 2: إجراء اختبار جودة المطابقة لمربع كاي.

بعد ذلك، سنقوم بإجراء اختبار جودة المطابقة لمربع كاي. اضغط على Stat ثم قم بالتمرير إلى TESTS . ثم قم بالتمرير لأسفل إلى X ² GOF-Test واضغط على Enter .

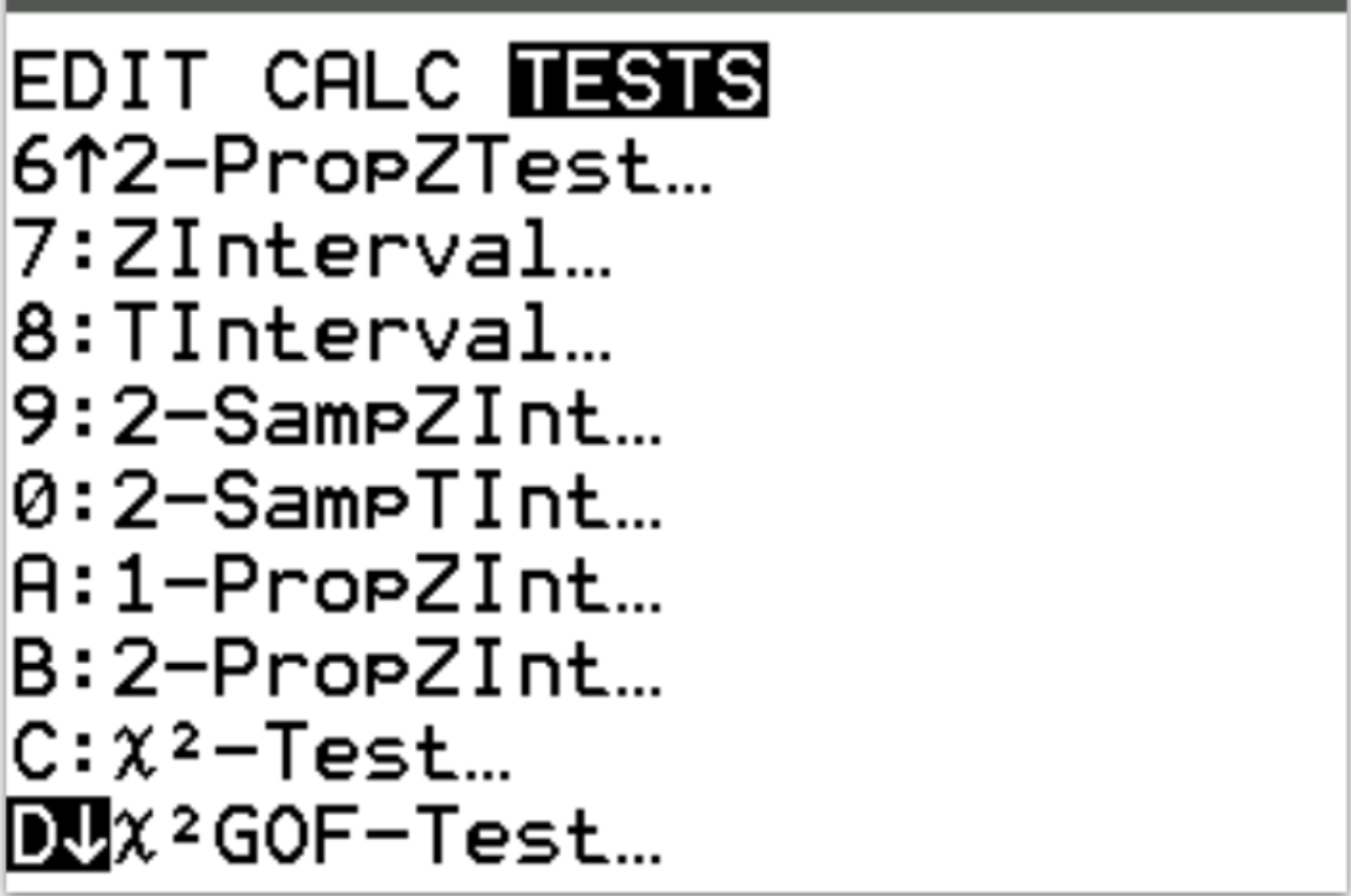
بالنسبة للملاحظة ، اختر قائمة L1. بالنسبة للمتوقع ، اختر قائمة L2. بالنسبة إلى df (درجات الحرية)، أدخل #categories – 1. في حالتنا لدينا 5-1 = 4. ثم قم بتمييز “حساب” واضغط على “Enter” .

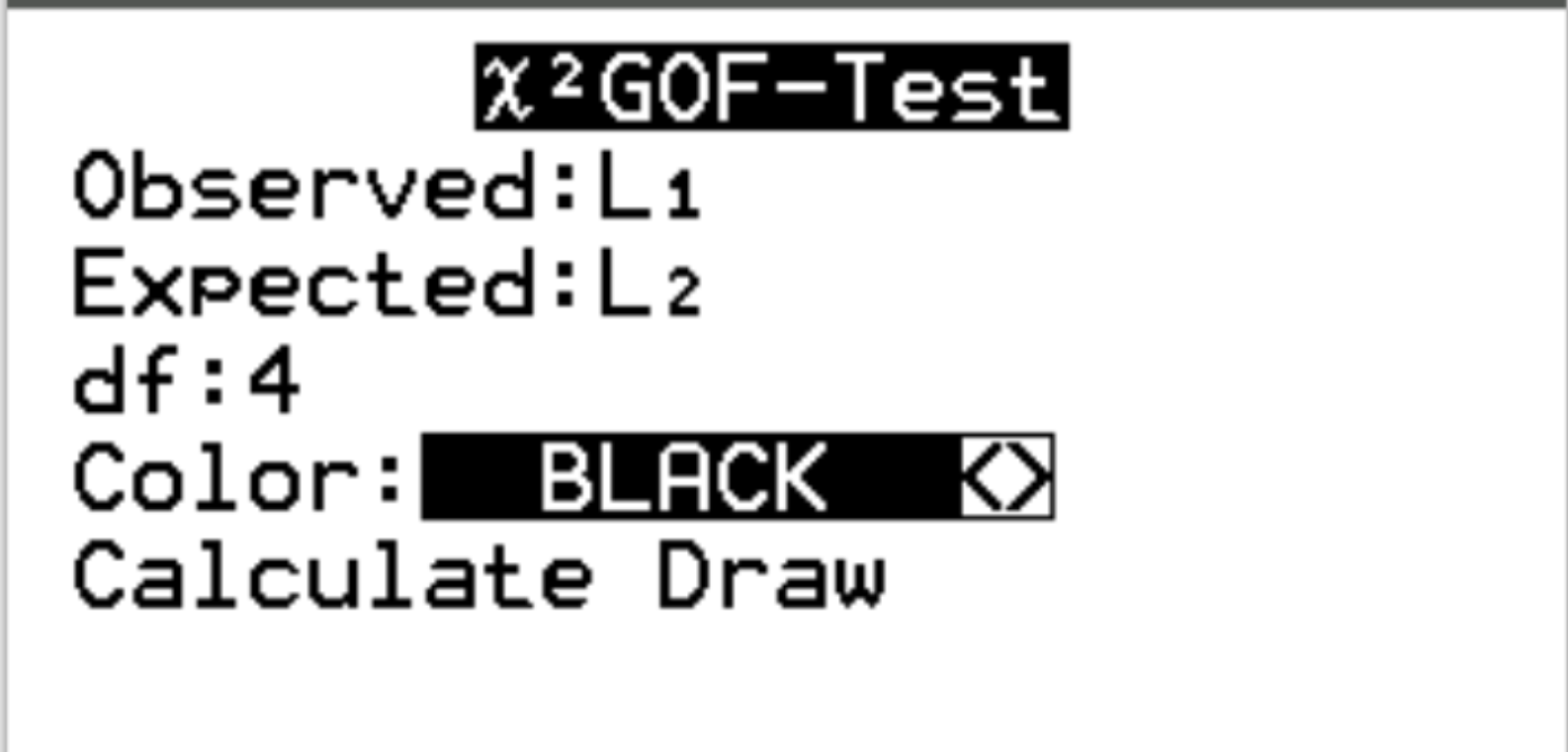
سيظهر الإخراج التالي تلقائيًا:

الخطوة 3: تفسير النتائج.

إحصائيات اختبار ^X2 للاختبار هي 4.36 والقيمة p المقابلة هي 0.3595 . وبما أن هذه القيمة p لا تقل عن 0.05، فإننا نفشل في رفض فرضية العدم. وهذا يعني أنه ليس لدينا ما يكفي من الأدلة لنقول أن التوزيع الحقيقي للعملاء يختلف عن ذلك الذي أبلغ عنه صاحب المتجر.