كيفية حساب الاحتمالات ذات الحدين على الآلة الحاسبة ti-84

يعد التوزيع ذو الحدين أحد التوزيعات الأكثر استخدامًا في جميع الإحصائيات. يشرح هذا البرنامج التعليمي كيفية استخدام الوظائف التالية على الآلة الحاسبة TI-84 للعثور على احتمالات ذات الحدين:

تُرجع binompdf(n, p, x) الاحتمالية المرتبطة بملف pdf ذي الحدين.

تُرجع binomcdf(n, p, x) الاحتمال التراكمي المرتبط بـ cdf ذي الحدين.

ذهب:

• ن = عدد التجارب
• ع = احتمال النجاح في تجربة معينة
• س = إجمالي عدد النجاحات

يمكن الوصول إلى هاتين الوظيفتين على الآلة الحاسبة TI-84 بالضغط على 2nd ثم الضغط على vars . سينقلك هذا إلى شاشة DISTR حيث يمكنك بعد ذلك استخدام binompdf() و binomcdf() :

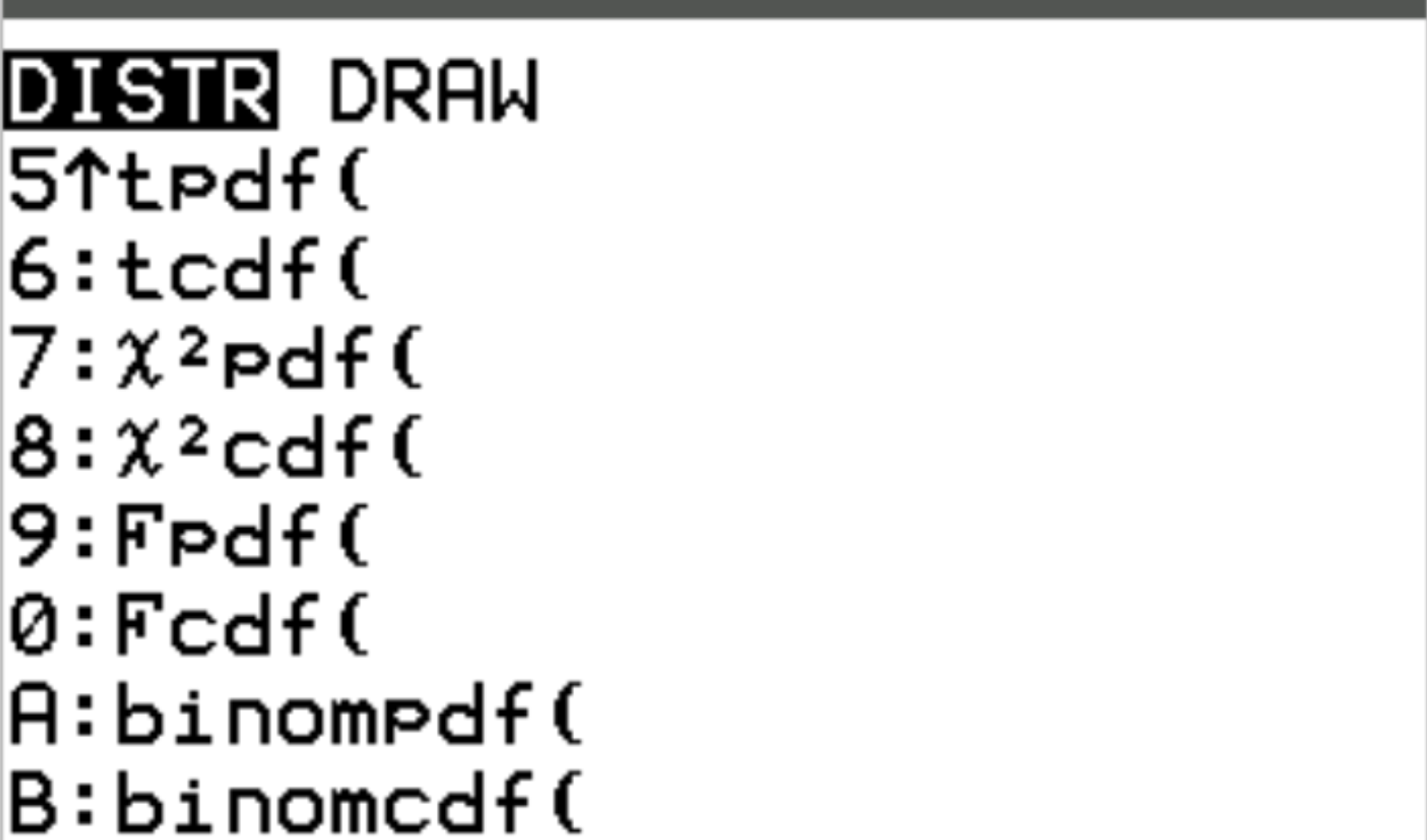
توضح الأمثلة التالية كيفية استخدام هذه الوظائف للإجابة على أسئلة مختلفة.

مثال 1: الاحتمال ذو الحدين لنجاح x بالضبط

سؤال: يقوم ناثان بنسبة 60% من محاولات الرمية الحرة. إذا نفذ 12 رمية حرة، فما احتمال أن ينفذ 10 رميات بالضبط؟

الإجابة: استخدم الدالة binomialpdf(n, p, x):

ذات الحدينpdf(12, .60, 10) = 0.0639

مثال 2: احتمال ذو الحدين أقل من نجاح x

سؤال: يقوم ناثان بنسبة 60% من محاولات الرمية الحرة. إذا نفذ 12 رمية حرة، فما احتمال أن يكون أقل من 10؟

الإجابة: استخدم الدالة ذات الحدين cdf(n, p, x-1) :

ذات الحدين cdf(12, .60, 9) = 0.9166

مثال 3: احتمال ذو الحدين لنجاح x على الأكثر

سؤال: يقوم ناثان بنسبة 60% من محاولات الرمية الحرة. إذا نفذ 12 رمية حرة، فما احتمال أن ينفذ 10 رميات على الأكثر؟

الإجابة: استخدم الدالة ذات الحدين cdf(n, p, x) :

ذات الحدين cdf(12, .60, 10) = 0.9804

مثال 4: احتمال ذو الحدين لأكثر من x نجاحات

سؤال: يقوم ناثان بنسبة 60% من محاولات الرمية الحرة. إذا نفذ 12 رمية حرة، فما احتمال أن ينفذ أكثر من 10 رميات؟

الإجابة: استخدم الوظيفة 1 – binomialcdf(n, p, x) :

1 – ذو الحدين cdf(12، .60، 10) = 0.0196

مثال 5: احتمال ذو الحدين لنجاح x على الأقل

سؤال: يقوم ناثان بنسبة 60% من محاولات الرمية الحرة. إذا نفذ 12 رمية حرة، فما احتمال أن ينفذ أكثر من 10 رميات؟

الإجابة: استخدم الدالة 1 – binomialcdf(n, p, x-1) :

1 – ذو الحدين cdf(12, .60, 9) = 0.0834