فارق متوسط
تشرح هذه المقالة معنى الانحراف وكيفية حسابه. ستجد أيضًا أمثلة ملموسة لحساب متوسط الانحراف. علاوة على ذلك، ستتمكن من حساب متوسط الانحراف لأي مجموعة بيانات إحصائية باستخدام الآلة الحاسبة عبر الإنترنت.
ما هو يعني الانحراف؟
متوسط الانحراف ، ويسمى أيضًا متوسط الانحراف المطلق ، هو مقياس للتشتت الإحصائي.
متوسط الانحراف لمجموعة البيانات هو متوسط الانحرافات المطلقة . ولذلك، فإن متوسط الانحراف يساوي مجموع انحرافات كل عنصر بيانات عن الوسط الحسابي مقسومًا على إجمالي عدد عناصر البيانات.
وبعبارة أخرى، فإن صيغة متوسط الانحراف هي كما يلي:

👉 يمكنك استخدام الآلة الحاسبة أدناه لحساب متوسط الانحراف لأي مجموعة بيانات.
في الإحصاء، يُسمى متوسط الانحراف أيضًا متوسط الانحراف المطلق .
ويتم تفسير متوسط الانحراف على النحو التالي: كلما زادت قيمة متوسط الانحراف، يعني ذلك أن البيانات، في المتوسط، أبعد عن الوسط الحسابي؛ وعلى العكس من ذلك، كلما انخفض متوسط الانحراف، كلما كانت القيمة أقرب. البيانات هي. وبالتالي فإن متوسط الانحراف يشير إلى تشتت سلسلة البيانات.
المقاييس الأخرى التي تعتبر موزعة هي المدى، المدى الربيعي، الانحراف المعياري (أو الانحراف المعياري)، التباين، ومعامل التباين.
كيفية حساب متوسط الانحراف
لحساب متوسط الانحراف لسلسلة البيانات، يجب اتباع الخطوات التالية:
- احسب الوسط الحسابي لمجموعة البيانات الإحصائية.
- احسب انحراف كل نقطة بيانات عن المتوسط، والذي يعرف بالقيمة المطلقة للفرق بين البيانات والمتوسط.
- أضف جميع الاختلافات المحسوبة في الخطوة السابقة.
- قسّم على إجمالي عدد البيانات. والنتيجة التي تم الحصول عليها هي متوسط الانحراف لسلسلة البيانات.
وباختصار، فإن الصيغة التي يجب تطبيقها للعثور على متوسط الانحراف هي:
![]()
مثال لحساب متوسط الانحراف
وبالنظر إلى تعريف متوسط الانحراف، يوجد أدناه مثال تم حله خطوة بخطوة لحساب متوسط الانحراف لعينة إحصائية. بهذه الطريقة ستفهم بشكل أفضل كيفية الحصول على متوسط الانحراف.
- يقوم أحد المحللين بدراسة النتائج الاقتصادية لشركة ما خلال العام الماضي ولديه معلومات عن الأرباح التي حققتها الشركة خلال كل ربع من العام المذكور: 2، 3، 7 و5 مليون دولار. ما هو متوسط انحراف البيانات؟
أولاً، نحتاج إلى حساب متوسط البيانات، فنجمعها ونقسمها على إجمالي عدد الملاحظات (4):
![]()
بمجرد حساب المتوسط الحسابي، نستخدم صيغة انحراف المتوسط:
![]()
نعوض البيانات في الصيغة:
![]()
نقوم بالحسابات في البسط:
![]()
![]()
![]()
وأخيرًا نقسم على إجمالي عدد البيانات للحصول على متوسط انحراف العينة:
![]()
حاسبة متوسط الانحراف
أدخل مجموعة من البيانات الإحصائية في الآلة الحاسبة التالية لحساب متوسط انحرافها. يجب فصل البيانات بمسافة وإدخالها باستخدام النقطة كفاصل عشري.
متوسط الانحراف للبيانات المجمعة
لحساب متوسط الانحراف للبيانات المجمعة في فواصل زمنية، يجب اتباع الخطوات التالية:
- تحديد الوسط الحسابي لمجموعة البيانات الإحصائية. وبما أن البيانات مجمعة، فإن التعبير لحساب المتوسط هو:
- احسب انحراف كل فترة عن المتوسط، وهو ما يعادل القيمة المطلقة للفرق بين درجة الفصل والمتوسط.
- اضرب انحراف كل فترة في تكرارها المطلق.
- اجمع كل نتائج الخطوة السابقة، ثم اقسمها على إجمالي عدد البيانات. والنتيجة التي تم الحصول عليها هي متوسط انحراف العينة المجمعة في فترات.
![]()
![]()
![]()
![]()
في الختام، فإن صيغة الحصول على متوسط الانحراف من البيانات المجمعة هي:
![]()
عندما يتم تجميع البيانات، فهذا يعني عادةً أن هناك الكثير من البيانات، ويتطلب العثور على متوسط الانحراف العديد من الخطوات. ولذلك، عادة ما تستخدم الجداول التكرارية لإجراء الحساب.
فيما يلي تمرين خطوة بخطوة حول كيفية حساب متوسط الانحراف عند تجميع البيانات في فواصل زمنية:
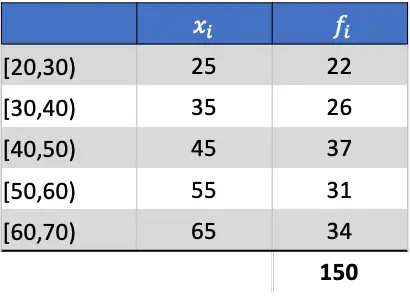
أول شيء يجب فعله هو حساب متوسط البيانات المجمعة. للقيام بذلك، نضيف عمودًا إلى الجدول عن طريق ضرب ملاحظة الفصل في تكرارها:
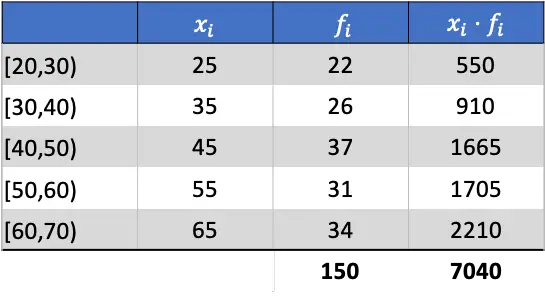
وبالتالي فإن الوسط الحسابي سيكون نتيجة قسمة مجموع العمود المضاف على مجموع التكرارات المطلقة:
![]()
الآن بعد أن عرفنا متوسط البيانات، يمكننا إضافة جميع الأعمدة اللازمة للعثور على متوسط الانحراف:
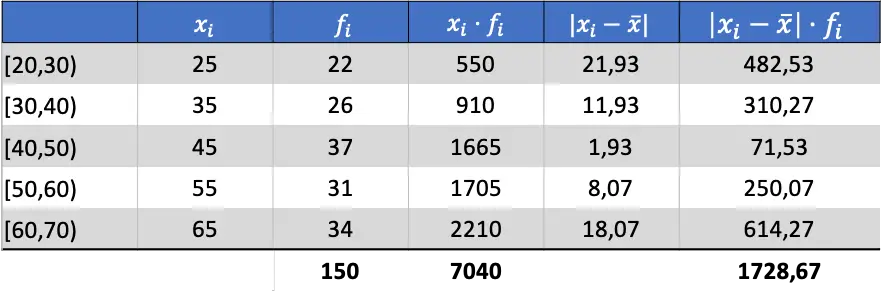
وبالتالي، للحصول على متوسط الانحراف يجب عليك قسمة مجموع العمود الأخير على إجمالي عدد الملاحظات:
![]()