مقدمة لتوزيع بواسون

توزيع بواسون هو أحد التوزيعات الأكثر شعبية في الإحصاء.

لفهم توزيع بواسون، من المفيد أن نفهم أولاً تجارب بواسون.

تجارب الأسماك

تجربة بواسون هي تجربة لها الخصائص التالية:

• يمكن حساب عدد نجاحات التجربة.
• يُعرف متوسط عدد النجاحات التي حدثت خلال فترة زمنية (أو مساحة) محددة.
• كل نتيجة مستقلة.
• يتناسب احتمال حدوث النجاح مع حجم الفاصل الزمني.

مثال على تجربة بواسون هو عدد الولادات في الساعة في مستشفى معين. على سبيل المثال، لنفترض أن متوسط عدد الولادات في مستشفى معين هو 10 ولادات في الساعة. هذه تجربة بواسون لأنها تحتوي على الخصائص الأربع التالية:

• يمكن إحصاء عدد نجاحات التجربة – يمكننا إحصاء عدد الولادات.
• معرفة متوسط عدد الولادات التي تتم خلال فترة زمنية محددة – من المعلوم أن هناك في المتوسط 10 ولادات في الساعة.
• كل نتيجة مستقلة – احتمال أن تلد أم واحدة في ساعة معينة مستقل عن احتمال أن تلد أم أخرى.
• يتناسب احتمال حدوث النجاح مع حجم الفاصل الزمني: كلما زاد الفاصل الزمني، زاد احتمال حدوث الولادة.

يمكننا استخدام توزيع بواسون للإجابة عن الأسئلة المتعلقة باحتمالات تجربة بواسون مثل:

• ما هو احتمال حدوث أكثر من 12 ولادة في ساعة معينة؟
• ما هو احتمال حدوث أقل من 5 ولادات في ساعة معينة؟
• ما هو احتمال حدوث ما بين 8 و 11 ولادة في ساعة معينة؟

توزيع الأسماك

يصف توزيع بواسون احتمالية الحصول على نجاحات k خلال فترة زمنية معينة.

إذا كان المتغير العشوائي X يتبع توزيع بواسون، فيمكن العثور على احتمال نجاح X = k من خلال الصيغة التالية:

P(X=k) =  ^ك * ه ^{– } / ك!

ذهب:

• : متوسط عدد النجاحات التي تحدث خلال فترة زمنية محددة
• ك: عدد النجاحات
• e: ثابت يساوي 2.71828 تقريبًا

على سبيل المثال، لنفترض أن مستشفى معين يشهد معدل ولادتين في الساعة. يمكننا استخدام الصيغة أعلاه لتحديد احتمالية حدوث 0، 1، 2، 3 ولادات، وما إلى ذلك. في ساعة معينة:

P(X=0) = 2 ⁰ * ه ^{– 2} / 0! = 0.1353

P(X=1) = 2 ¹ * ه ^{– 2} / 1! = 0.2707

ع(X=2) = 2 ² * ه ^{– 2} / 2! = 0.2707

ع(X=3) = 2 ³ * ه ^{– 2} / 3! = 0.1805

يمكننا حساب احتمالية أي عدد من الولادات حتى ما لا نهاية. نقوم بعد ذلك بإنشاء رسم بياني بسيط لتصور هذا التوزيع الاحتمالي:

حساب احتمالات بواسون التراكمية

من السهل حساب احتمال بواسون واحد (على سبيل المثال، احتمال أن يشهد المستشفى 3 ولادات في ساعة معينة) باستخدام الصيغة أعلاه، ولكن لحساب احتمالات بواسون التراكمية نحتاج إلى إضافة الاحتمالات الفردية.

على سبيل المثال، لنفترض أننا نريد معرفة احتمالية حدوث ولادة واحدة أو أقل في المستشفى خلال ساعة معينة. سوف نستخدم الصيغة التالية لحساب هذا الاحتمال:

ف (X ≥1) = ف (X = 0) + ف (X = 1) = 0.1353 + 0.2707 = 0.406

وهذا ما يسمى بالاحتمال التراكمي لأنه يتضمن إضافة احتمالات متعددة. يمكننا حساب الاحتمال التراكمي لحدوث ولادة k أو أقل في ساعة معينة باستخدام صيغة مماثلة:

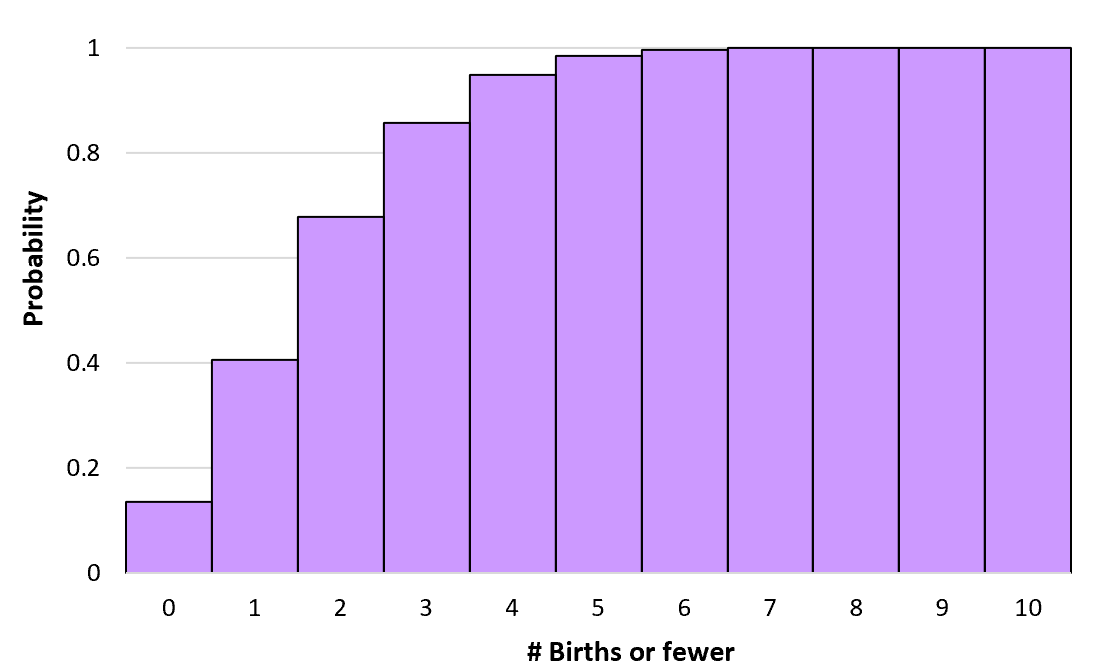
ف(X≥0) = ف(X=0) = 0.1353

ف (X ≥1) = ف (X = 0) + ف (X = 1) = 0.1353 + 0.2707 = 0.406

P(X≤2) = P(X=0) + P(X=1) + P(X=2) =0.1353 + 0.2707 + 0.2707 = 0.6767

يمكننا حساب هذه الاحتمالات التراكمية لأي عدد من الولادات حتى ما لا نهاية. يمكننا بعد ذلك إنشاء رسم بياني لتصور هذا التوزيع الاحتمالي التراكمي:

خصائص توزيع بواسون

يتميز توزيع بواسون بالخصائص التالية:

متوسط التوزيع هو π .

تباين التوزيع هو أيضا .

الانحراف المعياري للتوزيع هو √ lect .

على سبيل المثال، لنفترض أن المستشفى يسجل معدل ولادتين في الساعة.

متوسط عدد الولادات المتوقعة في ساعة معينة هو 2 = 2 مولود.

التباين في عدد الولادات التي نتوقعها هو 2 = 2 مولود.

مشاكل ممارسة توزيع الأسماك

استخدم المسائل التدريبية التالية لاختبار معرفتك بتوزيع بواسون.

ملحوظة: سوف نستخدم حاسبة توزيع بواسون لحساب إجابات هذه الأسئلة.

المشكلة 1

سؤال: نحن نعلم أن موقع ويب معين يحقق 10 مبيعات في الساعة. في ساعة معينة، ما هو احتمال أن يقوم الموقع بإجراء 8 عمليات بيع بالضبط؟

الإجابة: باستخدام حاسبة توزيع بواسون مع lect = 10 و x = 8، نجد أن P(X=8) = 0.1126 .

المشكلة 2

سؤال: نحن نعلم أن وكيل عقاري معين يقوم بمتوسط 5 مبيعات شهريًا. في شهر معين، ما هو احتمال أن تقوم بأكثر من 7 عمليات بيع؟

الإجابة: باستخدام حاسبة توزيع بواسون مع lect = 5 و x = 7، نجد أن P(X>7) = 0.13337 .

المشكلة 3

سؤال: نعلم أن مستشفى معين يشهد 4 ولادات في الساعة. في ساعة معينة، ما هو احتمال أن يكون هناك 4 ولادات أو أقل؟

الإجابة: باستخدام حاسبة توزيع بواسون مع lect = 4 و x = 4، نجد أن P(X≥4) = 0.62884 .

مصادر إضافية

تشرح المقالات التالية كيفية استخدام توزيع بواسون في برامج إحصائية مختلفة:

كيفية استخدام توزيع بواسون في R
كيفية استخدام توزيع بواسون في إكسيل
كيفية حساب احتمالات بواسون على الآلة الحاسبة TI-84
أمثلة واقعية لتوزيع بواسون
حاسبة توزيع الأسماك