مقدمة للتوزيع الهندسي

يصف التوزيع الهندسي احتمالية مواجهة عدد معين من حالات الفشل قبل تجربة النجاح الأول في سلسلة من تجارب برنولي.

تجربة برنولي هي تجربة ذات نتيجتين محتملتين فقط – “النجاح” أو “الفشل” – واحتمال النجاح هو نفسه في كل مرة يتم فيها إجراء التجربة.

مثال على مقال برنولي هو رمي العملة. لا يمكن للعملة أن تستقر إلا على وجهين (قد نطلق على الصورة “ضربة” والوجه “فشل”) واحتمال النجاح في كل رمية هو 0.5، على افتراض أن العملة عادلة.

إذا كان المتغير العشوائي X يتبع توزيعًا هندسيًا، فيمكن إيجاد احتمالية حدوث حالات فشل k قبل تجربة النجاح الأول من خلال الصيغة التالية:

P(X=k) = (1-p) ^kp

ذهب:

• ك: عدد حالات الفشل قبل النجاح الأول
• ع: احتمال النجاح في كل تجربة

على سبيل المثال، لنفترض أننا نريد معرفة عدد المرات التي يتعين علينا فيها رمي عملة معدنية حتى تظهر الصورة. يمكننا استخدام الصيغة أعلاه لتحديد احتمالية حدوث 0، 1، 2، 3 حالات فشل، وما إلى ذلك. قبل أن تهبط العملة على الرؤوس:

ملحوظة: يمكن أن تواجه العملة 0 “فشل” إذا ظهرت عليها صورة عند الرمية الأولى.

P(X=0) = (1-.5) ⁰ (.5) = 0.5

P(X=1) = (1-.5) ¹ (.5) = 0.25

P(X=2) = (1-.5) ² (.5) = 0.125

ف(X=3) = (1-0.5) ³ (0.5) = 0.0625

يمكننا حساب احتمال رمي أي عدد من العملات المعدنية حتى ما لا نهاية. نقوم بعد ذلك بإنشاء رسم بياني بسيط لتصور هذا التوزيع الاحتمالي:

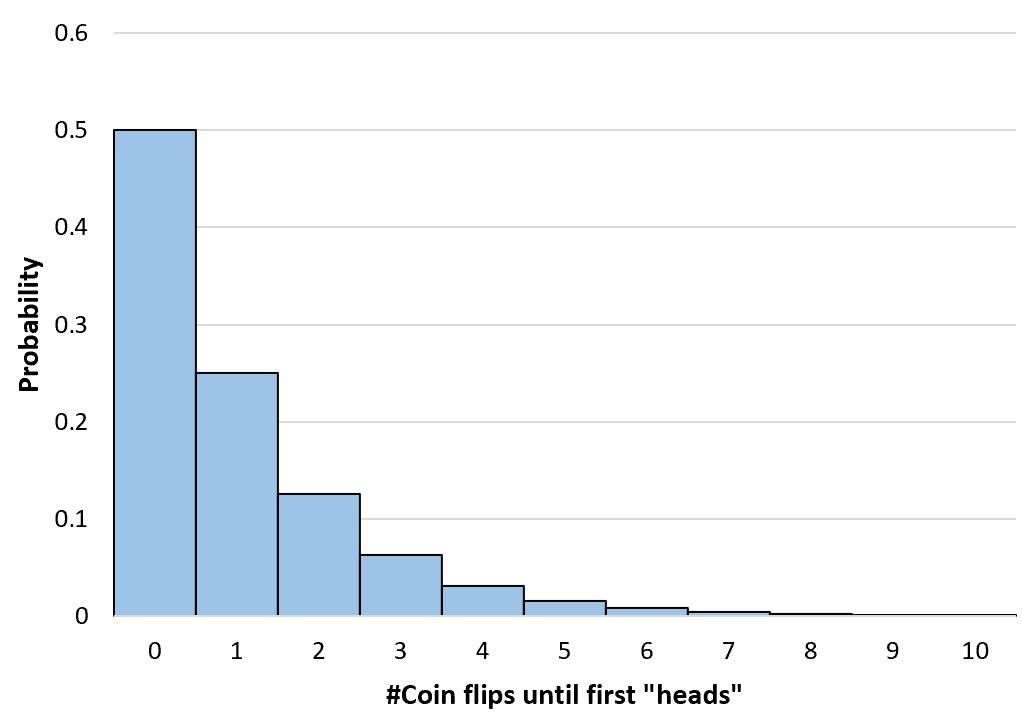
حساب الاحتمالات الهندسية التراكمية

يمكن العثور على الاحتمال التراكمي الذي نواجهه k أو أقل من حالات الفشل حتى النجاح الأول من خلال الصيغة التالية:

P(X≥k) = 1 – (1-p) ^k+1

ذهب:

• ك: عدد حالات الفشل قبل النجاح الأول
• ع: احتمال النجاح في كل تجربة

على سبيل المثال، لنفترض أننا نريد معرفة احتمال أن يستغرق الأمر ثلاث مرات “إخفاق” أو أقل قبل أن تهبط العملة أخيرًا على الوجه. سوف نستخدم الصيغة التالية لحساب هذا الاحتمال:

ف(X≥3) = 1 – (1-0.5) ³⁺¹ = 0.9375

يمكننا حساب كل احتمال تراكمي باستخدام صيغة مماثلة:

P(X≥0) = 1 – (1-.5) ⁰⁺¹ = 0.5

ف (X ≥1) = 1 – (1-0.5) ¹⁺¹ = 0.75

ف(X≥2) = 1 – (1-0.5) ²⁺¹ = 0.875

يمكننا حساب هذه الاحتمالات التراكمية لأي عدد من رميات العملة حتى ما لا نهاية. يمكننا بعد ذلك إنشاء رسم بياني لتصور هذا التوزيع الاحتمالي التراكمي:

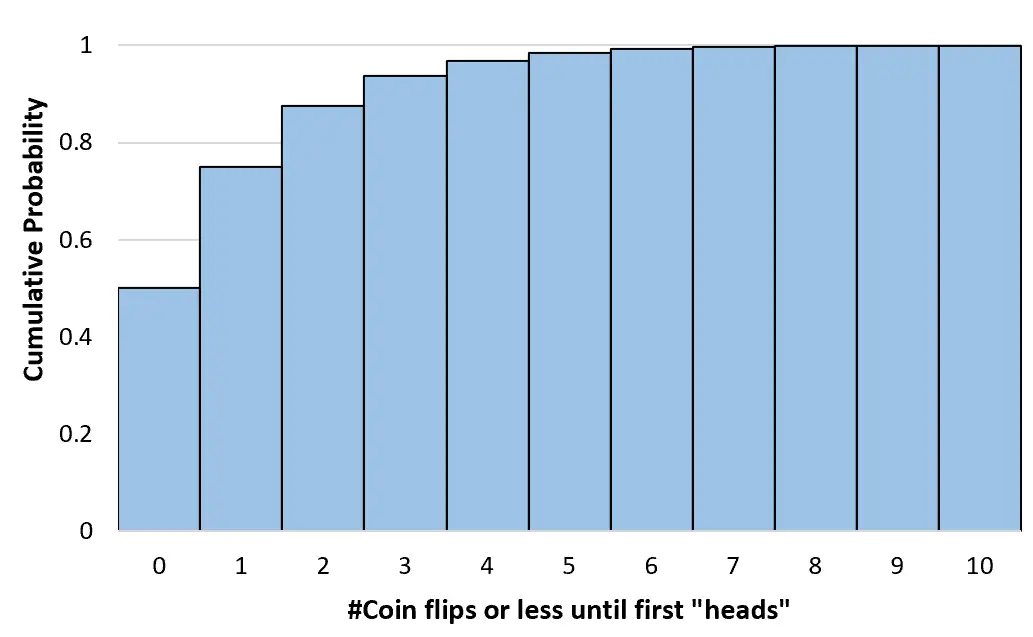
خصائص التوزيع الهندسي

التوزيع الهندسي له الخصائص التالية:

متوسط التوزيع هو (1-ع) / ع .

تباين التوزيع هو (1-ع) / ع ² .

على سبيل المثال:

متوسط عدد المرات التي نتوقع فيها أن تهبط العملة على الصورة قبل أن تهبط الكتابة على الصورة هو (1-p) / p = (1-.5) / .5 = 1 .

سيكون تباين عدد الرميات حتى يهبط على الرؤوس هو (1-p)/ ^p2 =(1-.5)/. ⁵² = 2 .

مشاكل ممارسة التوزيع الهندسي

استخدم المسائل التدريبية التالية لاختبار معرفتك بالتوزيع الهندسي.

ملحوظة: سوف نستخدم حاسبة التوزيع الهندسي لحساب إجابات هذه الأسئلة.

المشكلة 1

سؤال: ينتظر أحد الباحثين خارج المكتبة ليسأل الناس عما إذا كانوا يؤيدون قانونًا معينًا. احتمال أن يدعم شخص ما القانون هو p = 0.2. ما احتمال أن يكون الشخص الرابع الذي يتحدث إليه الباحث هو أول من يؤيد القانون؟

الجواب: عدد “الفاشلين” حتى النجاح الأول – أي عدد الأشخاص الذين لا يؤيدون القانون حتى يؤيده الشخص الأول – هو 3. لذا، في استخدام حاسبة التوزيع الهندسي حيث p = 0.2 وx = 3 حالات فشل نجد أن P(X=3) = 0.10240 .

المشكلة 2

سؤال: ينتظر أحد الباحثين خارج المكتبة ليسأل الناس عما إذا كانوا يؤيدون قانونًا معينًا. احتمال أن يدعم شخص ما القانون هو p = 0.2. ما هو احتمال أن يتحدث الباحث مع أكثر من أربعة أشخاص للعثور على شخص يؤيد القانون؟

الإجابة: باستخدام حاسبة التوزيع الهندسي مع فشل p =0.2 و x = 4، نجد أن P(X>4) = 0.32768 .

المشكلة 3

سؤال: ينتظر أحد الباحثين خارج المكتبة ليسأل الناس عما إذا كانوا يؤيدون قانونًا معينًا. احتمال أن يدعم شخص ما القانون هو p = 0.2. ما هو العدد المتوقع للأشخاص الذين ستحتاج الباحثة إلى التحدث معهم حتى تجد من يؤيد القانون؟

الإجابة: تذكر أن متوسط التوزيع الهندسي هو (1-p) /p . في هذه الحالة، سيكون المتوسط (1-.2) / .2 = 4 .