مقدمة للتوزيع متعدد الحدود

يصف التوزيع متعدد الحدود احتمال الحصول على عدد محدد من التعدادات لنتائج مختلفة ، عندما يكون لكل نتيجة احتمال ثابت لحدوثها.

_إذا كان من الممكن العثور على متغير _عشوائي _ _{بالصيغة} التالية:

الاحتمال = ن! * (ع ₁ ^{× ₁} * ع ₂ ^{× ₂} * … * ع _ك ^{س _ك} ) / (س ₁ ! * س ₂ ! … * س _ك !)

ذهب:

• ن: العدد الإجمالي للأحداث
• × ₁ : عدد مرات ظهور النتيجة 1
• p ₁ : احتمال حدوث النتيجة 1 في تجربة معينة

على سبيل المثال، لنفترض أن هناك 5 كرات حمراء، و3 كرات خضراء، و2 كرات زرقاء في جرة. إذا سحبنا 5 كرات عشوائيًا من الجرة، مع الاستبدال، ما هو احتمال الحصول على كرتين أحمرتين بالضبط، وكرتين أخضرتين، ورخام واحدة زرقاء؟

للإجابة على هذا السؤال، يمكننا استخدام التوزيع متعدد الحدود مع المعلمات التالية:

• ن : 5
• × ₁ (# كرات حمراء) = 2، × ₂ (# كرات خضراء) = 2، × ₃ (# كرات زرقاء) = 1
• ع ₁ (احتمال أحمر) = 0.5، ع ₂ (احتمال أخضر) = 0.3، ع ₃ (احتمال أزرق) = 0.2

وبالتعويض بهذه الأرقام في الصيغة نجد أن الاحتمال هو:

الاحتمال = 5! * (.5 ² * .3 ² * .2 ¹ ) / (2! * 2! * 1!) = 0.135 .

مشاكل ممارسة التوزيع متعدد الحدود

استخدم المسائل التدريبية التالية لاختبار معرفتك بالتوزيع متعدد الحدود.

ملحوظة: سوف نستخدم حاسبة التوزيع متعدد الحدود لحساب إجابات هذه الأسئلة.

المشكلة 1

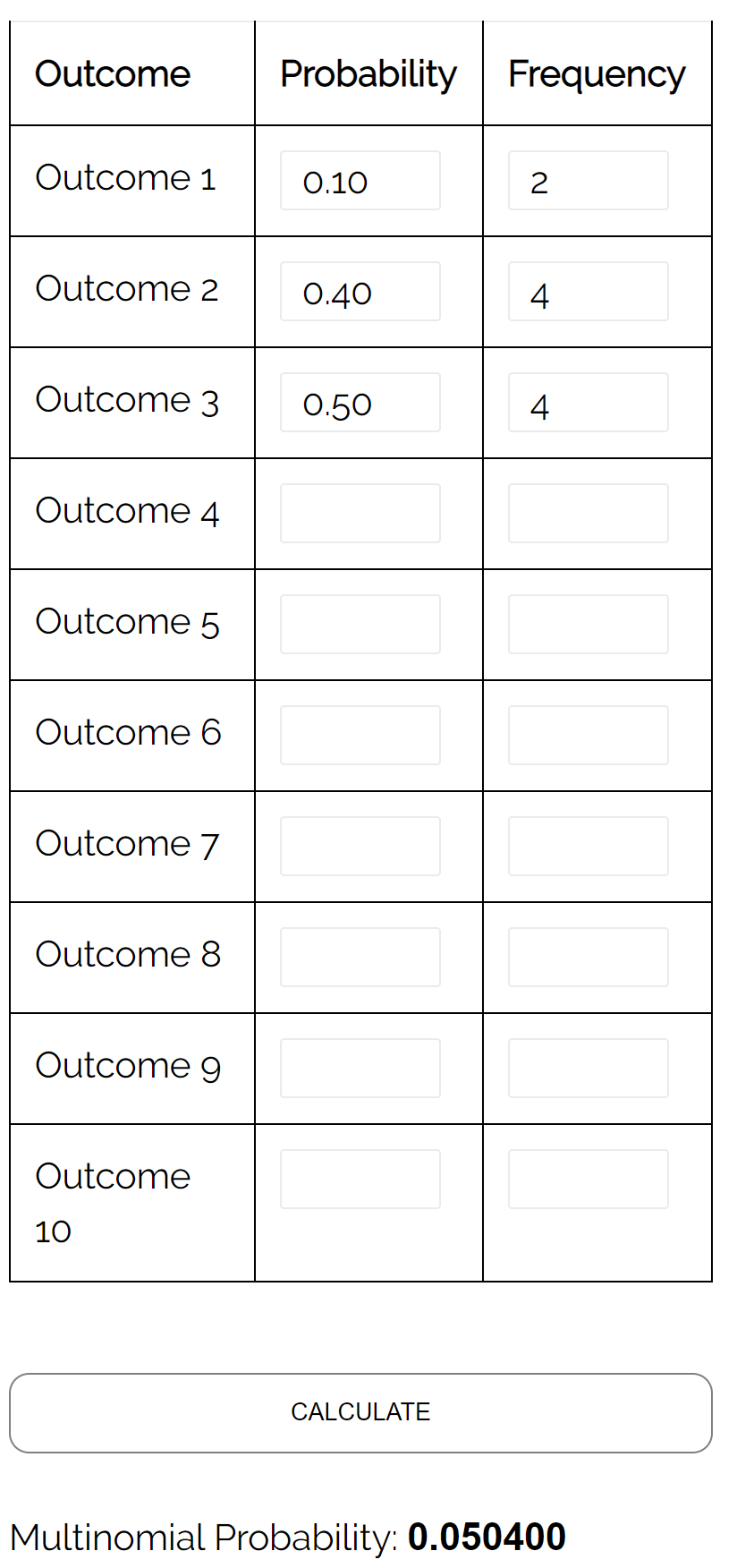
سؤال: في انتخابات ثلاثية لمنصب رئيس البلدية، يحصل المرشح “أ” على 10% من الأصوات، ويحصل المرشح “ب” على 40% من الأصوات، ويحصل المرشح “ج” على 50% من الأصوات. إذا اخترنا عينة عشوائية مكونة من 10 ناخبين، فما احتمال أن صوت 2 للمرشح أ، و4 صوت للمرشح ب، و4 صوتوا للمرشح ج؟

الإجابة: باستخدام حاسبة التوزيع متعدد الحدود مع المدخلات التالية، نجد أن الاحتمال هو 0.0504:

المشكلة 2

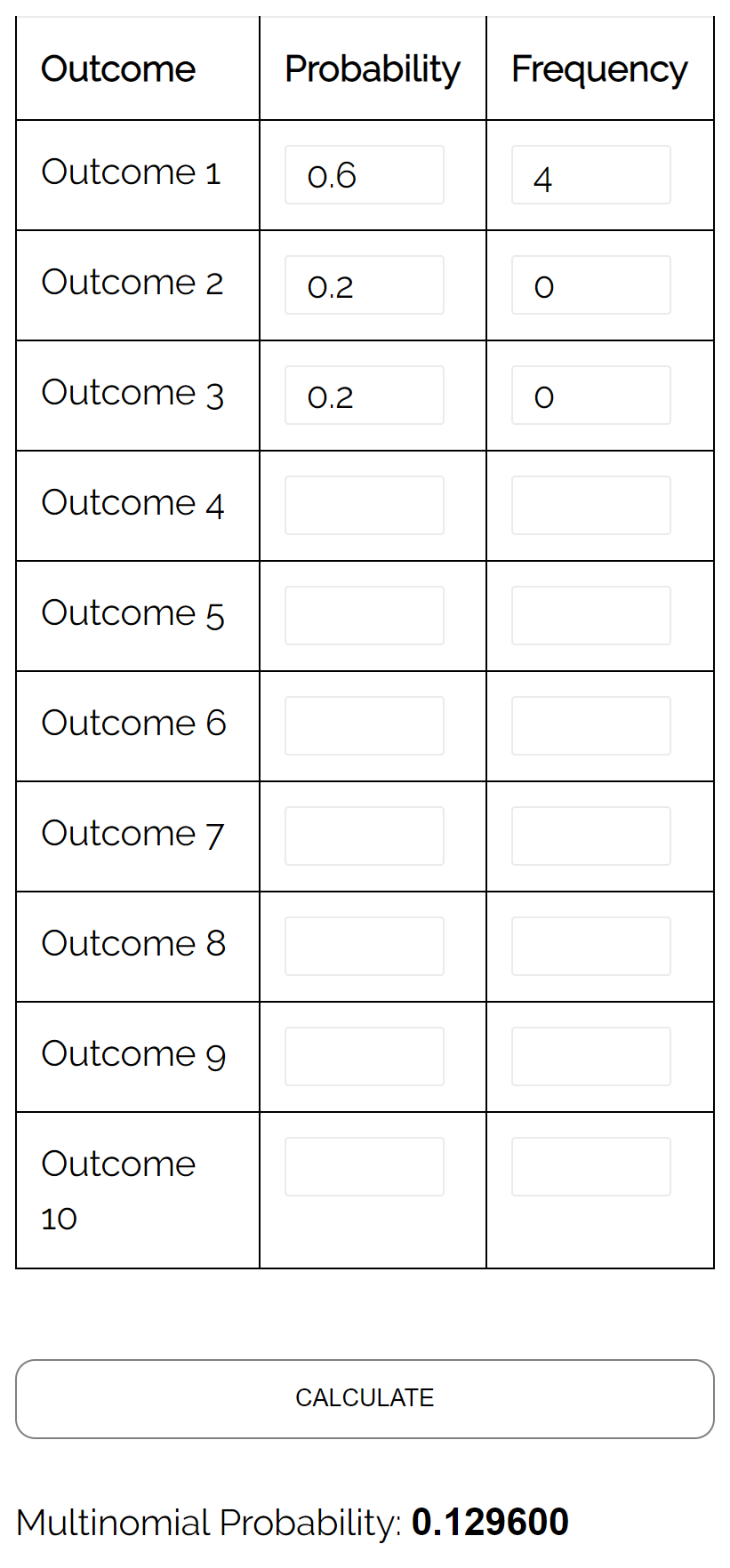
سؤال: افترض أن جرة تحتوي على 6 كرات صفراء، وكرتين أحمرتين، وكرتين ورديتين. إذا اخترنا أربع كرات عشوائيًا من الجرة، مع الاستبدال، فما احتمال أن تكون الكرات الأربع جميعها صفراء؟

الإجابة: باستخدام حاسبة التوزيع متعدد الحدود مع المدخلات التالية، نجد أن الاحتمال هو 0.1296:

المشكلة 3

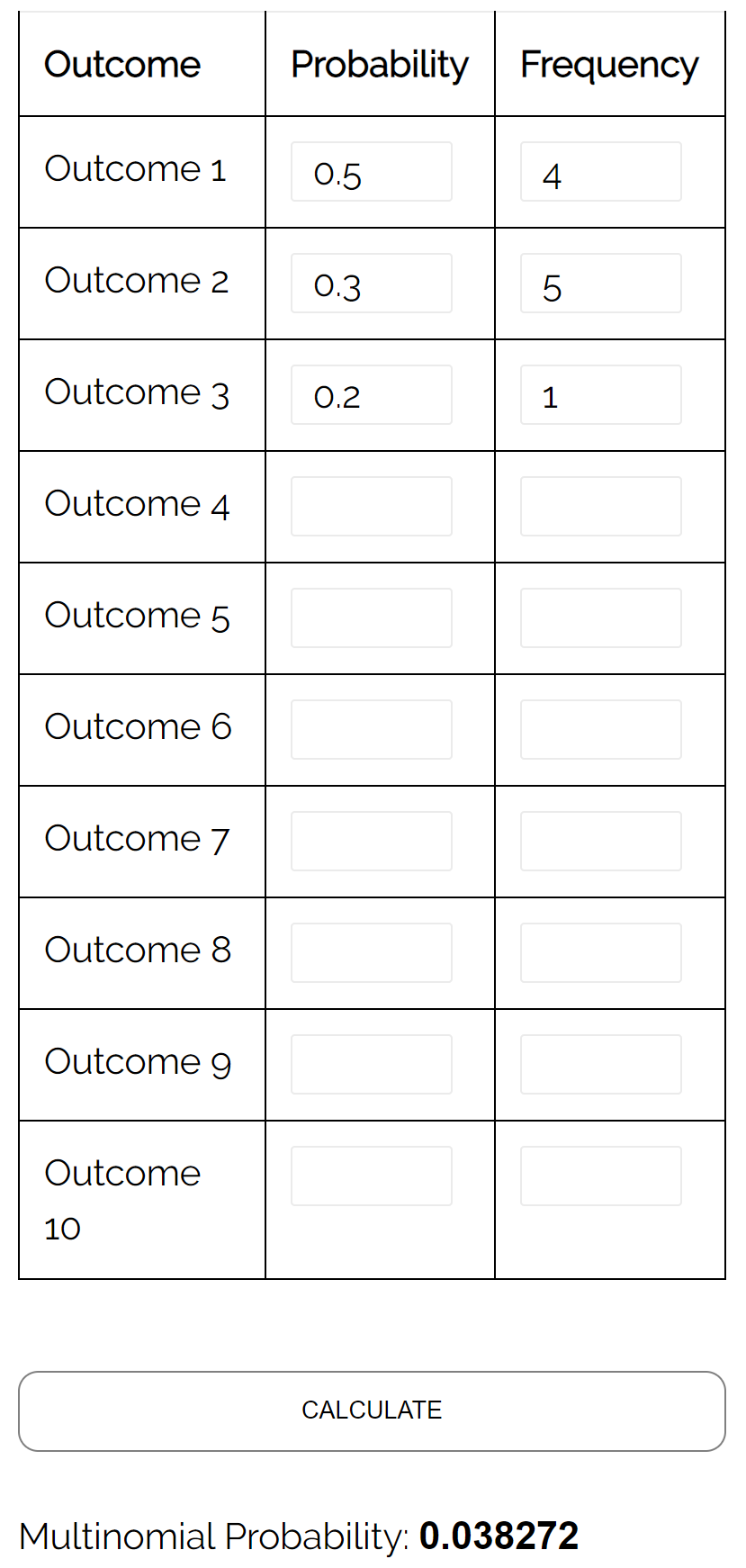
سؤال: لنفترض أن طالبين يلعبان الشطرنج ضد بعضهما البعض. احتمال فوز الطالب “أ” في لعبة معينة هو 0.5، واحتمال فوز الطالب “ب” في لعبة معينة هو 0.3، واحتمال وجود تعادل في لعبة معينة هو 0، 2. إذا لعبوا 10 ألعاب، فما هو احتمال أن يفوز اللاعب “أ” 4 مرات، ويفوز اللاعب “ب” 5 مرات، وأن يتعادلا مرة واحدة؟

الإجابة: باستخدام حاسبة التوزيع متعدد الحدود مع المدخلات التالية، نجد أن الاحتمال هو 0.038272:

مصادر إضافية

توفر البرامج التعليمية التالية مقدمة للتوزيعات الشائعة الأخرى في الإحصاء:

مقدمة للتوزيع الطبيعي
مقدمة للتوزيع ذي الحدين
مقدمة لتوزيع بواسون
مقدمة للتوزيع الهندسي