مصفوفة الارتباط

By دكتور بنيامين أندرسون زومار 5, 2023 إحصائيات 0 Comments

في هذه المقالة سوف تكتشف ما هي مصفوفة الارتباط، وما هي صيغتها وكيفية تفسير مصفوفة الارتباط. بالإضافة إلى ذلك، سوف تكون قادرًا على رؤية مثال ملموس لتفسير مصفوفة الارتباط.

ما هي مصفوفة الارتباط؟

مصفوفة الارتباط هي مصفوفة تحتوي في الموضع i,j على معامل الارتباط بين المتغيرين i و j .

لذلك فإن مصفوفة الارتباط هي مصفوفة مربعة مملوءة بأخرى على القطر الرئيسي ويتكون عنصر الصف i والعمود j من قيمة معامل الارتباط بين المتغير i والمتغير j .

وبالتالي فإن صيغة مصفوفة الارتباط هي كما يلي:

ذهب

$r_{ij}$

هو معامل الارتباط بين المتغيرات

$i$

$j.$

لذلك، من أجل العثور على مصفوفة الارتباط لمجموعة بيانات، من الضروري أن تعرف كيفية حساب معامل الارتباط. في حالة عدم تذكرك، ستجد في الرابط التالي كيفية القيام بذلك باستخدام الآلة الحاسبة عبر الإنترنت:

➤ انظر: حاسبة معامل الارتباط

ومن خصائص معامل الارتباط أن ترتيب المتغيرات لا يهم في حسابه، أي معامل الارتباط

$r_{ij}$

يعادل

$r_{ji}.$

ولذلك، فإن مصفوفة الارتباط متماثلة.

$\displaystyle R=\begin{pmatrix}1&r_{12}&r_{13}&\dots&r_{1n}\\[1.1ex] r_{12}&1&r_{23}&\dots&r_{2n}\\[1.1ex] r_{13}&r_{23}&1&\dots&r_{3n}\\[1.1ex] \vdots &\vdots &\vdots &\ddots &\vdots\\[1.1ex] r_{1n}&r_{2n}&r_{3n}&\dots&1\end{pmatrix}$

لكي تكون مصفوفة الارتباط ذات معنى، يجب أن تحتوي مجموعة البيانات الإحصائية على أكثر من متغيرين. وبخلاف ذلك، سيكون كافيا تحديد معامل ارتباط واحد وستكون مصفوفة الارتباط ذات معنى.

كيفية عمل مصفوفة الارتباط

بالنظر إلى تعريف مصفوفة الارتباط، دعونا نرى كيف يتم إنشاء هذا النوع من المصفوفات الإحصائية:

احسب معامل الارتباط لكل زوج من المتغيرات. لاحظ أن ترتيب المتغيرات لا يغير النتيجة، لذلك يجب حسابه مرة واحدة فقط لكل زوج من المتغيرات.
قم بإنشاء مصفوفة مربعة لها نفس البعد مثل عدد المتغيرات في سلسلة البيانات. ستكون هذه المصفوفة هي مصفوفة الارتباط.
ضع 1 في كل عنصر من عناصر القطر الرئيسي لمصفوفة الارتباط.
ضع معامل الارتباط للمتغيرات i , j في المواضع i , j و j , i .
بمجرد إنشاء مصفوفة الارتباط، كل ما تبقى هو تفسير قيمها.

ضع في اعتبارك أن مجرد تشغيل مصفوفة الارتباط لا يكفي، فأنت بحاجة بعد ذلك إلى تفسير قيمها وفهم ما تعنيه. يشرح القسم التالي كيفية تفسير مصفوفة الارتباط.

تفسير مصفوفة الارتباط

لتفسير مصفوفة الارتباط بشكل صحيح، من الضروري أن نأخذ في الاعتبار أن قيمة معامل الارتباط يمكن أن تتراوح من -1 إلى +1:

r=-1 : المتغيران لهما علاقة سلبية تامة، حتى نتمكن من رسم خط ذو ميل سلبي ترتبط فيه جميع النقاط.
-1<r<0 : الارتباط بين المتغيرين سلبي، فإذا زاد أحد المتغيرين انخفض الآخر. كلما كانت القيمة أقرب إلى -1، كلما كانت العلاقة بين المتغيرات أكثر سلبية.
r=0 : الارتباط بين المتغيرين ضعيف جداً، في الواقع العلاقة الخطية بينهما صفر. وهذا لا يعني أن المتغيرات مستقلة، إذ يمكن أن تكون لها علاقة غير خطية.
0<r<1 : تكون العلاقة بين المتغيرين موجبة، وكلما اقتربت القيمة من +1، كانت العلاقة بين المتغيرين أقوى. في هذه الحالة، يميل أحد المتغيرات إلى زيادة قيمته عندما يزيد الآخر أيضًا.
r=1 : المتغيران لهما علاقة إيجابية تامة، أي أن لديهما علاقة خطية موجبة.

وبالتالي، لتفسير مصفوفة الارتباط، من الضروري تفسير كل معامل ارتباط ومقارنة النتائج المختلفة.

بهذه الطريقة سوف تكون قادرًا على معرفة أي المتغيرات أكثر ارتباطًا ببعضها البعض، وأي المتغيرات هي الأكثر أهمية، وأي المتغيرات ليس لها أي علاقة عمليًا مع بعضها البعض، وما إلى ذلك.

مثال مصفوفة الارتباط

لفهم مكونات مصفوفة الارتباط بشكل كامل وكيفية تفسيرها، سنقوم في هذا القسم بتحليل مثال لمصفوفة الارتباط:

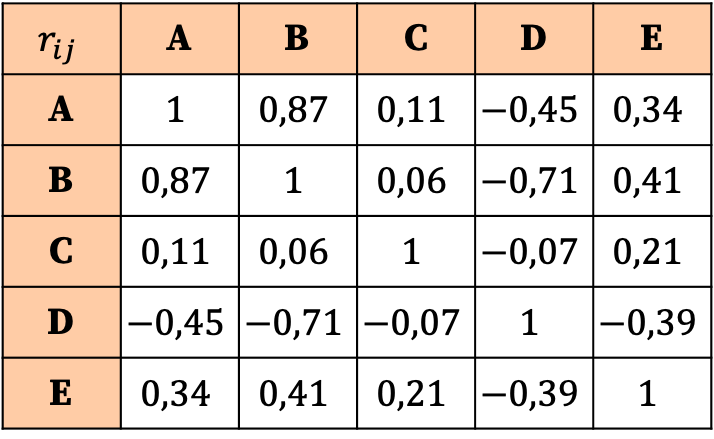
يعتمد تفسير مصفوفة الارتباط على قيم المعاملات. وهكذا يمكننا أن نرى أن أقوى ارتباط هو العلاقة بين المتغير A والمتغير B، حيث أن المعامل المقابل له هو الأكبر (0.87).

من ناحية أخرى، فإن المتغير C ليس له أي ارتباط عمليًا بأي متغير، نظرًا لأن جميع معاملاته قريبة جدًا من الصفر وبالتالي منخفضة جدًا. وبالتالي، لتبسيط التحليل، يمكننا أيضًا التفكير في إزالة هذا المتغير من الدراسة الإحصائية.

وبالمثل، فإن جميع علاقات المتغير D مع المتغيرات الأخرى تكون سلبية، مما يعني أن العلاقة بين المتغير D والمتغيرات الأخرى تكون عكسية. وهذا لا يعني أنه ينبغي حذف المتغير، بل يعني فقط أن المتغير D يرتبط ارتباطًا سلبيًا.

كما ترون، فإن مصفوفة الارتباط مفيدة جدًا لتلخيص البيانات وإجراء تحليل شامل للعلاقة بين المتغيرات المختلفة في مجموعة البيانات.

About Author

دكتور بنيامين أندرسون

مرحبًا، أنا بنجامين، أستاذ الإحصاء المتقاعد الذي تحول إلى مدرس متخصص في Statorials. بفضل خبرتي الواسعة في مجال الإحصاء، فأنا حريص على مشاركة معرفتي لتمكين الطلاب من خلال Statorials. تعرف أكثر