كيفية حساب dfbetas في r

في الإحصاء، غالبًا ما نرغب في معرفة تأثير الملاحظات المختلفة في نماذج الانحدار.

تتمثل إحدى طرق حساب تأثير الملاحظات في استخدام مقياس يُعرف باسم DFBETAS ، والذي يخبرنا بالتأثير المعياري على كل معامل لإزالة كل ملاحظة على حدة.

يمنحنا هذا المقياس فكرة عن تأثير كل ملاحظة على كل تقدير للمعامل في نموذج انحدار معين.

يعرض هذا البرنامج التعليمي مثالًا خطوة بخطوة لكيفية حساب وتصور DFBETAS لكل ملاحظة في نموذج في R.

الخطوة 1: إنشاء نموذج الانحدار

أولاً، سنقوم بإنشاء نموذج انحدار خطي متعدد باستخدام مجموعة بيانات mtcars المضمنة في R:

 #fit a regression model
model <- lm(mpg~disp+hp, data=mtcars)

#view model summary
summary(model)

Coefficients:
             Estimate Std. Error t value Pr(>|t|)    
(Intercept) 30.735904 1.331566 23.083 < 2nd-16 ***
available -0.030346 0.007405 -4.098 0.000306 ***
hp -0.024840 0.013385 -1.856 0.073679 .  
---
Significant. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Residual standard error: 3.127 on 29 degrees of freedom
Multiple R-squared: 0.7482, Adjusted R-squared: 0.7309 
F-statistic: 43.09 on 2 and 29 DF, p-value: 2.062e-09

الخطوة 2: حساب DFBETAS لكل ملاحظة

بعد ذلك، سوف نستخدم الدالة dfbetas() المضمنة لحساب قيم DFBETAS لكل ملاحظة في النموذج:

 #calculate DFBETAS for each observation in the model
dfbetas <- as . data . frame (dfbetas(model))

#display DFBETAS for each observation
dfbetas

                      (Intercept) disp hp
Mazda RX4 -0.1174171253 0.030760632 1.748143e-02
Mazda RX4 Wag -0.1174171253 0.030760632 1.748143e-02
Datsun 710 -0.1694989349 0.086630144 -3.332781e-05
Hornet 4 Drive 0.0577309674 0.078971334 -8.705488e-02
Hornet Sportabout -0.0204333878 0.237526523 -1.366155e-01
Valiant -0.1711908285 -0.139135639 1.829038e-01
Duster 360 -0.0312338677 -0.005356209 3.581378e-02
Merc 240D -0.0312259577 -0.010409922 2.433256e-02
Merc 230 -0.0865872595 0.016428917 2.287867e-02
Merc 280 -0.1560683502 0.078667906 -1.911180e-02
Merc 280C -0.2254489597 0.113639937 -2.760800e-02
Merc 450SE 0.0022844093 0.002966155 -2.855985e-02
Merc 450SL 0.0009062022 0.001176644 -1.132941e-02
Merc 450SLC 0.0041566755 0.005397169 -5.196706e-02
Cadillac Fleetwood 0.0388832216 -0.134511133 7.277283e-02
Lincoln Continental 0.0483781688 -0.121146607 5.326220e-02
Chrysler Imperial -0.1645266331 0.236634429 -3.917771e-02
Fiat 128 0.5720358325 -0.181104179 -1.265475e-01
Honda Civic 0.3490872162 -0.053660545 -1.326422e-01
Toyota Corolla 0.7367058819 -0.268512348 -1.342384e-01
Toyota Corona -0.2181110386 0.101336902 5.945352e-03
Dodge Challenger -0.0270169005 -0.123610713 9.441241e-02
AMC Javelin -0.0406785103 -0.141711468 1.074514e-01
Camaro Z28 0.0390139262 0.012846225 -5.031588e-02
Pontiac Firebird -0.0549059340 0.574544346 -3.689584e-01
Fiat X1-9 0.0565157245 -0.017751582 -1.262221e-02
Porsche 914-2 0.0839169111 -0.028670987 -1.240452e-02
Lotus Europa 0.3444562478 -0.402678927 2.135224e-01
Ford Pantera L -0.1598854695 -0.094184733 2.320845e-01
Ferrari Dino -0.0343997122 0.248642444 -2.344154e-01
Maserati Bora -0.3436265545 -0.511285637 7.319066e-01
Volvo 142E -0.1784974091 0.132692956 -4.433915e-02

لكل ملاحظة، يمكننا أن نرى الفرق في تقدير المعامل للأصل، ومتغير disp ، ومتغير hp الذي يحدث عندما نزيل تلك الملاحظة المحددة.

بشكل عام، نحن نعتبر أن الملاحظة لها تأثير قوي على تقدير معامل معين إذا كانت قيمة DBETAS أكبر من عتبة 2/√ n حيث n هو عدد الملاحظات.

في هذا المثال، ستكون العتبة 0.3535534 :

 #find number of observations
n <- nrow (mtcars)

#calculate DFBETAS threshold value
thresh <- 2/ sqrt (n)

thresh

[1] 0.3535534

الخطوة 3: تصور DFBETAS

أخيرًا، يمكننا إنشاء مخططات لتصور قيمة DFBETAS لكل ملاحظة ولكل متنبئ في النموذج:

 #specify 2 rows and 1 column in plotting region
by(mfrow=c(2,1))

#plot DFBETAS for disp with threshold lines
plot(dfbetas$disp, type=' h ')
abline(h = thresh, lty = 2)
abline(h = -thresh, lty = 2)

#plot DFBETAS for hp with threshold lines 
plot(dfbetas$hp, type=' h ')
abline(h = thresh, lty = 2)
abline(h = -thresh, lty = 2)

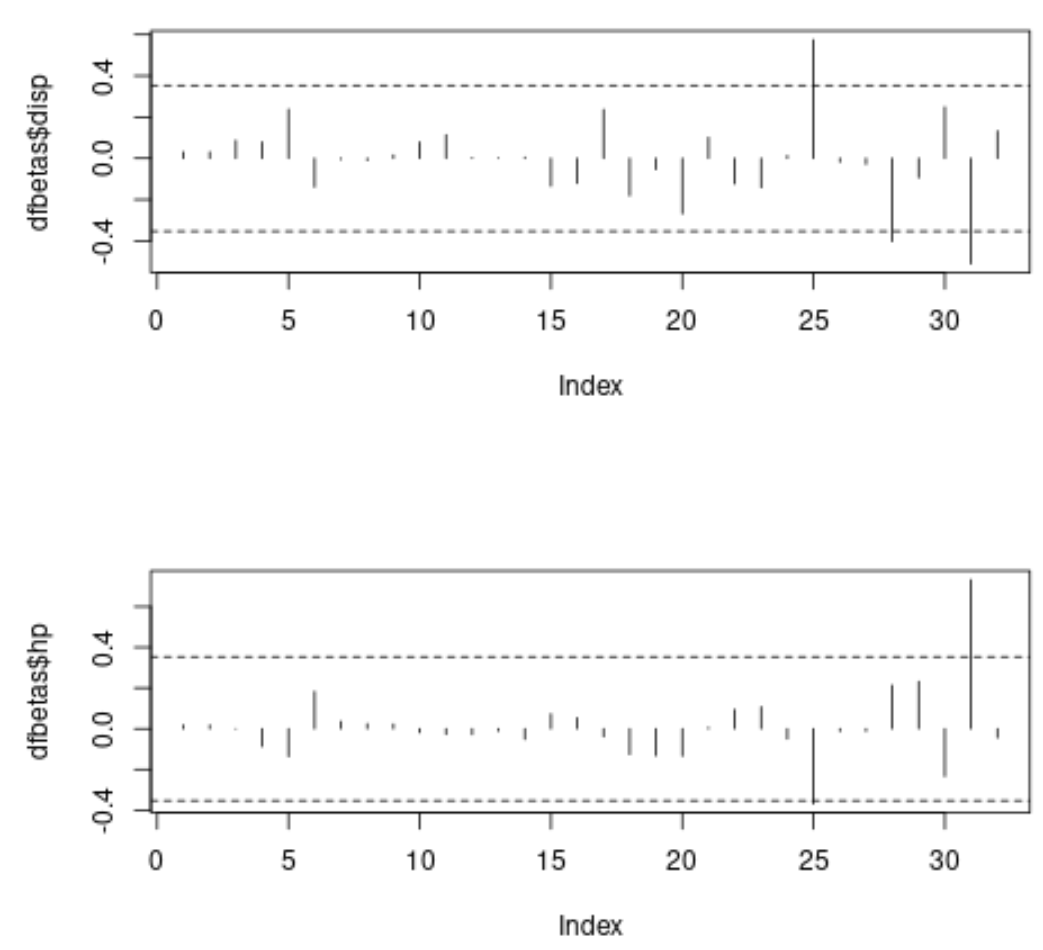
في كل مخطط، يعرض المحور x فهرس كل ملاحظة في مجموعة البيانات وتعرض القيمة y DFBETAS المقابلة لكل ملاحظة وكل متنبئ.

في المخطط الأول يمكننا أن نرى أن ثلاث ملاحظات تتجاوز قيمة العتبة المطلقة البالغة 0.3535534 وفي المخطط الثاني يمكننا أن نرى أن ملاحظتين تتجاوز قيمة العتبة المطلقة.

قد نختار دراسة هذه الملاحظات عن كثب لتحديد ما إذا كان لها تأثير غير ضروري على تقدير معاملات النموذج.

مصادر إضافية

كيفية إجراء الانحدار الخطي البسيط في R
كيفية إجراء الانحدار الخطي المتعدد في R
كيفية حساب إحصائيات الرافعة المالية في R
كيفية حساب DFFITS في R