K-يعني التجميع في r: مثال خطوة بخطوة

التجميع هو أسلوب للتعلم الآلي يحاول العثور على مجموعات من الملاحظات ضمن مجموعة بيانات.

الهدف هو العثور على مجموعات بحيث تكون الملاحظات داخل كل مجموعة متشابهة تمامًا مع بعضها البعض، في حين أن الملاحظات في مجموعات مختلفة تختلف تمامًا عن بعضها البعض.

التجميع هو شكل من أشكال التعلم غير الخاضع للرقابة لأننا نحاول ببساطة العثور على بنية ضمن مجموعة بيانات بدلاً من التنبؤ بقيمة متغير الاستجابة .

غالبًا ما يتم استخدام التجميع في التسويق عندما تتمكن الشركات من الوصول إلى معلومات مثل:

• دخل الأسرة
• حجم الأسرة
• مهنة رب الأسرة
• المسافة إلى أقرب منطقة حضرية

عندما تتوفر هذه المعلومات، يمكن استخدام التجميع لتحديد الأسر المتشابهة والتي قد تكون أكثر عرضة لشراء منتجات معينة أو الاستجابة بشكل أفضل لنوع معين من الإعلانات.

يُعرف أحد أكثر أشكال التجميع شيوعًا باسم التجميع بالوسائل k .

ما هو K-يعني التجميع؟

إن تجميع وسائل K هو أسلوب نضع فيه كل ملاحظة من مجموعة بيانات في إحدى مجموعات K.

الهدف النهائي هو الحصول على مجموعات K تكون فيها الملاحظات داخل كل مجموعة متشابهة تمامًا مع بعضها البعض بينما تختلف الملاحظات في المجموعات المختلفة تمامًا عن بعضها البعض.

من الناحية العملية، نستخدم الخطوات التالية لتنفيذ تجميع الوسائل K:

1. اختر قيمة لـ K.

• أولاً، نحتاج إلى تحديد عدد المجموعات التي نريد تحديدها في البيانات. غالبًا ما نحتاج ببساطة إلى اختبار عدة قيم مختلفة لـ K وتحليل النتائج لمعرفة عدد المجموعات التي يبدو أنها الأكثر منطقية لمشكلة معينة.

2. قم بتخصيص كل ملاحظة بشكل عشوائي لمجموعة أولية، من 1 إلى K.

3. قم بتنفيذ الإجراء التالي حتى تتوقف تعيينات المجموعة عن التغيير.

• لكل مجموعة من مجموعات K ، احسب مركز ثقل الكتلة. هذا هو ببساطة ناقل ميزات p- لملاحظات المجموعة k .
• تعيين كل ملاحظة إلى الكتلة مع أقرب النقطه الوسطى. هنا، يتم تعريف الأقرب باستخدام المسافة الإقليدية .

K-يعني التجميع في R

يوفر البرنامج التعليمي التالي مثالاً خطوة بخطوة لكيفية إجراء تجميع الوسائل k في R.

الخطوة 1: تحميل الحزم اللازمة

أولاً، سنقوم بتحميل حزمتين تحتويان على عدة وظائف مفيدة لتجميع الوسائل k في R.

 library (factoextra)
library (cluster)

الخطوة 2: تحميل البيانات وإعدادها

في هذا المثال، سنستخدم مجموعة بيانات USArrests المضمنة في R، والتي تحتوي على عدد الاعتقالات لكل 100000 شخص في كل ولاية أمريكية في عام 1973 بتهمة القتل والاعتداء والاغتصاب ، بالإضافة إلى النسبة المئوية لسكان كل ولاية الذين يعيشون في المناطق الحضرية المناطق. أوربان بوب .

يوضح الكود التالي كيفية القيام بما يلي:

• قم بتحميل مجموعة بيانات USArrests
• قم بإزالة كافة الصفوف ذات القيم المفقودة
• قم بقياس كل متغير في مجموعة البيانات للحصول على متوسط 0 وانحراف معياري 1

 #load data
df <-USArrests

#remove rows with missing values
df <- na. omitted (df)

#scale each variable to have a mean of 0 and sd of 1
df <- scale(df)

#view first six rows of dataset
head(df)

               Murder Assault UrbanPop Rape
Alabama 1.24256408 0.7828393 -0.5209066 -0.003416473
Alaska 0.50786248 1.1068225 -1.2117642 2.484202941
Arizona 0.07163341 1.4788032 0.9989801 1.042878388
Arkansas 0.23234938 0.2308680 -1.0735927 -0.184916602
California 0.27826823 1.2628144 1.7589234 2.067820292
Colorado 0.02571456 0.3988593 0.8608085 1.864967207

الخطوة 3: العثور على العدد الأمثل للمجموعات

لتنفيذ تجميع الوسائل k في R، يمكننا استخدام الدالة kmeans() المضمنة، والتي تستخدم الصيغة التالية:

kmeans (البيانات، المراكز، nstart)

ذهب:

• البيانات: اسم مجموعة البيانات.
• المراكز: عدد التجمعات، المشار إليها ك .
• nstart: عدد التكوينات الأولية. نظرًا لأنه من الممكن أن تؤدي مجموعات البداية المختلفة إلى نتائج مختلفة، فمن المستحسن استخدام عدة تكوينات أولية مختلفة. سوف تجد خوارزمية k-means التكوينات الأولية التي تؤدي إلى أصغر اختلاف داخل المجموعة.

نظرًا لأننا لا نعرف مسبقًا عدد المجموعات الأمثل، فسنقوم بإنشاء رسمين بيانيين مختلفين يمكن أن يساعدونا في اتخاذ القرار:

1. عدد المجموعات نسبة إلى المجموع في مجموع المربعات

أولاً، سنستخدم الدالة fviz_nbclust() لإنشاء رسم بياني لعدد العناقيد مقابل الإجمالي في مجموع المربعات:

 fviz_nbclust(df, kmeans, method = “ wss ”) 

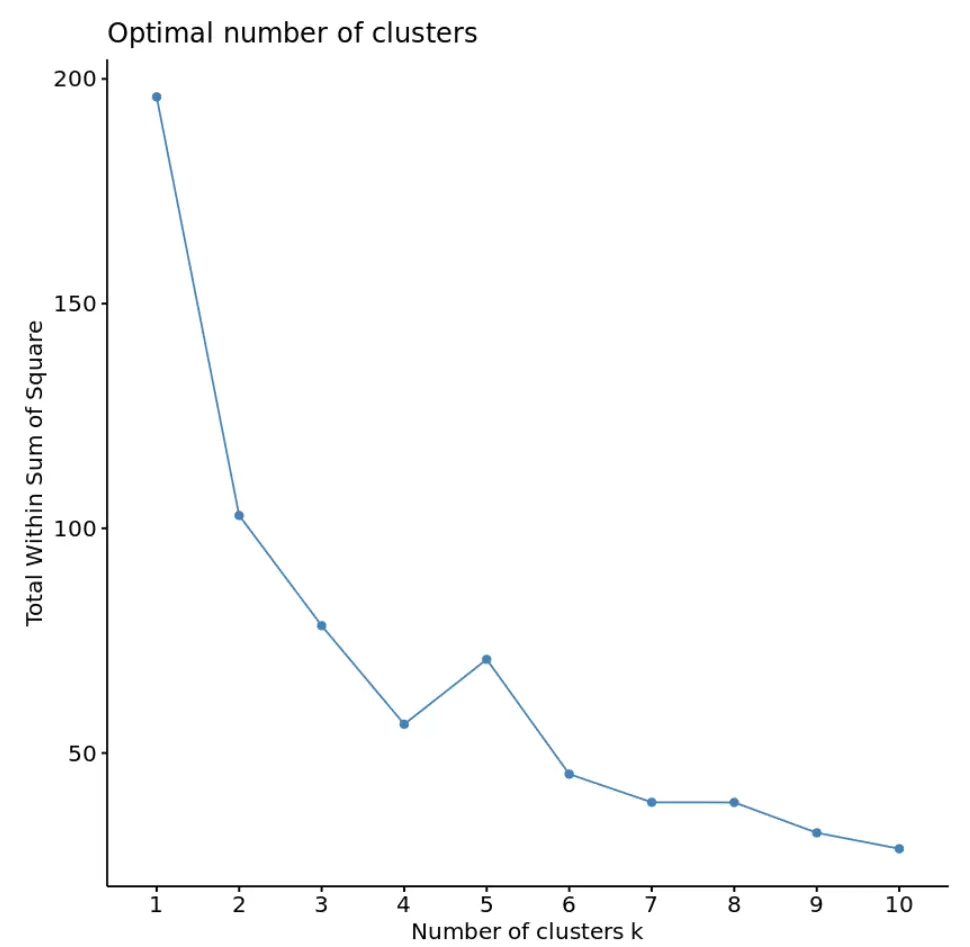
عادة، عندما نقوم بإنشاء هذا النوع من الحبكة، فإننا نبحث عن “الركبة” حيث يبدأ مجموع المربعات في “الانحناء” أو الاستقرار. هذا هو بشكل عام العدد الأمثل للمجموعات.

بالنسبة لهذا الرسم البياني، يبدو أن هناك انحناء صغير أو “انحناء” عند k = 4 مجموعات.

2. عدد المجموعات مقابل إحصاءات الفجوات

هناك طريقة أخرى لتحديد العدد الأمثل للمجموعات وهي استخدام مقياس يسمى إحصائية الانحراف ، والذي يقارن إجمالي التباين داخل المجموعة لقيم k المختلفة مع قيمها المتوقعة للتوزيع بدون تجميع.

يمكننا حساب إحصائية الفجوة لكل عدد من المجموعات باستخدام الدالة clusGap() من حزمة المجموعة وكذلك رسم المجموعات مقابل إحصائيات الفجوة باستخدام الدالة fviz_gap_stat() :

 #calculate gap statistic based on number of clusters
gap_stat <- clusGap(df,
                    FUN = kmeans,
                    nstart = 25,
                    K.max = 10,
                    B = 50)

#plot number of clusters vs. gap statistic
fviz_gap_stat(gap_stat) 

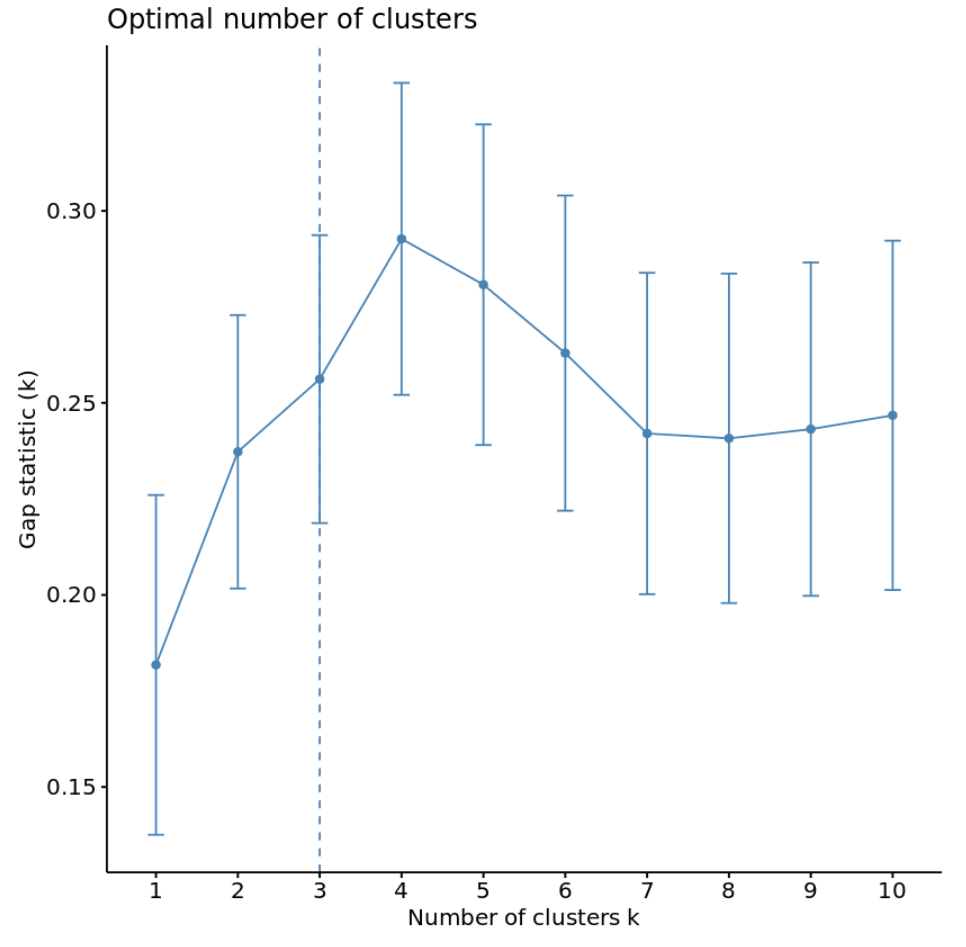
من الرسم البياني، يمكننا أن نرى أن إحصائية الفجوة هي الأعلى عند k = 4 مجموعات، وهو ما يتوافق مع طريقة الكوع التي استخدمناها سابقًا.

الخطوة 4: تنفيذ مجموعة K-Means باستخدام Optimal K

أخيرًا، يمكننا إجراء تجميع لوسائل k على مجموعة البيانات باستخدام القيمة المثالية لـ k لـ 4:

 #make this example reproducible
set.seed(1)

#perform k-means clustering with k = 4 clusters
km <- kmeans(df, centers = 4, nstart = 25)

#view results
km

K-means clustering with 4 clusters of sizes 16, 13, 13, 8

Cluster means:
      Murder Assault UrbanPop Rape
1 -0.4894375 -0.3826001 0.5758298 -0.26165379
2 -0.9615407 -1.1066010 -0.9301069 -0.96676331
3 0.6950701 1.0394414 0.7226370 1.27693964
4 1.4118898 0.8743346 -0.8145211 0.01927104

Vector clustering:
       Alabama Alaska Arizona Arkansas California Colorado 
             4 3 3 4 3 3 
   Connecticut Delaware Florida Georgia Hawaii Idaho 
             1 1 3 4 1 2 
      Illinois Indiana Iowa Kansas Kentucky Louisiana 
             3 1 2 1 2 4 
         Maine Maryland Massachusetts Michigan Minnesota Mississippi 
             2 3 1 3 2 4 
      Missouri Montana Nebraska Nevada New Hampshire New Jersey 
             3 2 2 3 2 1 
    New Mexico New York North Carolina North Dakota Ohio Oklahoma 
             3 3 4 2 1 1 
        Oregon Pennsylvania Rhode Island South Carolina South Dakota Tennessee 
             1 1 1 4 2 4 
         Texas Utah Vermont Virginia Washington West Virginia 
             3 1 2 1 1 2 
     Wisconsin Wyoming 
             2 1 

Within cluster sum of squares by cluster:
[1] 16.212213 11.952463 19.922437 8.316061
 (between_SS / total_SS = 71.2%)

Available components:

[1] "cluster" "centers" "totss" "withinss" "tot.withinss" "betweenss"   
[7] "size" "iter" "ifault"         

ومن النتائج يتبين لنا أن:

• تم تخصيص 16 ولاية للمجموعة الأولى
• وتم تخصيص 13 ولاية للمجموعة الثانية
• وتم تخصيص 13 ولاية للمجموعة الثالثة
• تم تخصيص 8 ولايات للمجموعة الرابعة

يمكننا تصور المجموعات على مخطط التشتت الذي يعرض أول مكونين رئيسيين على المحاور باستخدام الدالة fivz_cluster() :

 #plot results of final k-means model
fviz_cluster(km, data = df)

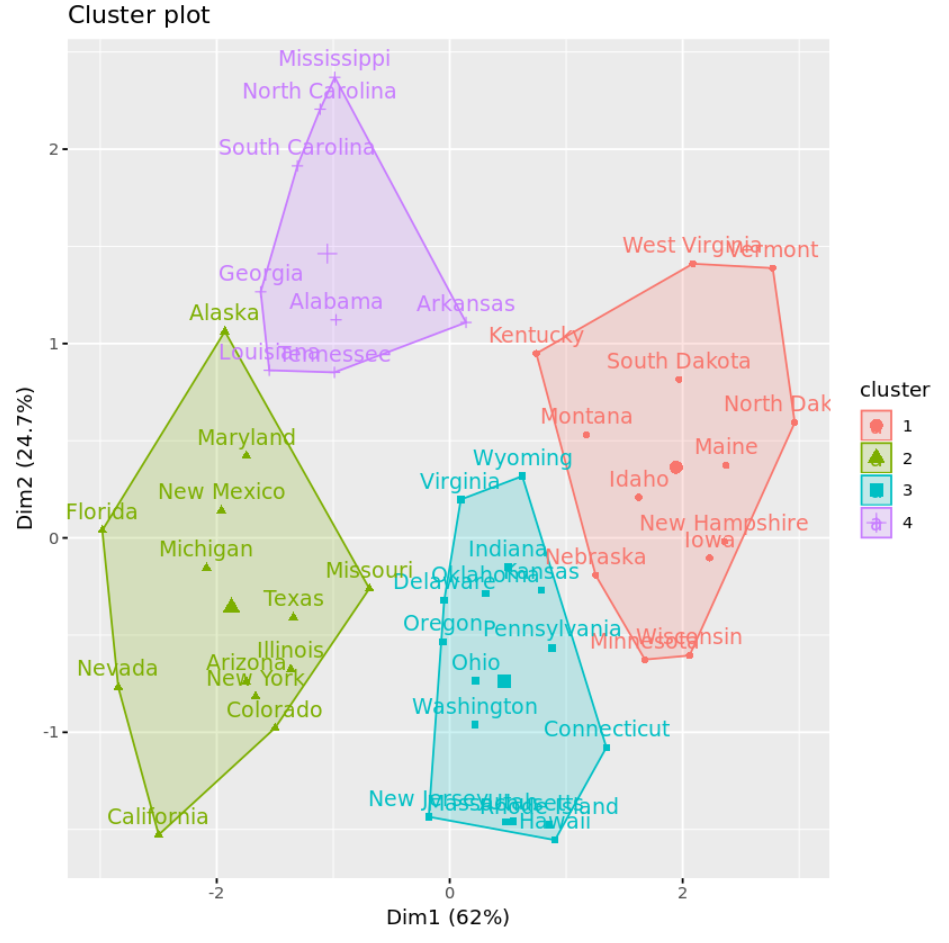
يمكننا أيضًا استخدام الدالة Aggregate() ‎ للعثور على متوسط المتغيرات في كل مجموعة:

 #find means of each cluster
aggregate(USArrests, by= list (cluster=km$cluster), mean)

cluster Murder Assault UrbanPop Rape
				
1 3.60000 78.53846 52.07692 12.17692
2 10.81538 257.38462 76.00000 33.19231
3 5.65625 138.87500 73.87500 18.78125
4 13.93750 243.62500 53.75000 21.41250

نحن نفسر هذا الإخراج على النحو التالي:

• ويبلغ متوسط عدد جرائم القتل لكل 100 ألف مواطن في دول المجموعة الأولى 3.6 .
• ويبلغ متوسط عدد الاعتداءات لكل 100 ألف مواطن بين دول المجموعة الأولى 78.5 .
• يبلغ متوسط النسبة المئوية للسكان الذين يعيشون في منطقة حضرية بين ولايات المجموعة الأولى 52.1% .
• متوسط عدد حالات الاغتصاب لكل 100.000 مواطن بين دول المجموعة الأولى هو 12.2 .

وما إلى ذلك وهلم جرا.

يمكننا أيضًا إضافة تخصيصات المجموعة لكل ولاية إلى مجموعة البيانات الأصلية:

 #add cluster assignment to original data
final_data <- cbind(USArrests, cluster = km$cluster)

#view final data
head(final_data)

	Murder Assault UrbanPop Rape cluster
				
Alabama 13.2 236 58 21.2 4
Alaska 10.0 263 48 44.5 2
Arizona 8.1 294 80 31.0 2
Arkansas 8.8 190 50 19.5 4
California 9.0 276 91 40.6 2
Colorado 7.9 204 78 38.7 2

مزايا وعيوب K-Means Clustering

يوفر تجميع الوسائل K المزايا التالية:

• إنها خوارزمية سريعة.
• يمكنه التعامل مع مجموعات البيانات الكبيرة بشكل جيد.

ومع ذلك، فإنه لديه العيوب المحتملة التالية:

• وهذا يتطلب منا تحديد عدد المجموعات قبل تشغيل الخوارزمية.
• إنها حساسة للقيم المتطرفة.

هناك بديلان للتجميع بالوسائل k هما التجميع بالوسائل k والتجمع الهرمي.

يمكنك العثور على رمز R الكامل المستخدم في هذا المثال هنا .