T-score و z-score: متى يتم استخدامها؟

المصطلحان اللذان غالبًا ما يربكان الطلاب في دورات الإحصاء هما T-scores و z-scores .

يُستخدم كلاهما على نطاق واسع عند إجراءاختبار الفرضيات أو إنشاء فترات الثقة ، لكنهما مختلفان قليلاً.

وهنا الصيغة لكل:

النتيجة ر = ( س – μ) / (ق/√ ن )

ذهب:

• x : وسائل العينة
• μ : متوسط عدد السكان
• s : عينة الانحراف المعياري
• ن : حجم العينة

النتيجة z = ( x – μ) / σ

ذهب:

• x : قيمة البيانات الأولية
• μ : متوسط عدد السكان
• σ : الانحراف المعياري للسكان

يوضح هذا المخطط الانسيابي متى يجب عليك استخدام كل منها، بناءً على بياناتك:

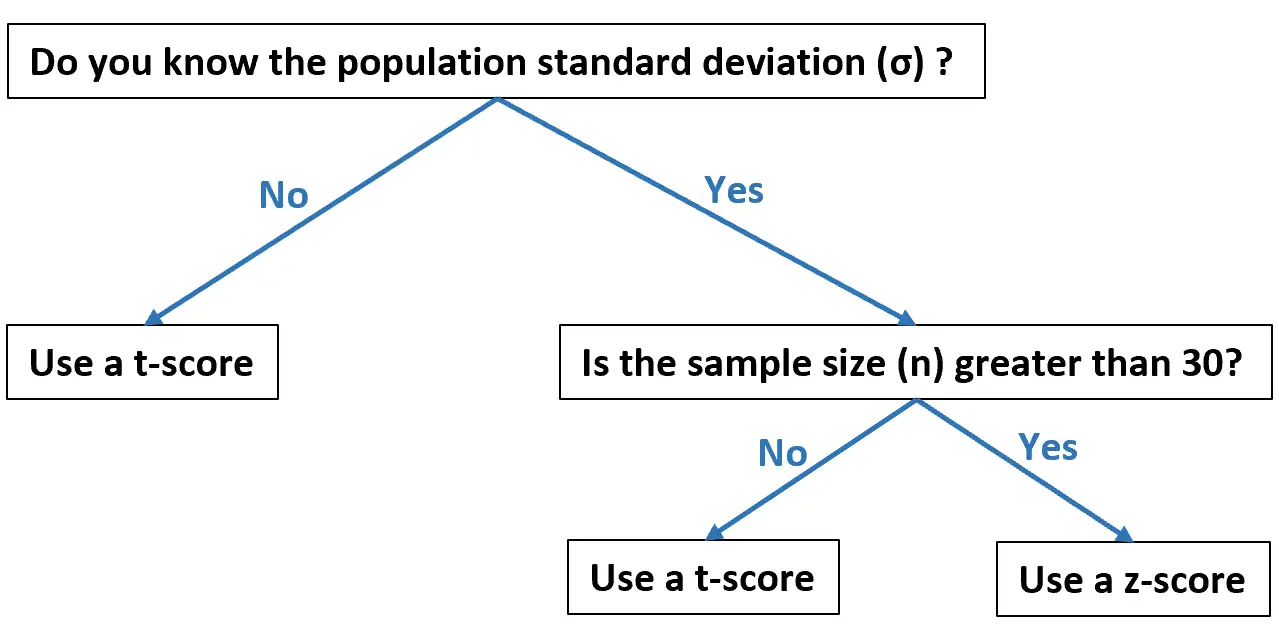
توضح الأمثلة التالية كيفية حساب درجة T ودرجة Z عمليًا.

مثال 1: حساب T-Score

لنفترض أن أحد المطاعم يقوم بإعداد الهامبرغر ويدعي أن متوسط وزنه هو μ = 0.25 رطل.

لنفترض أننا أخذنا عينة عشوائية من n = 20 همبرغر ووجدنا أن متوسط وزن العينة هو x = 0.22 رطل مع انحراف معياري قدره s = 0.05 رطل. قم بإجراء اختبار فرضي لتحديد ما إذا كان متوسط الوزن الفعلي لجميع أنواع الهامبرغر التي ينتجها هذا المطعم يساوي 0.25 رطل.

في هذا المثال، سوف نستخدم درجة T لإجراء اختبار الفرضية لأنه لم يتم استيفاء أي من الشرطين التاليين.

• الانحراف المعياري للسكان (σ) معروف. (لم يتم توفير σ في هذا المثال)
• حجم العينة أكبر من 30. (n=20 في هذا المثال)

لذلك، فإننا سوف نحسب درجة t على النحو التالي:

• النتيجة ر = ( س – μ) / (ق/√ ن )
• درجة t = (0.22 – 0.25) / (0.05 / √ 20 )
• درجة تي = -2.68

وفقًا لآلة حاسبة P-value T-score ، فإن القيمة p التي تتوافق مع درجة t هذه هي 0.01481 .

وبما أن هذه القيمة الاحتمالية أقل من 0.05، فلدينا أدلة كافية لنقول أن متوسط وزن الهامبرغر المنتج في هذا المطعم لا يساوي 0.25 رطل.

مثال 2: حساب درجة Z

افترض أن إحدى الشركات تقوم بتصنيع بطاريات من المعروف أن عمرها الافتراضي يتبع التوزيع الطبيعي بمتوسط μ = 20 ساعة وانحراف معياري قدره σ = 5 ساعات.

لنفترض أننا أخذنا عينة عشوائية من البطاريات n = 50 ووجدنا أن متوسط العينة هو x = 21 ساعة. قم بإجراء اختبار فرضي لتحديد ما إذا كان متوسط العمر الحقيقي لجميع البطاريات المصنعة من قبل هذه الشركة يساوي 20 ساعة.

في هذا المثال، سوف نستخدم درجة z لإجراء اختبار الفرضية لأنه يتم استيفاء الشرطين التاليين:

• الانحراف المعياري للسكان (σ) معروف. (σ تساوي 5 في هذا المثال)
• حجم العينة أكبر من 30. (n=50 في هذا المثال)

لذلك، فإننا سوف نحسب درجة z على النحو التالي:

• النتيجة z = ( x – μ) / σ
• النتيجة z = (21 – 20) / 5
• النتيجة z = 0.2

وفقًا لآلة حاسبة P-value Z-score، فإن القيمة p التي تتوافق مع Z-score هذه هي 0.84184 .

وبما أن هذه القيمة p لا تقل عن 0.05، فليس لدينا أدلة كافية لنقول إن متوسط عمر جميع البطاريات المصنعة من قبل هذه الشركة يختلف عن 20 ساعة.

مصادر إضافية

توفر البرامج التعليمية التالية مزيدًا من المعلومات حول نتائج T ونتائج Z:

التوزيع الطبيعي مقابل التوزيع t: ما الفرق؟
كيفية قراءة جدول التوزيع ر
كيفية قراءة الجدول Z