كيفية إجراء الانحدار التربيعي على الآلة الحاسبة ti-84

عندما يكون بين متغيرين علاقة خطية، يمكننا غالبًا استخدام الانحدار الخطي البسيط لتحديد العلاقة بينهما.

ومع ذلك، عندما يكون لمتغيرين علاقة تربيعية، يمكننا استخدام الانحدار التربيعي لتحديد العلاقة بينهما.

يشرح هذا البرنامج التعليمي كيفية إجراء الانحدار التربيعي على الآلة الحاسبة TI-84.

مثال: الانحدار التربيعي على الآلة الحاسبة TI-84

لنفترض أننا نريد أن نفهم العلاقة بين عدد ساعات العمل والسعادة. لدينا البيانات التالية عن عدد ساعات العمل أسبوعيًا ومستوى السعادة المُبلغ عنه (على مقياس من 0 إلى 100) لـ 11 شخصًا مختلفًا:

اتبع الخطوات التالية لإجراء الانحدار التربيعي على الآلة الحاسبة TI-84.

الخطوة 1: تصور البيانات.

قبل أن نتمكن من استخدام الانحدار التربيعي، يجب أن نتأكد من أن العلاقة بين المتغير التوضيحي (الساعات) ومتغير الاستجابة (السعادة) هي بالفعل علاقة تربيعية.

أولا سنقوم بإدخال قيم البيانات للمتغير التوضيحي ومتغير الاستجابة. اضغط على Stat ثم اضغط على EDIT . أدخل القيم التالية للمتغير التوضيحي (ساعات العمل) في العمود L1 والقيم الخاصة بمتغير الاستجابة (السعادة) في العمود L2:

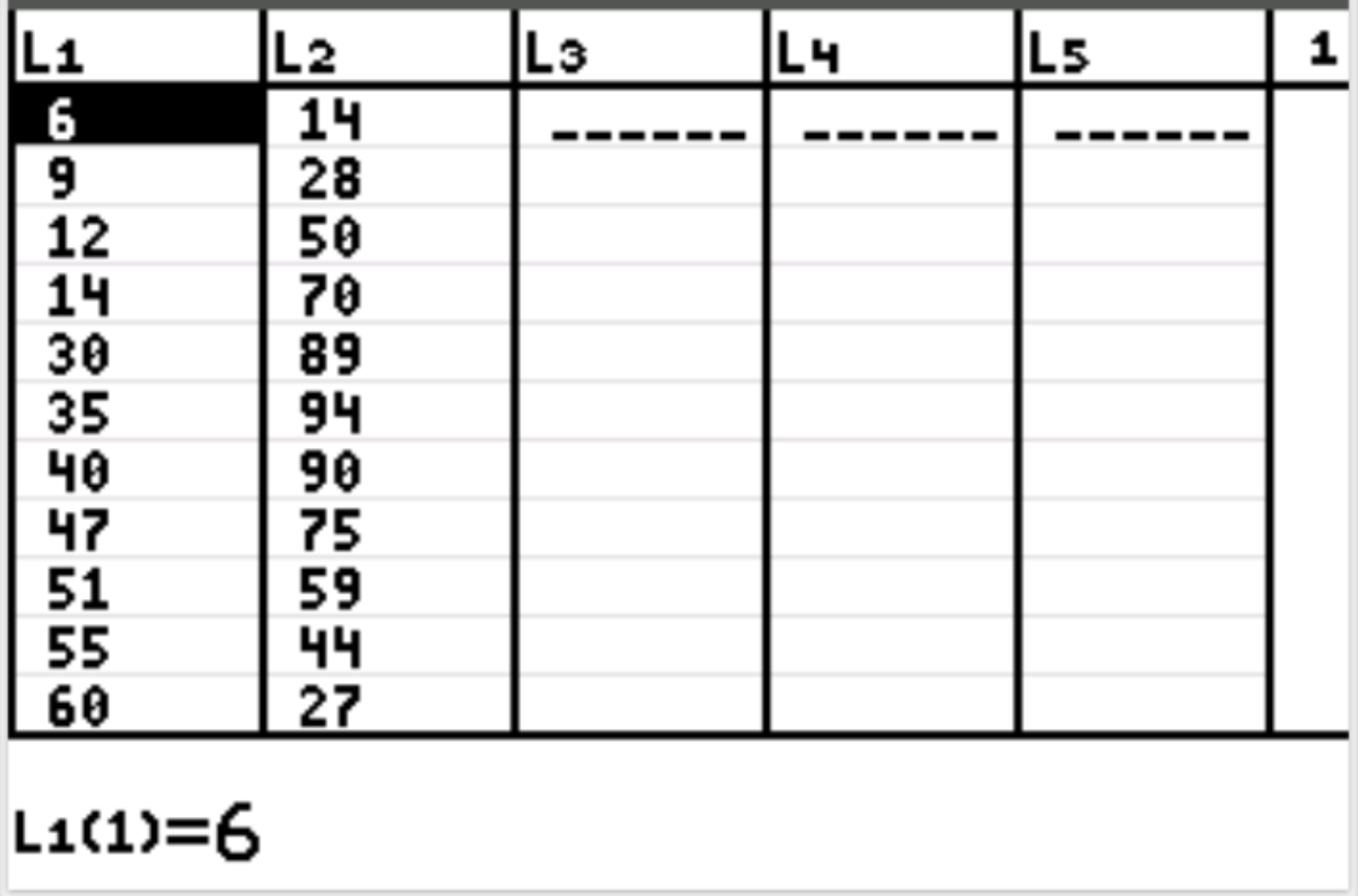
بعد ذلك، اضغط على 2nd ثم اضغط على y= للوصول إلى قائمة statplot . قم بتمييز Plot1 ثم اضغط على Enter . تأكد من تمكين التخطيط وتحديد L1 وL2 لـ Xlist وYlist على التوالي:

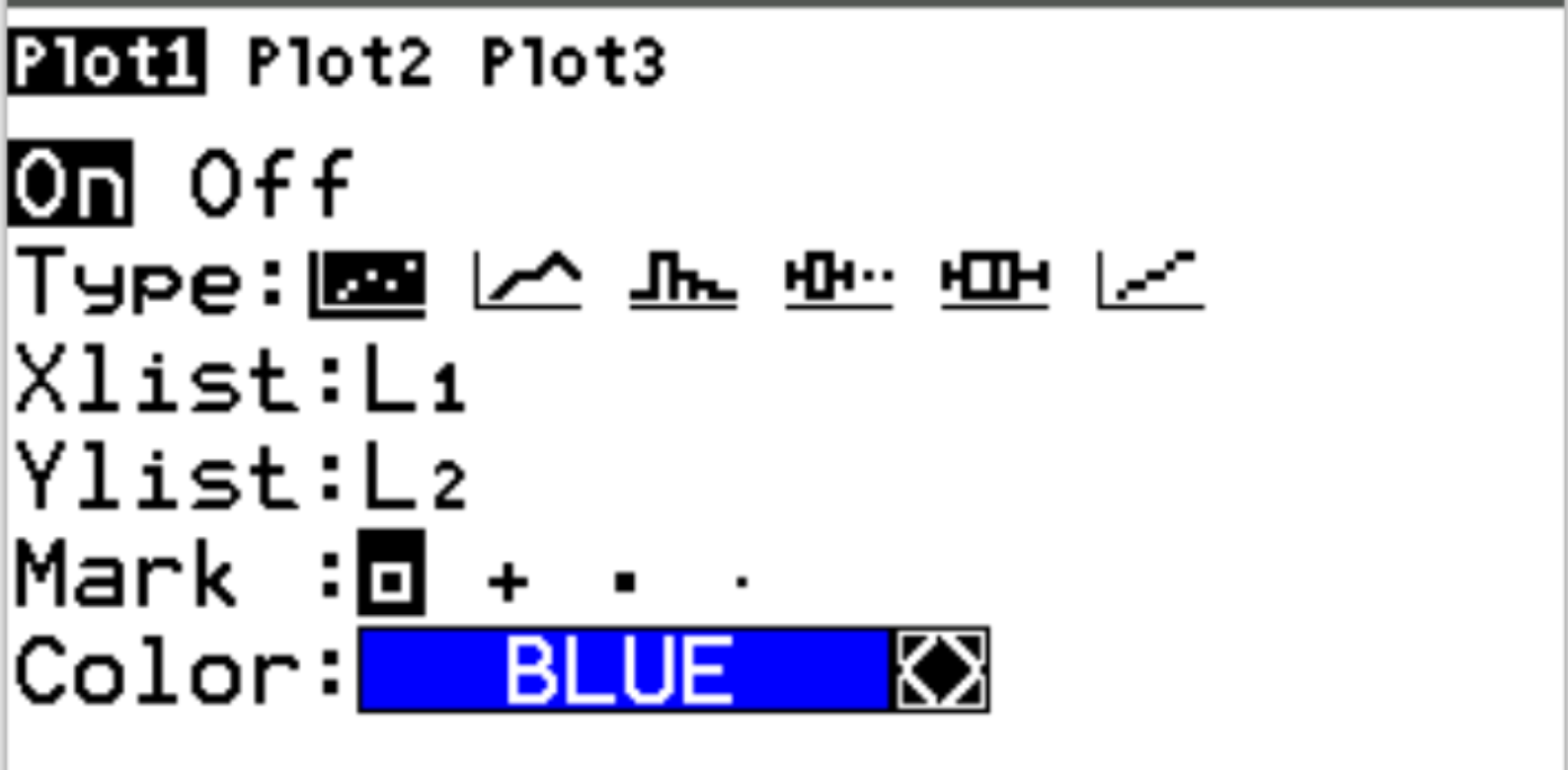
بعد ذلك، اضغط على Zoom ثم اضغط على 9:ZoomStat . سيؤدي هذا تلقائيًا إلى إنتاج السحابة النقطية التالية:

يمكننا أن نرى أن السعادة تميل إلى الزيادة مع زيادة عدد ساعات العمل من الصفر إلى نقطة معينة، ولكنها تبدأ بعد ذلك في الانخفاض مع زيادة عدد ساعات العمل بشكل أكبر.

يشير هذا الشكل المقلوب “U” في مخطط التشتت إلى وجود علاقة تربيعية بين ساعات العمل والسعادة، مما يعني أننا يجب أن نستخدم الانحدار التربيعي لتحديد هذه العلاقة.

الخطوة 2: تنفيذ الانحدار التربيعي.

بعد ذلك، سوف نقوم بإجراء الانحدار التربيعي. اضغط على Stat ثم قم بالتمرير إلى CALC . ثم قم بالتمرير إلى 5:QuadReg واضغط على Enter .

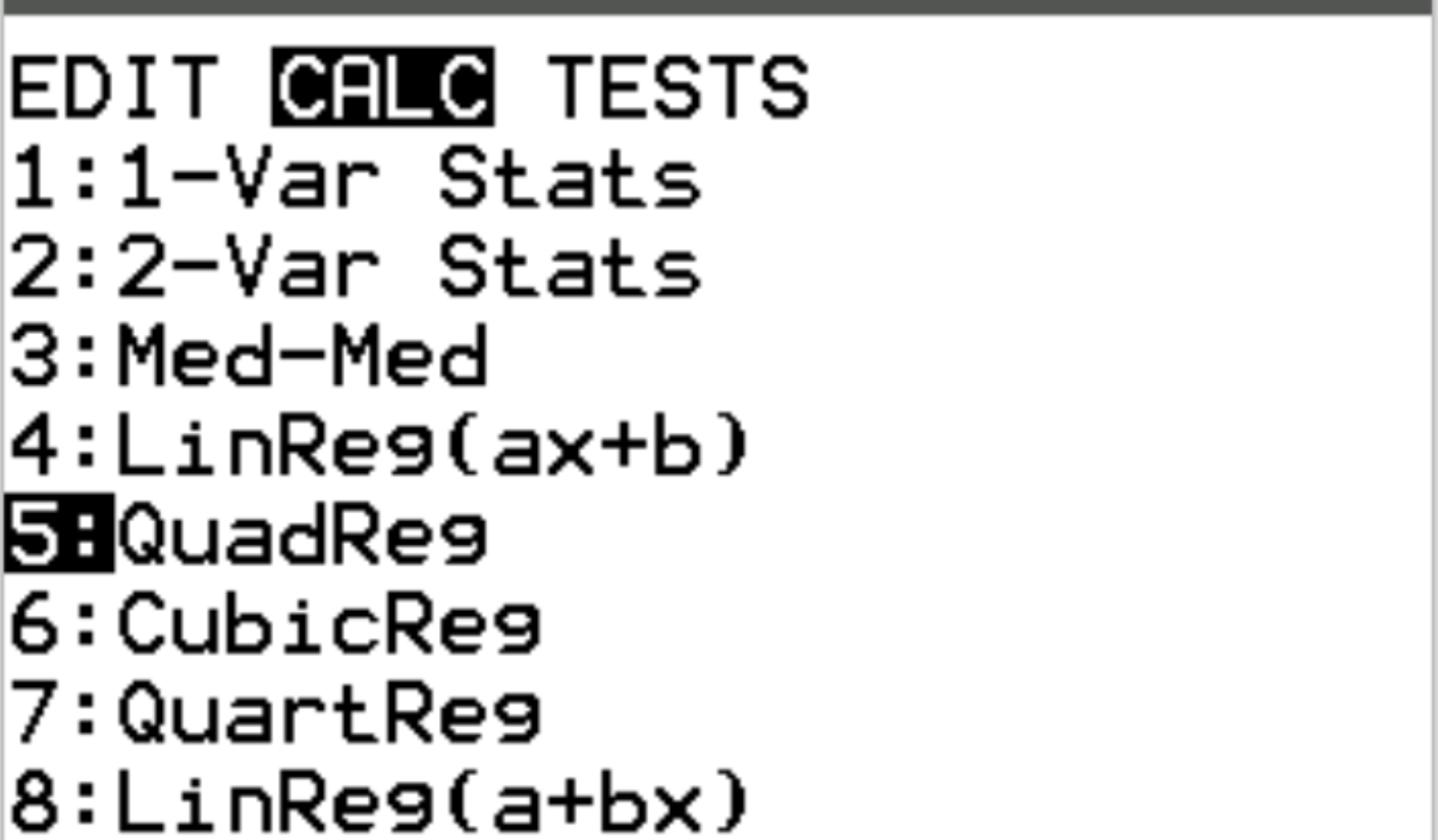
بالنسبة إلى Xlist وYlist، تأكد من تحديد L1 وL2 لأن هذه هي الأعمدة التي استخدمناها لإدخال بياناتنا. اترك قائمة التكرارات فارغة. قم بالتمرير لأسفل إلى “حساب” ثم اضغط على “إدخال” .

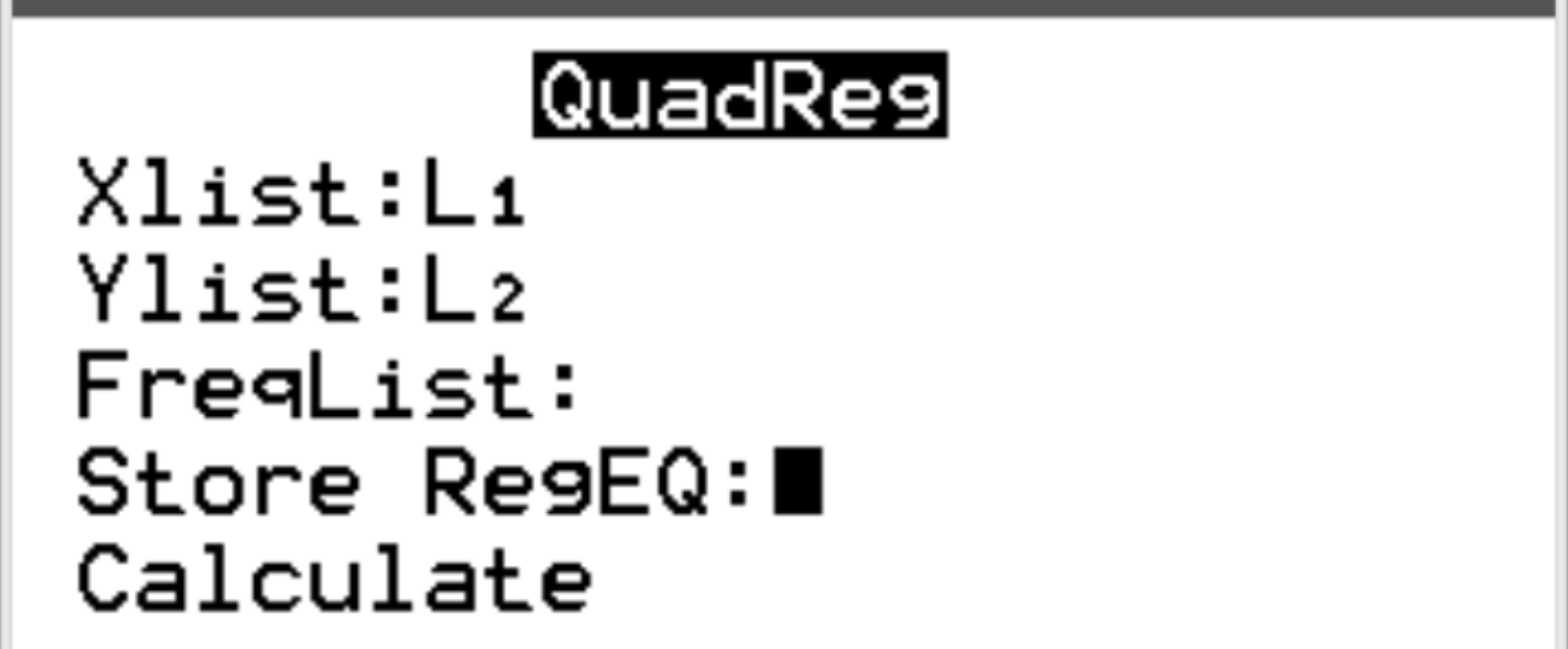
سيظهر الإخراج التالي تلقائيًا:

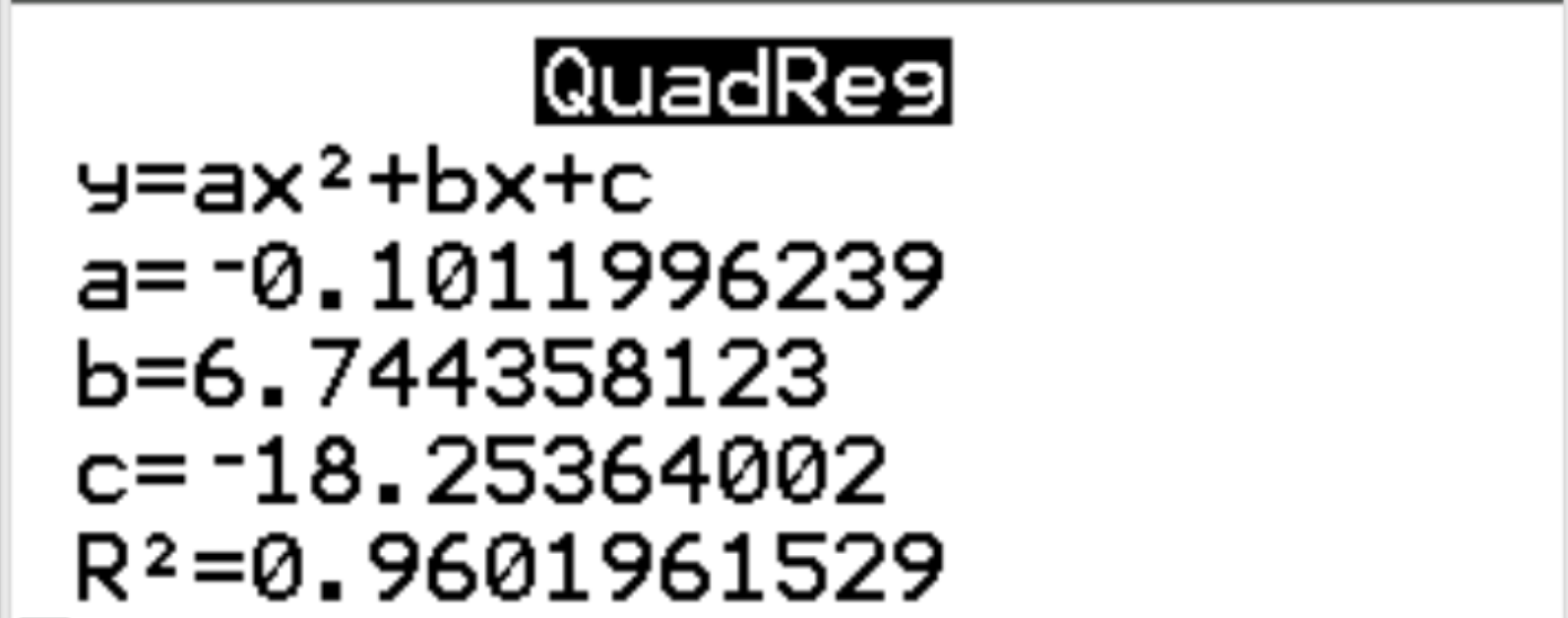
الخطوة 3: تفسير النتيجة.

ومن النتائج يتبين لنا أن معادلة الانحدار المقدرة هي:

السعادة = -0.1012 (ساعة) ² + 6.7444 (ساعة) – 18.2536

يمكننا استخدام هذه المعادلة للعثور على السعادة المتوقعة للفرد، بالنظر إلى عدد الساعات التي يعملها في الأسبوع.

على سبيل المثال، الشخص الذي يعمل 60 ساعة في الأسبوع سيكون لديه مستوى سعادة يبلغ 22.09 :

السعادة = -0.1012(60) ² + 6.7444(60) – 18.2536 = 22.09

وعلى العكس من ذلك، فإن الشخص الذي يعمل 30 ساعة أسبوعيًا يجب أن يكون مستوى سعادته 92.99 :

السعادة = -0.1012(30) ² + 6.7444(30) – 18.2536 = 92.99

يمكننا أيضًا أن نرى أن مربع r لنموذج الانحدار هو r ² = 0.9602 . وهي نسبة التباين في متغير الاستجابة التي يمكن تفسيرها بالمتغيرات التوضيحية. في هذا المثال، يمكن تفسير 96.02% من التباين في السعادة بالساعات والأوقات ² .