كيفية حساب درجات z في إكسل

في الإحصائيات، تخبرنا النتيجة z عن عدد الانحرافات المعيارية للقيمة عن المتوسط . نستخدم الصيغة التالية لحساب درجة z:

ض = (X – μ) / σ

ذهب:

• X هي قيمة بيانات أولية واحدة
• μ هو متوسط مجموعة البيانات
• σ هو الانحراف المعياري لمجموعة البيانات

يشرح هذا البرنامج التعليمي كيفية حساب نقاط z لقيم البيانات الأولية في Excel.

كيفية حساب درجات Z في إكسيل

لنفترض أن لدينا مجموعة البيانات التالية ونريد العثور على درجة z لكل قيمة بيانات أولية:

يمكننا تنفيذ الخطوات التالية للقيام بذلك.

الخطوة 1: ابحث عن المتوسط والانحراف المعياري لمجموعة البيانات.

أولاً، نحتاج إلى إيجاد المتوسط والانحراف المعياري لمجموعة البيانات. توضح الصيغ التالية كيفية القيام بذلك:

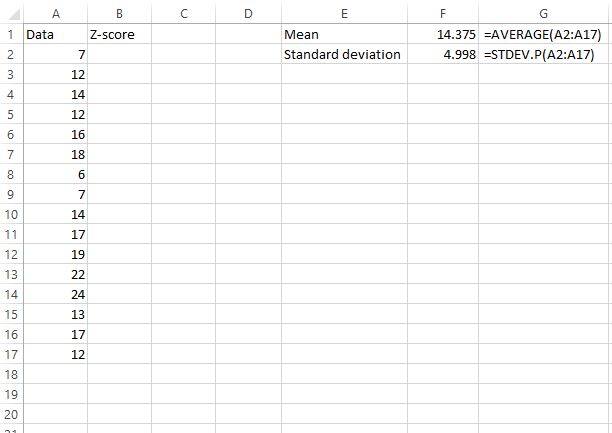
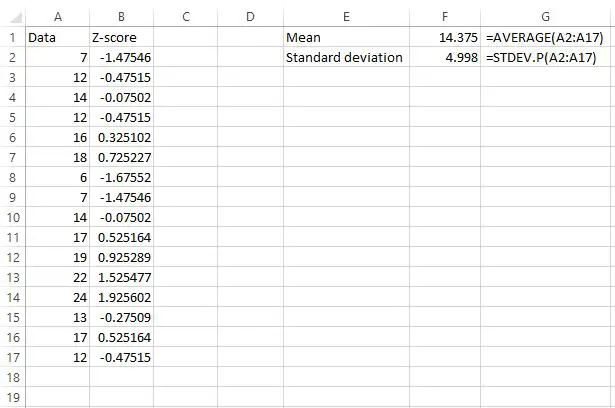
المتوسط هو 14.375 والانحراف المعياري هو 4.998 .

الخطوة 2: ابحث عن النتيجة z لقيمة البيانات الأولية الأولى.

بعد ذلك، سنجد درجة z لقيمة البيانات الأولية الأولى باستخدام الصيغة z = (X – μ) / σ.

تعرض الخلية C2 الصيغة التي استخدمناها لحساب قيمة z في الخلية B2.

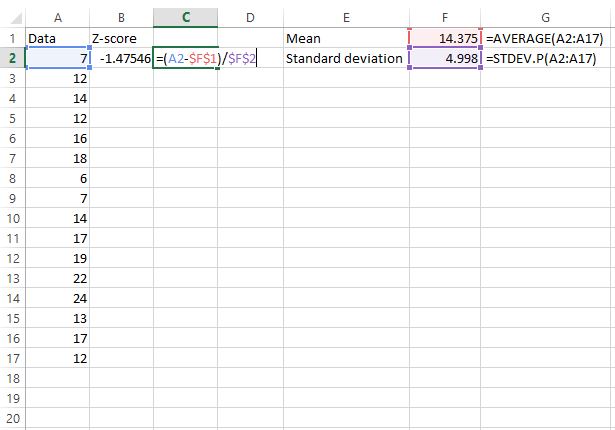
الخطوة 3: ابحث عن درجات z لجميع القيم المتبقية.

الآن بعد أن وجدنا النتيجة z للقيمة الأولى في مجموعة البيانات، يمكننا ببساطة نسخ الصيغة التي استخدمناها في الخلية B2 إلى بقية قيم البيانات. يمكننا القيام بذلك عن طريق تحديد عمود درجة z بالكامل، بدءًا من درجة z الأولى التي قمنا بحسابها بالفعل:

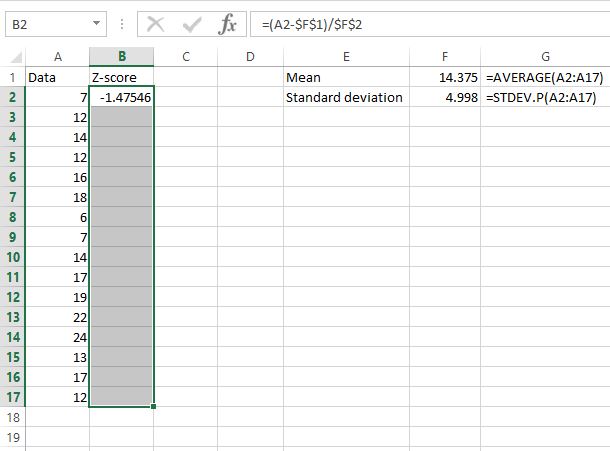
بعد ذلك، اضغط على Ctrl+D . يؤدي هذا إلى نسخ الصيغة من الخلية الأولى إلى كافة الخلايا الموجودة أسفلها.

لقد وجدنا الآن درجة z لكل قيمة بيانات أولية.

كيفية تفسير درجات Z في Excel

تذكر أن النتيجة z تخبرنا ببساطة بعدد الانحرافات المعيارية للقيمة عن المتوسط.

يمكن أن تكون النتيجة Z إيجابية أو سلبية أو صفر.

تشير درجة z الإيجابية إلى أن قيمة معينة أعلى من المتوسط، وتشير درجة z السالبة إلى أن قيمة معينة أقل من المتوسط، وتشير درجة الصفر من الألف إلى الياء إلى أن قيمة معينة تساوي المتوسط.

في مثالنا، وجدنا أن المتوسط كان 14.375 والانحراف المعياري كان 4.998 .

لذا فإن القيمة الأولى في مجموعة البيانات الخاصة بنا كانت 7، والتي حصلت على درجة Z (7-14.375) / 4.998 = -1.47546 . وهذا يعني أن القيمة “7” هي -1.47545 انحرافات معيارية أقل من المتوسط.

القيمة التالية في بياناتنا، 12، حصلت على درجة Z (12-14.375) / 4.998 = -0.47515 . وهذا يعني أن القيمة “12” هي -0.47515 انحرافات معيارية أقل من المتوسط.

كلما كانت القيمة أبعد عن المتوسط، كلما ارتفعت القيمة المطلقة لدرجة z لتلك القيمة.

على سبيل المثال، القيمة 7 أبعد عن المتوسط (14.375) من القيمة 12، وهو ما يفسر سبب حصول 7 على درجة z ذات قيمة مطلقة أكبر.

مصادر إضافية

توفر المقالات التالية معلومات إضافية حول كيفية العمل مع نتائج z في Excel:

كيفية العثور على قيمة P من Z Score في Excel
كيفية التحويل بين درجات Z والنسب المئوية في Excel