كيفية حساب نقاط z على الآلة الحاسبة ti-84

تخبرنا النتيجة z بعدد الانحرافات المعيارية لقيمة معينة عن المتوسط. يتم حساب درجة z لقيمة معينة على النحو التالي:

النتيجة z = (x – μ) / σ

ذهب:

• س: القيمة الفردية
• μ: متوسط عدد السكان
• σ : الانحراف المعياري للسكان

يشرح هذا البرنامج التعليمي كيفية حساب درجات z على الآلة الحاسبة TI-84.

كيفية حساب النتيجة Z لقيمة واحدة

لنفترض أن التوزيع يتم توزيعه بشكل طبيعي بمتوسط 12 وانحراف معياري قدره 1.4 ونريد حساب الدرجة z لقيمة فردية x = 14. لحساب الدرجة z في الآلة الحاسبة TI-84، سنقوم ببساطة اكتب الصيغة التالية:

يخبرنا هذا أن القيمة الفردية 14 لها درجة Z تبلغ 1.4286 . بمعنى آخر، القيمة 14 هي 1.4286 انحراف معياري فوق المتوسط.

كيفية حساب درجة Z لقيم متعددة

بدلًا من ذلك، لنفترض أن لدينا قائمة بقيم البيانات ونريد حساب درجة z لكل قيمة في القائمة. وفي هذه الحالة يمكننا القيام بالخطوات التالية:

الخطوة 1: أدخل البيانات.

أولا، سوف نقوم بإدخال قيم البيانات. اضغط على Stat ثم اضغط على EDIT . أدخل القيم التالية في العمود L1:

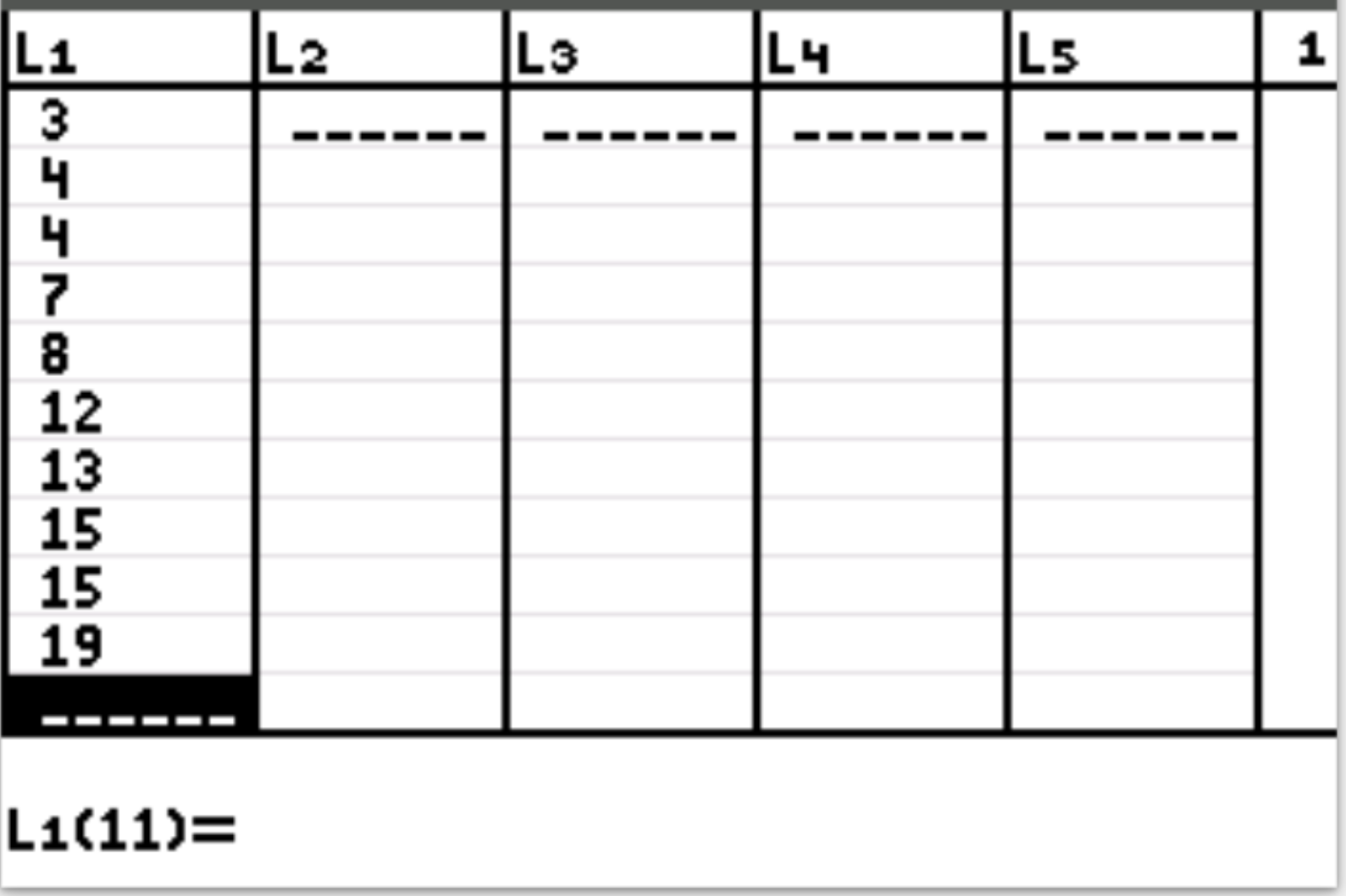
الخطوة 2: ابحث عن المتوسط والانحراف المعياري لقيم البيانات.

بعد ذلك، سوف نجد المتوسط والانحراف المعياري لمجموعة البيانات. اضغط على Stat ثم قم بالتمرير إلى CALC . قم بتمييز الإحصائيات 1-Var ثم اضغط على Enter .

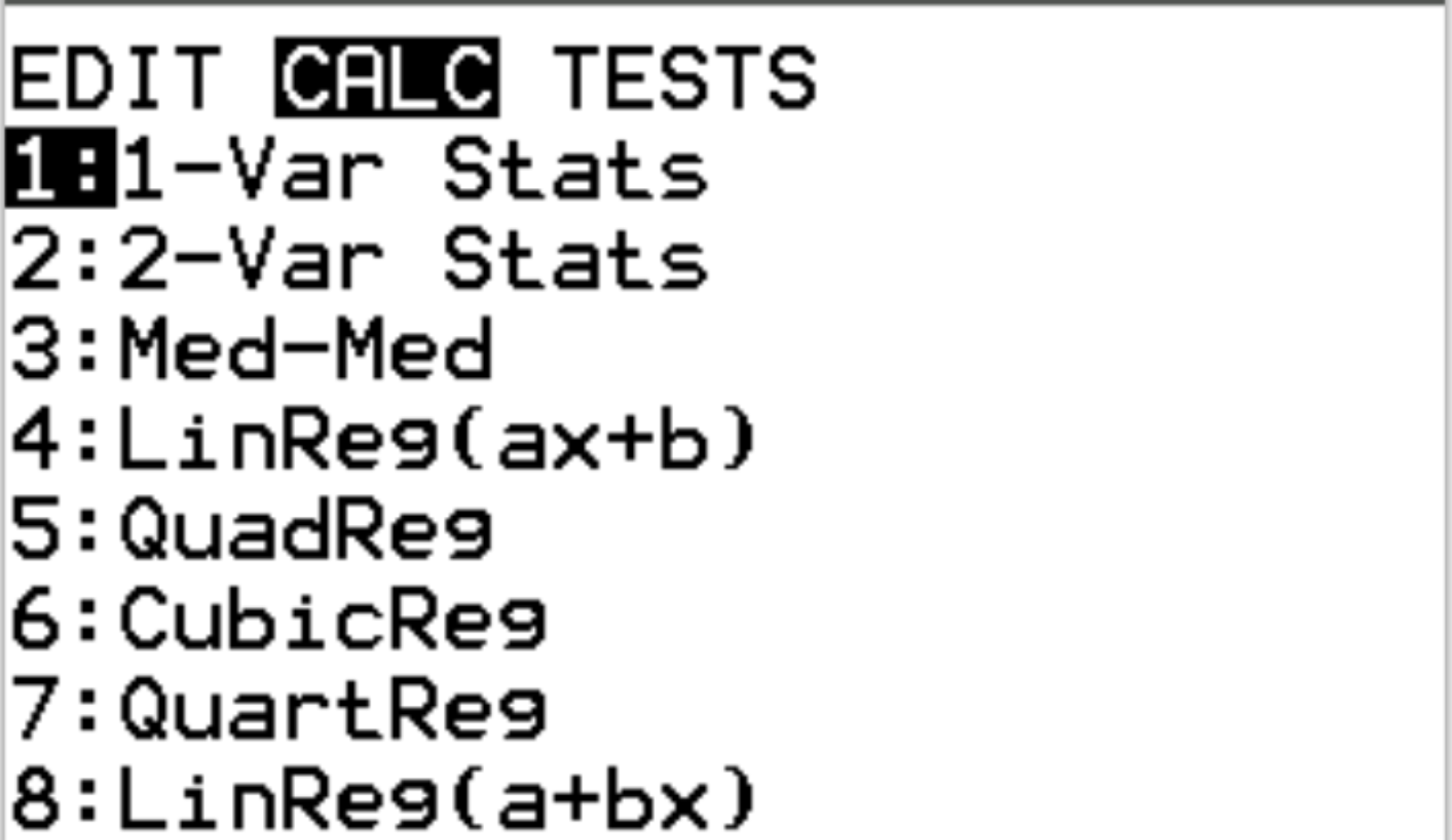
بالنسبة إلى القائمة ، تأكد من اختيار L1 نظرًا لأن هذا هو العمود الذي أدخلنا بياناتنا فيه. اترك قائمة التكرارات فارغة. قم بتمييز “حساب” ثم اضغط على “إدخال” .

سيظهر الإخراج التالي:

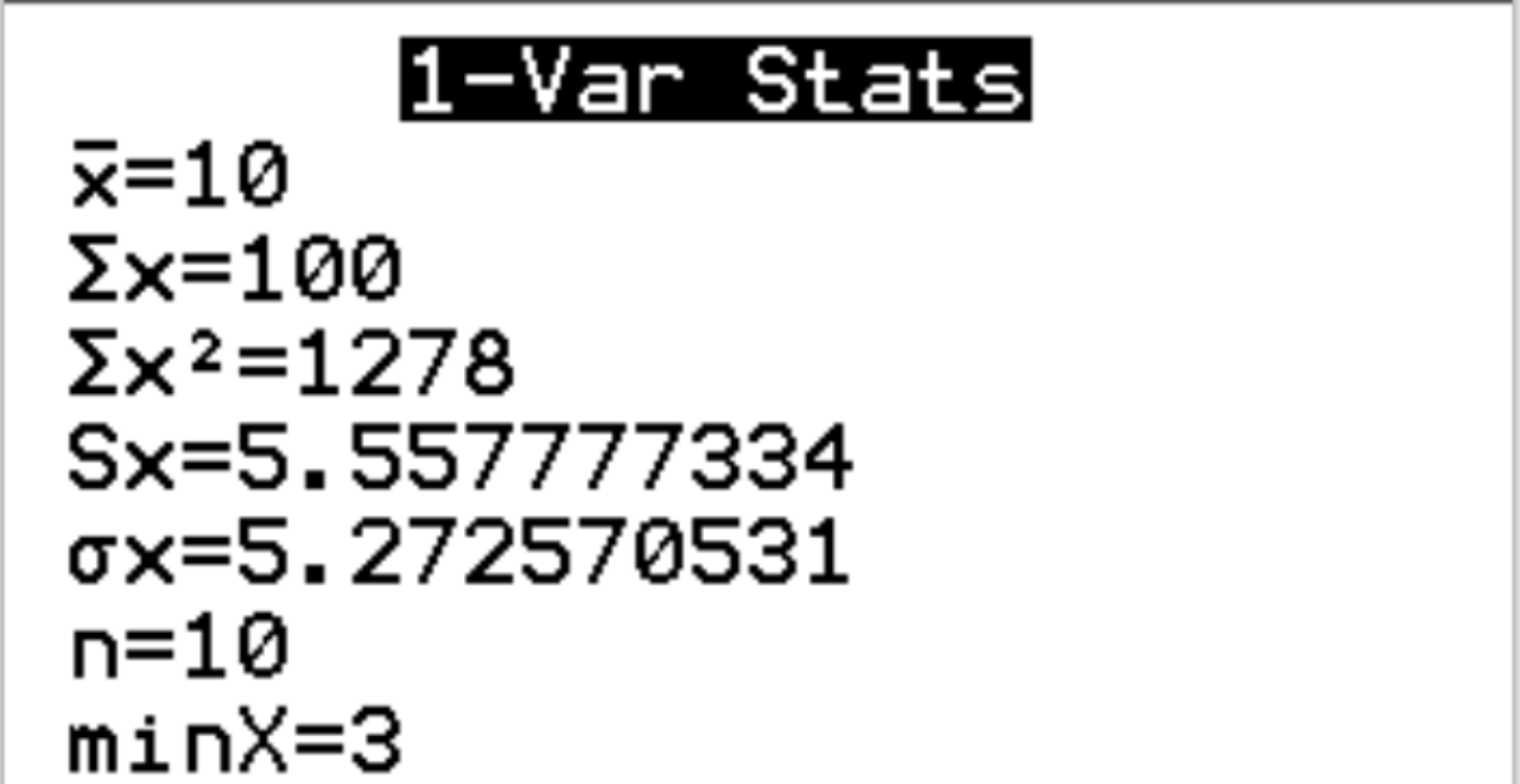
يمكننا أن نرى أن متوسط مجموعة البيانات هو x = 10 والانحراف المعياري هو s _x = 5.558 . سوف نستخدم هاتين القيمتين في الخطوة التالية لحساب درجات z.

الخطوة 3: استخدم صيغة لحساب كل درجة Z.

بعد ذلك، سنقوم بحساب درجة z لكل قيمة فردية في مجموعة البيانات. اضغط على Stat ثم اضغط على EDIT . قم بتمييز L2 واكتب الصيغة ( L1-10)/5.558 ، ثم اضغط على Enter . ستظهر النتيجة z لكل قيمة فردية تلقائيًا في العمود L2:

ملاحظة: لإدخال “L1” في الصيغة، اضغط على 2 ثم اضغط على 1 .

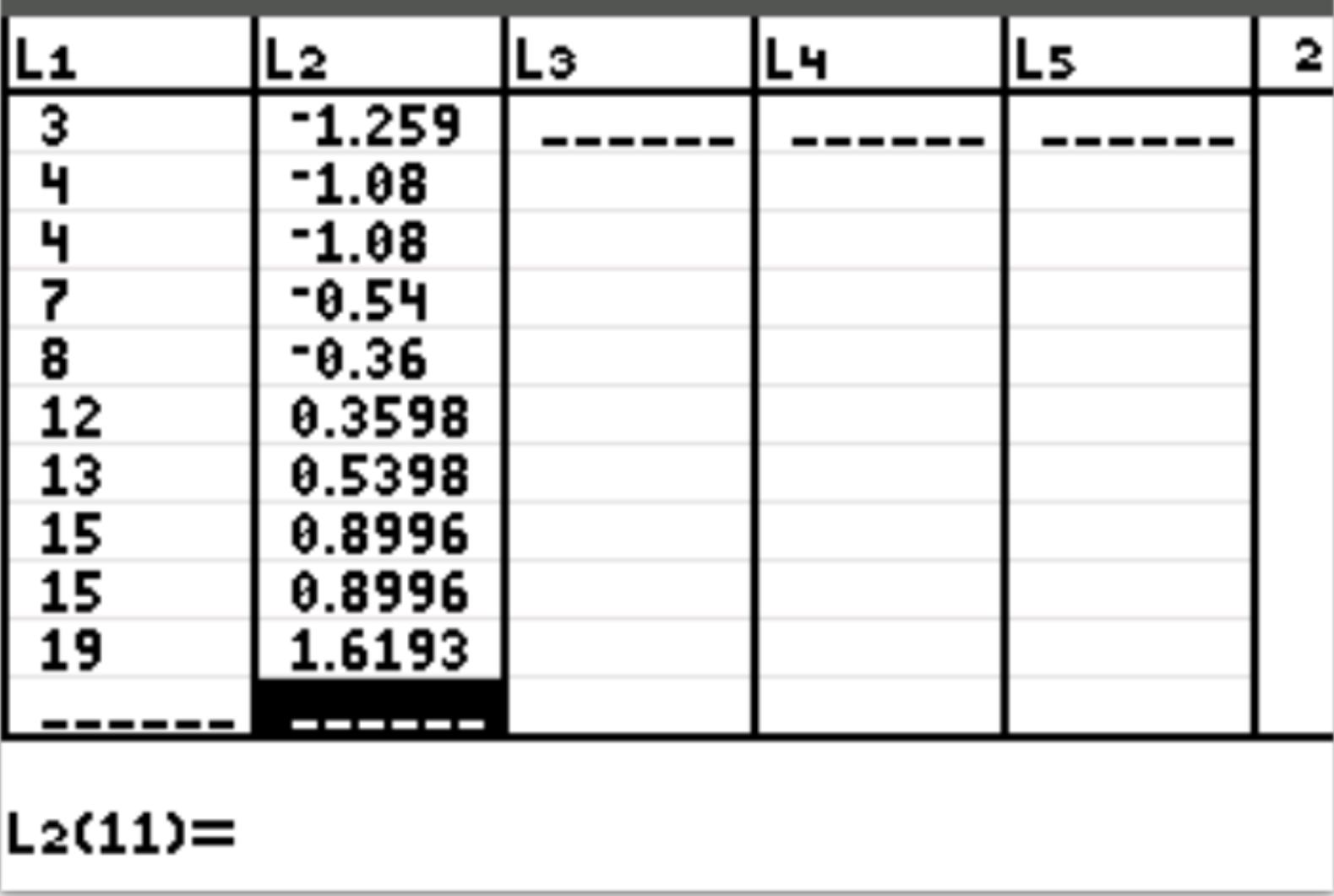
كيفية تفسير درجات Z

تذكر أن النتيجة z تخبرنا ببساطة بعدد الانحرافات المعيارية للقيمة عن المتوسط. يمكن أن تكون النتيجة Z إيجابية أو سلبية أو تساوي الصفر:

• تشير درجة z الإيجابية إلى أن قيمة معينة أعلى من المتوسط.
• تشير درجة z السلبية إلى أن قيمة معينة أقل من المتوسط.
• تشير درجة z التي تبلغ صفر إلى أن قيمة معينة تساوي المتوسط.

في مثالنا، وجدنا أن المتوسط كان 10 والانحراف المعياري كان 5.558 .

لذا فإن القيمة الأولى في مجموعة البيانات الخاصة بنا كانت 3، والتي كانت لها درجة Z (3-10)/5.558 = -1.259 . وهذا يعني أن القيمة “3” هي 1.259 انحراف معياري أقل من المتوسط.

القيمة التالية في مجموعة البيانات لدينا، 4، حصلت على درجة Z (4-10) / 5.558 = -1.08 . وهذا يعني أن القيمة “4” هي 1.08 انحراف معياري أقل من المتوسط.

كلما كانت القيمة أبعد عن المتوسط، كلما ارتفعت القيمة المطلقة لدرجة z لتلك القيمة.

على سبيل المثال، القيمة 3 أبعد عن المتوسط من القيمة 4، وهو ما يفسر سبب حصول 3 على درجة z ذات قيمة مطلقة أكبر.