كيفية حساب نتائج z في جداول بيانات google

في الإحصائيات، تخبرنا النتيجة z عن عدد الانحرافات المعيارية للقيمة عن المتوسط . نستخدم الصيغة التالية لحساب درجة z:

ض = (X – μ) / σ

ذهب:

• X هي قيمة بيانات أولية واحدة
• μ هو متوسط مجموعة البيانات
• σ هو الانحراف المعياري لمجموعة البيانات

يشرح هذا البرنامج التعليمي كيفية حساب نقاط z لقيم البيانات الأولية في جداول بيانات Google.

مثال: نتائج z في جداول بيانات Google

لنفترض أن لدينا مجموعة البيانات التالية ونريد العثور على درجة z لكل قيمة بيانات أولية:

يمكننا تنفيذ الخطوات التالية للقيام بذلك.

الخطوة 1: ابحث عن المتوسط والانحراف المعياري لمجموعة البيانات.

أولاً، نحتاج إلى إيجاد المتوسط والانحراف المعياري لمجموعة البيانات. توضح الصيغ التالية كيفية القيام بذلك:

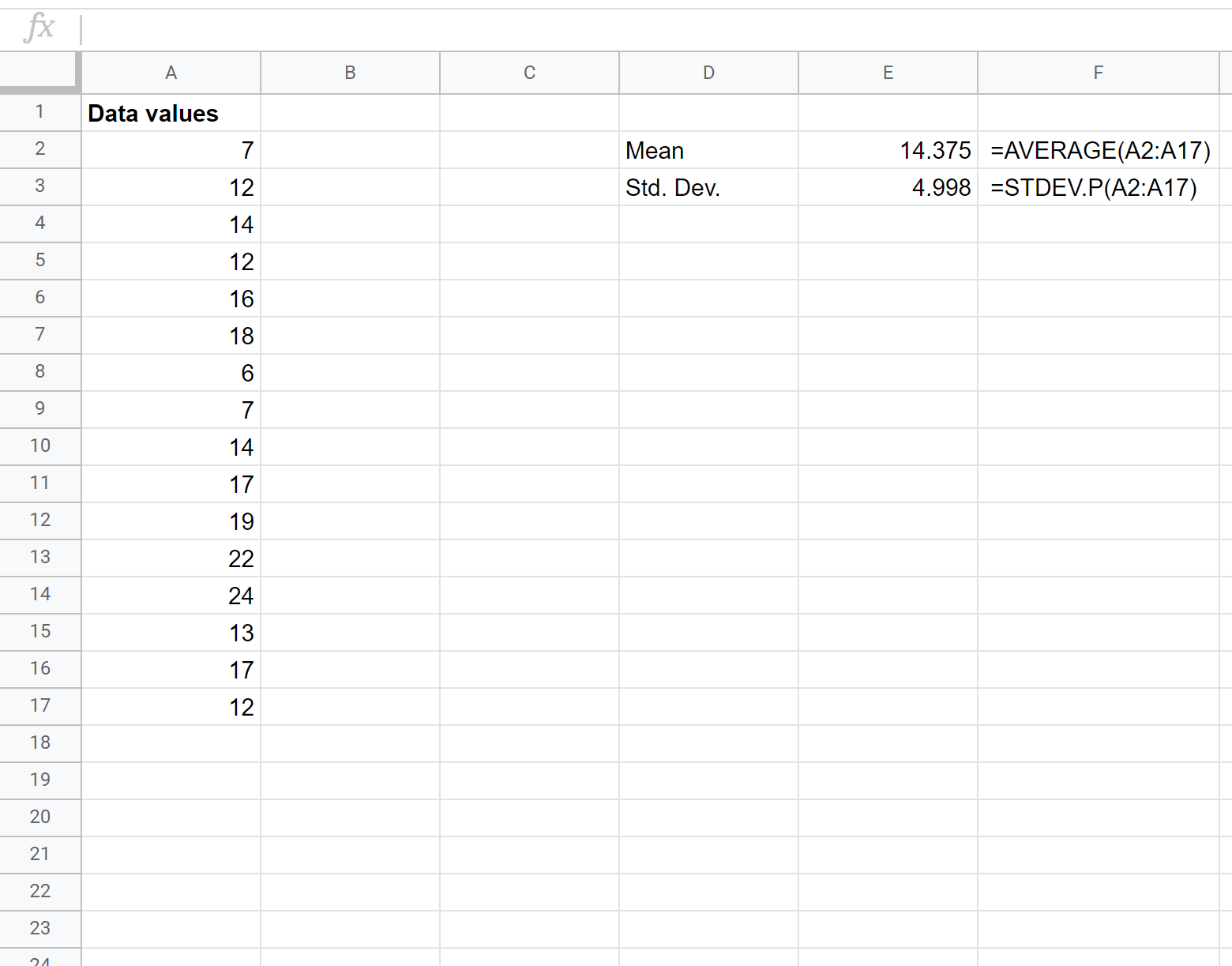
المتوسط هو 14.375 والانحراف المعياري هو 4.998 .

الخطوة 2: ابحث عن النتيجة z لقيمة البيانات الأولية الأولى.

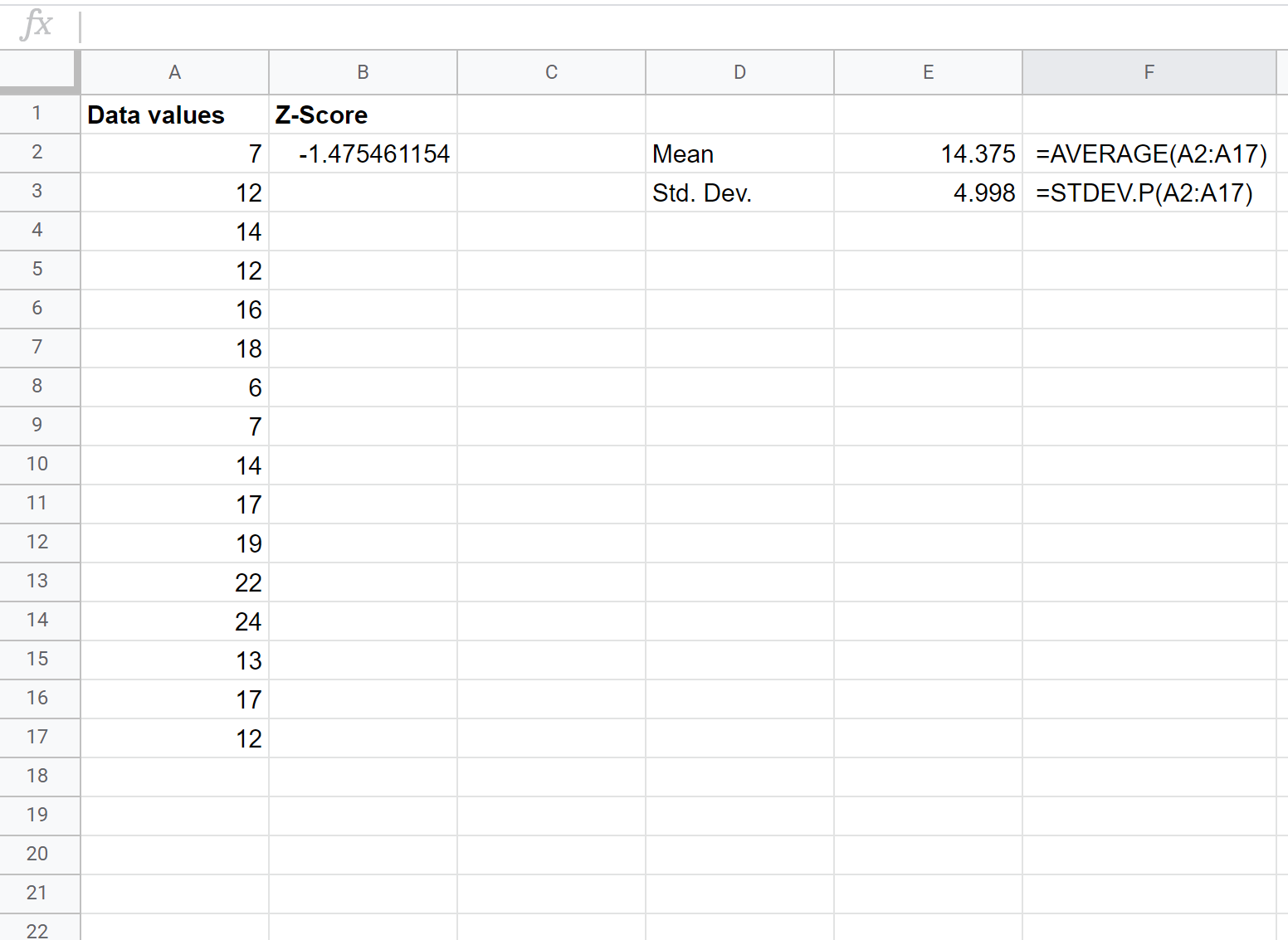
بعد ذلك، سوف نجد درجة z لقيمة البيانات الأولية الأولى عن طريق كتابة الصيغة التالية في الخلية B2:

= ( A2 – $E$2 ) / $E$3

الخطوة 3: ابحث عن درجات z لجميع القيم المتبقية.

بمجرد قيامنا بحساب النتيجة z الأولى، يمكننا تمييز بقية العمود B بدءًا من الخلية B2 والضغط على Ctrl+D لنسخ الصيغة من الخلية B2 إلى كل خلية من الخلايا أدناه:

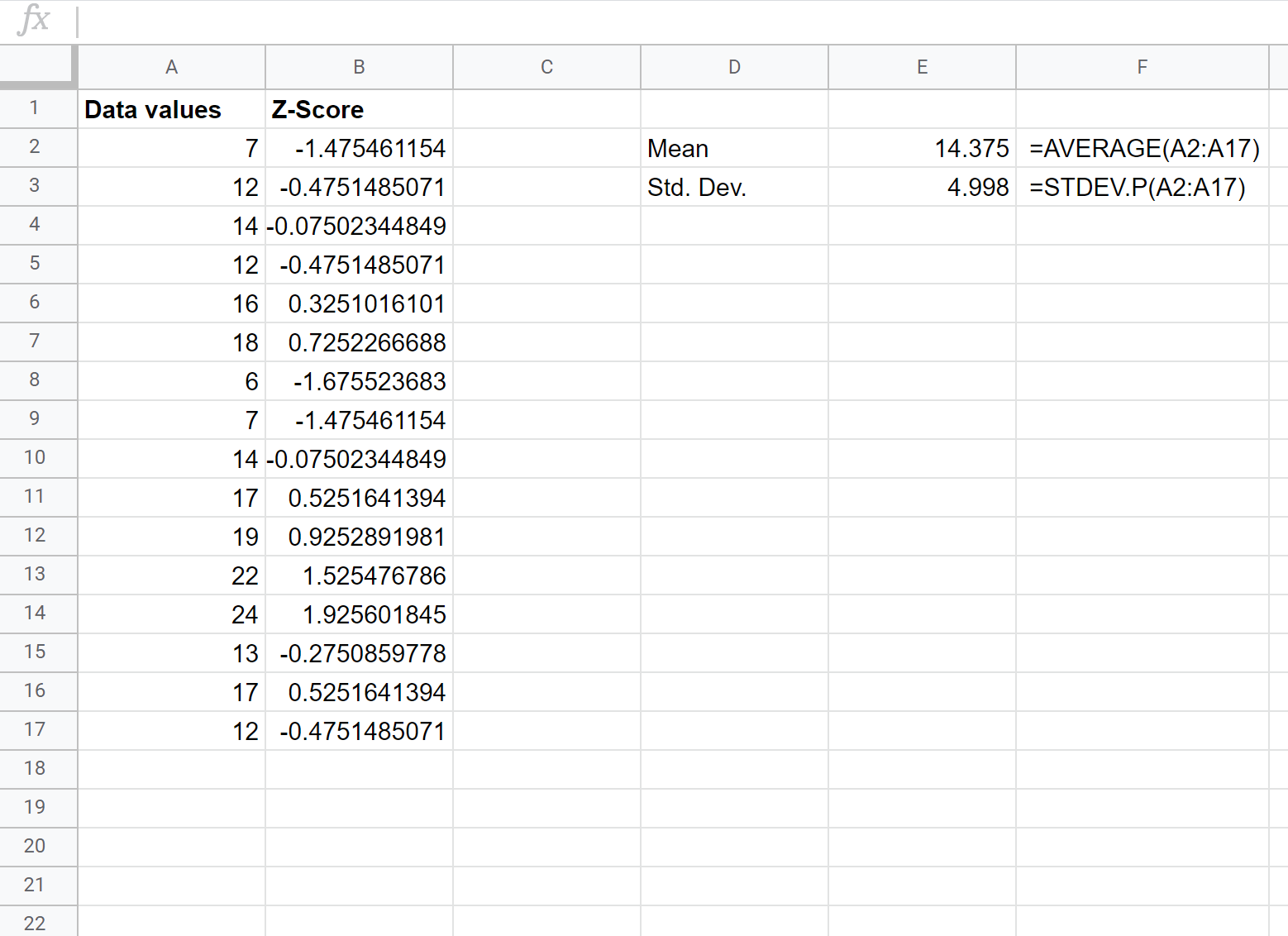
لقد وجدنا الآن درجة z لكل قيمة بيانات أولية.

كيفية تفسير درجات Z

تخبرنا النتيجة z ببساطة بعدد الانحرافات المعيارية للقيمة عن المتوسط.

في مثالنا، وجدنا أن المتوسط كان 14.375 والانحراف المعياري كان 4.998 .

لذا فإن القيمة الأولى في مجموعة البيانات الخاصة بنا كانت 7، والتي حصلت على درجة Z (7-14.375) / 4.998 = -1.47546 . وهذا يعني أن القيمة “7” هي -1.47545 انحرافات معيارية أقل من المتوسط.

القيمة التالية في بياناتنا، 12، حصلت على درجة Z (12-14.375) / 4.998 = -0.47515 . وهذا يعني أن القيمة “12” هي -0.47515 انحرافات معيارية أقل من المتوسط.

كلما كانت القيمة أبعد عن المتوسط، كلما ارتفعت القيمة المطلقة لدرجة z لتلك القيمة. على سبيل المثال، القيمة 7 أبعد عن المتوسط (14.375) من القيمة 12، وهو ما يفسر سبب حصول 7 على درجة z ذات قيمة مطلقة أكبر.

مصادر إضافية

كيفية حساب درجات Z في إكسيل
كيفية حساب درجات Z في R
كيفية حساب نقاط Z على الآلة الحاسبة TI-84