تحليل التباين أحادي الاتجاه: التعريف والصيغة والمثال
يقارن ANOVA أحادي الاتجاه (“تحليل التباين”) بين متوسطات ثلاث مجموعات مستقلة أو أكثر لتحديد ما إذا كان هناك فرق ذو دلالة إحصائية بين متوسطات المجموعة السكانية المقابلة.
يشرح هذا البرنامج التعليمي ما يلي:
- الدافع لأداء ANOVA في اتجاه واحد.
- الافتراضات التي يجب الوفاء بها لإجراء تحليل التباين أحادي الاتجاه.
- عملية إجراء تحليل التباين (ANOVA) أحادي الاتجاه.
- مثال على كيفية إجراء تحليل التباين الأحادي (ANOVA) أحادي الاتجاه.
ANOVA في اتجاه واحد: الدافع
لنفترض أننا نريد أن نعرف ما إذا كانت ثلاثة برامج مختلفة للتحضير للاختبار تؤدي إلى متوسط درجات مختلفة في امتحان القبول بالجامعة أم لا. نظرًا لوجود الملايين من طلاب المدارس الثانوية في جميع أنحاء البلاد، فسيكون الأمر مستهلكًا للوقت ومكلفًا للغاية للذهاب إلى كل طالب والسماح لهم باستخدام أحد برامج الإعداد للاختبار.
بدلاً من ذلك، يمكننا اختيار ثلاث عينات عشوائية مكونة من 100 طالب من المجتمع والسماح لكل عينة باستخدام أحد برامج الإعداد للاختبار الثلاثة للتحضير للامتحان. ومن ثم يمكننا تسجيل درجات كل طالب بمجرد تقديمه للامتحان.
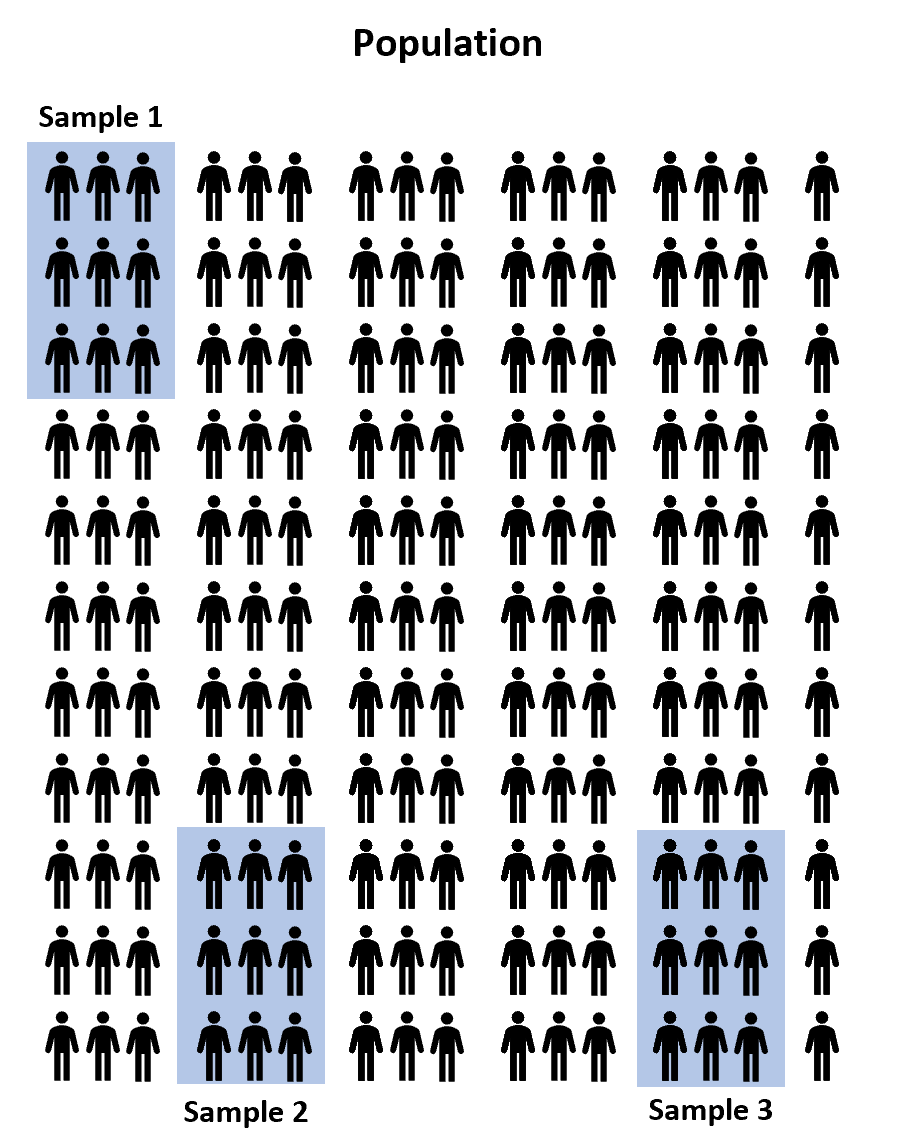
ومع ذلك، فمن المؤكد تقريبًا أن متوسط درجات الاختبار بين العينات الثلاث سيكون مختلفًا قليلاً على الأقل. والسؤال هو ما إذا كان هذا الاختلاف ذو دلالة إحصائية . ولحسن الحظ، فإن تحليل التباين أحادي الاتجاه يسمح لنا بالإجابة على هذا السؤال.
ANOVA أحادي الاتجاه: الافتراضات
لكي تكون نتائج تحليل التباين الأحادي صحيحة، يجب استيفاء الافتراضات التالية:
1. الحالة الطبيعية – تم أخذ كل عينة من مجتمع موزع بشكل طبيعي.
2. التباينات المتساوية – تباينات المجتمعات التي تم سحب العينات منها متساوية. يمكنك استخدام اختبار بارتليت لاختبار هذه الفرضية.
3. الاستقلال – الملاحظات داخل كل مجموعة مستقلة عن بعضها البعض وتم الحصول على الملاحظات داخل المجموعات عن طريق أخذ عينات عشوائية.
اقرأ هذه المقالة لمزيد من التفاصيل حول كيفية التحقق من هذه الافتراضات.
ANOVA في اتجاه واحد: العملية
يستخدم تحليل التباين الأحادي الفرضيات الصفرية والبديلة التالية:
- H 0 (فرضية العدم): μ 1 = μ 2 = μ 3 = … = μ k (جميع الوسائل السكانية متساوية)
- H 1 (فرضية بديلة): هناك متوسط سكاني واحد على الأقل مختلف استراحة
ستستخدم عادةً بعض البرامج الإحصائية (مثل R وExcel وStata وSPSS وما إلى ذلك) لإجراء تحليل التباين أحادي الاتجاه نظرًا لصعوبة تنفيذه يدويًا.
بغض النظر عن البرنامج الذي تستخدمه، سوف تتلقى الجدول التالي كمخرج:
| مصدر | مجموع المربعات (SS) | df | متوسط المربعات (MS) | F | ص |
|---|---|---|---|---|---|
| علاج | آر إس إس | مدافع ص | إم إس آر | MSR/MSE | و مدافع ص , مدافع ه |
| خطأ | وفاق سطيف | مدافع ه | MSE | ||
| مجموع | الصحة والسلامة المهنية | مدافع ر |
ذهب:
- SSR: مجموع انحدار المربعات
- SSE: مجموع الخطأ التربيعي
- SST: مجموع المربعات (SST = SSR + SSE)
- df r : درجات انحدار الحرية (df r = k-1)
- df e : درجات الخطأ في الحرية (df e = nk)
- df t : مجموع درجات الحرية (df t = n-1)
- ك: العدد الإجمالي للمجموعات
- ن: مجموع الملاحظات
- MSR: متوسط الانحدار المربع (MSR = SSR/df r )
- MSE: متوسط مربع الخطأ (MSE = SSE/df e )
- F: إحصائية اختبار F (F = MSR/MSE)
- p: القيمة p التي تقابل F dfr, dfe
إذا كانت القيمة p أقل من مستوى الأهمية المختار (على سبيل المثال 0.05)، فيمكنك رفض فرضية العدم والاستنتاج بأن واحدًا على الأقل من متوسطات المجتمع يختلف عن الآخرين.
ملاحظة: إذا رفضت الفرضية الصفرية، فهذا يشير إلى أن واحدًا على الأقل من متوسطات السكان يختلف عن المتوسطات الأخرى، لكن جدول تحليل التباين (ANOVA) لا يحدد أي متوسطات المجتمع مختلفة. لتحديد ذلك، تحتاج إلى إجراء اختبار ما بعد المخصص ، ويسمى أيضًا اختبار “المقارنة المتعددة”.
تحليل التباين أحادي الاتجاه: مثال
لنفترض أننا نريد أن نعرف ما إذا كانت ثلاثة برامج مختلفة للتحضير للاختبار تؤدي إلى متوسط درجات مختلفة في اختبار معين أم لا. ولاختبار ذلك، قمنا بتجنيد 30 طالبًا للمشاركة في إحدى الدراسات وتقسيمهم إلى ثلاث مجموعات.
يتم تعيين الطلاب في كل مجموعة عشوائيًا لاستخدام أحد برامج التحضير للاختبار الثلاثة للأسابيع الثلاثة التالية للتحضير للامتحان. وفي نهاية الأسابيع الثلاثة، يؤدي جميع الطلاب نفس الاختبار.
وفيما يلي نتائج الامتحانات لكل مجموعة:

لإجراء تحليل التباين أحادي الاتجاه على هذه البيانات، سنستخدم حاسبة التباين الإحصائي أحادي الاتجاه مع الإدخال التالي:

من جدول الإخراج، نرى أن إحصائيات اختبار F هي 2.358 والقيمة p المقابلة هي 0.11385 .

وبما أن هذه القيمة p لا تقل عن 0.05، فإننا نفشل في رفض فرضية العدم.
وهذا يعني أنه ليس لدينا أدلة كافية لنقول بوجود فرق ذي دلالة إحصائية بين متوسط درجات الامتحانات للمجموعات الثلاث.
مصادر إضافية
تشرح المقالات التالية كيفية إجراء تحليل التباين أحادي الاتجاه باستخدام برامج إحصائية مختلفة:
كيفية إجراء ANOVA أحادي الاتجاه في Excel
كيفية إجراء ANOVA أحادي الاتجاه في R
كيفية إجراء ANOVA أحادي الاتجاه في بايثون
كيفية إجراء ANOVA أحادي الاتجاه في SAS
كيفية إجراء تحليل التباين أحادي الاتجاه في برنامج SPSS
كيفية إجراء ANOVA أحادي الاتجاه في Stata
كيفية إجراء تحليل التباين أحادي الاتجاه على الآلة الحاسبة TI-84
حاسبة تحليل التباين (ANOVA) عبر الإنترنت في اتجاه واحد