كيفية إجراء اختبار t من عينتين على الآلة الحاسبة ti-84
يتم استخدام اختبار t المكون من عينتين لاختبار ما إذا كانت متوسطات مجتمعين متساويتين أم لا.
يشرح هذا البرنامج التعليمي كيفية إجراء اختبار t المكون من عينتين على الآلة الحاسبة TI-84.
مثال: اختبار t لعينتين على الآلة الحاسبة TI-84
يريد الباحثون معرفة ما إذا كانت المعالجة الجديدة للوقود تؤدي إلى تغيير في متوسط ميل لكل جالون في سيارة معينة. ولاختبار ذلك، أجروا تجربة حيث تلقت 12 سيارة معالجة الوقود الجديدة و12 سيارة لم تحصل عليها. بالنسبة لمجموعة التحكم، متوسط ميل لكل جالون هو 21 ميل لكل جالون والانحراف المعياري هو 2.73 ميل لكل جالون. بالنسبة لمجموعة العلاج، متوسط ميلا في الغالون هو 22.75 ميلا في الغالون والانحراف المعياري هو 3.25 ميلا في الغالون.
استخدم هذه البيانات لإجراء اختبار t من عينتين لتحديد ما إذا كان متوسط ميل لكل جالون مختلفًا بين المجموعتين.
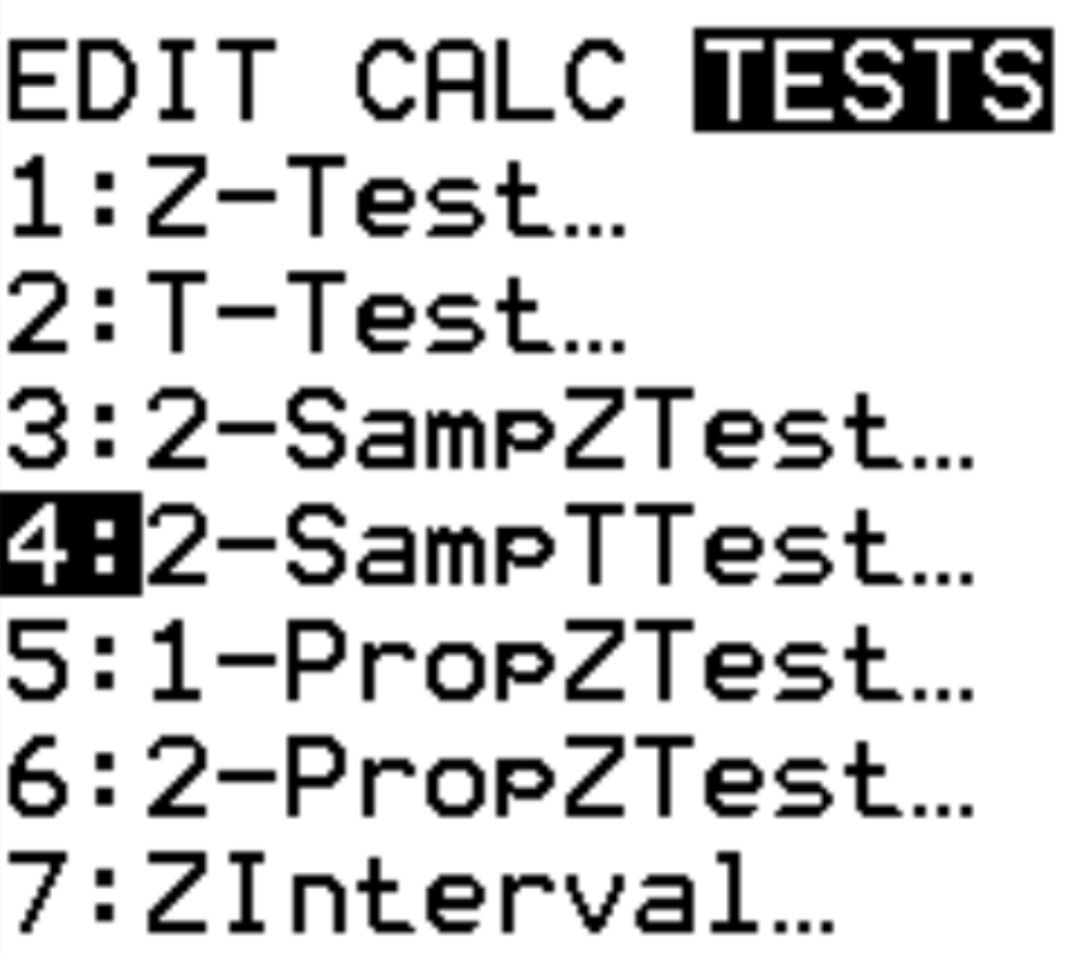
الخطوة 1: حدد 2-SampTTest.
اضغط على الإحصائيات . قم بالتمرير لأسفل إلى الاختبارات. قم بالتمرير إلى 2-SampTTest ثم اضغط على ENTER .
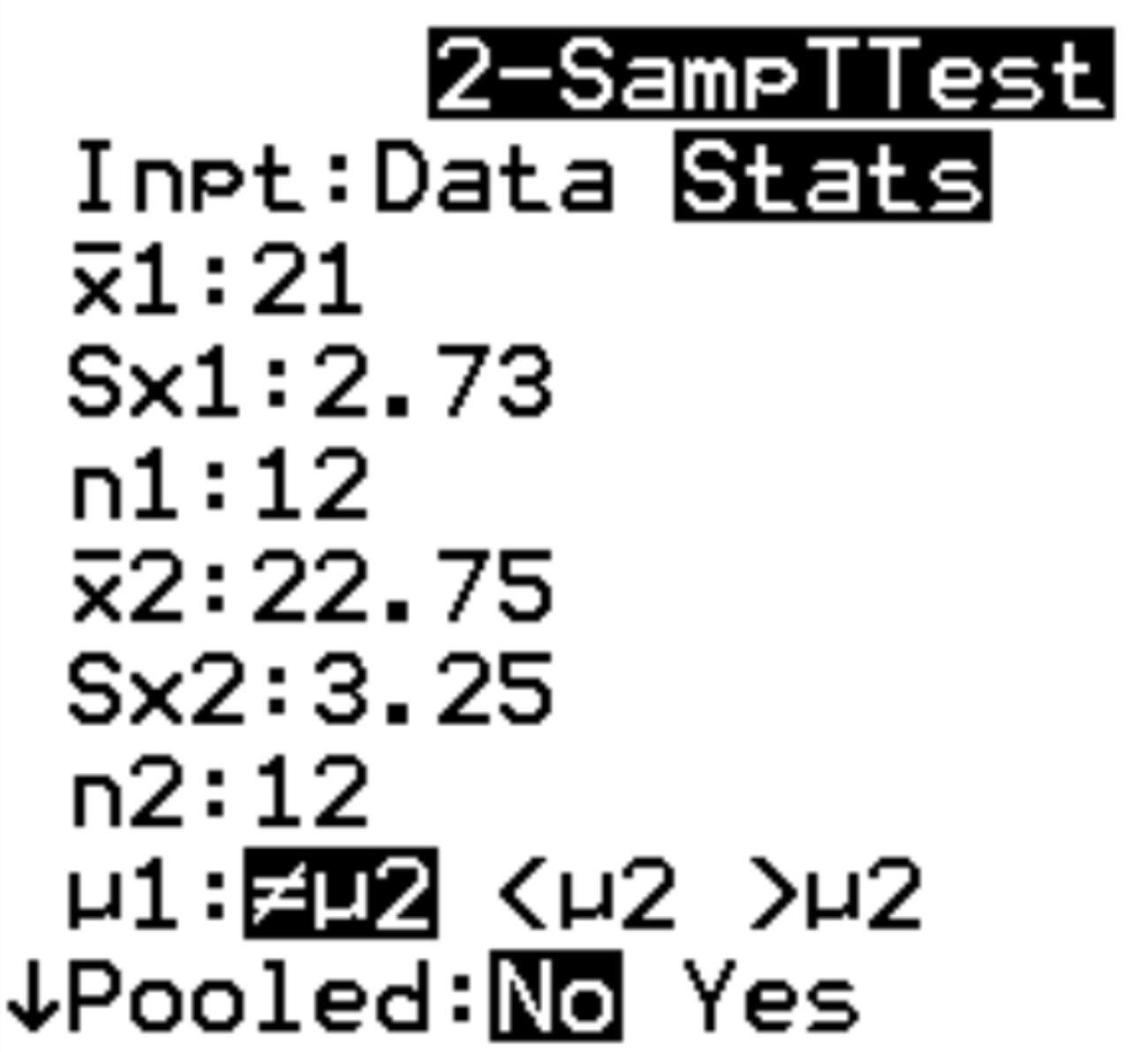
الخطوة 2: املأ المعلومات اللازمة.
سوف تطلب الآلة الحاسبة المعلومات التالية:
- الإدخال: اختر ما إذا كنت تعمل باستخدام البيانات الأولية (البيانات) أو الإحصائيات الموجزة (الإحصائيات). في هذه الحالة سوف نسلط الضوء على الإحصائيات ونضغط على ENTER .
- × 1 : متوسطات عينة المجموعة الأولى . سنكتب 21 ونضغط على ENTER .
- Sx1: الانحراف المعياري لعينة المجموعة الأولى. سنكتب 2.73 ثم نضغط على ENTER .
- n1: حجم عينة المجموعة الأولى. سنكتب 12 ونضغط على ENTER .
- × 2: متوسط عينة المجموعة الثانية. سنكتب 22.75 ثم نضغط على ENTER .
- Sx2: الانحراف المعياري لعينة المجموعة الثانية. سنكتب 3.25 ثم نضغط على ENTER .
- n2: حجم عينة المجموعة الثانية. سنكتب 12 ونضغط على ENTER .
- μ1 : الفرضية البديلة للاستخدام. نظرًا لأننا نجري اختبارًا ثنائي الطرف، فسوف نسلط الضوء على ≠ μ2 ونضغط على ENTER . يشير هذا إلى أن فرضيتنا البديلة هي μ1≠μ2. سيتم استخدام الخيارين الآخرين للاختبار الأيسر (μ1<μ2) واليمين (μ1>μ2).
- مُجمَّع: اختر ما إذا كنت تريد تجميع فجوات المجموعتين أم لا. في معظم الحالات سنختار لا. قم بتمييز لا ثم اضغط على ENTER .
أخيرًا، قم بتمييز حساب واضغط على ENTER .
الخطوة 3: تفسير النتائج.
ستنتج الآلة الحاسبة الخاصة بنا تلقائيًا نتائج مثالين لاختبار t:

وإليك كيفية تفسير النتائج:
- μ 1 ≠μ 2 : هذه هي الفرضية البديلة للاختبار.
- t=-1.42825817 : هذه هي إحصائية اختبار t.
- p=0.1676749174 : هذه هي القيمة p التي تتوافق مع إحصائية الاختبار.
- df=21.36350678: هذه هي درجات الحرية المستخدمة لحساب إحصائية الاختبار.
- س1 = 21 . هذا هو متوسط العينة الذي أدخلناه للمجموعة الأولى.
- × 2 = 22.75: هذا هو متوسط العينة التي أدخلناها للمجموعة الثانية.
- سكس1=2.73 . هذا هو نموذج الانحراف المعياري الذي أدخلناه للمجموعة الأولى.
- Sx2=3.25 : هذا هو نموذج الانحراف المعياري الذي أدخلناه للمجموعة الثانية.
- n1=12: هذا هو حجم العينة الذي أدخلناه للمجموعة الأولى.
- n2=12: هذا هو حجم العينة الذي أدخلناه للمجموعة الثانية.
وبما أن القيمة p للاختبار (0.1676749174) لا تقل عن 0.05، فإننا نفشل في رفض فرضية العدم. وهذا يعني أنه ليس لدينا ما يكفي من الأدلة لنقول أن متوسط ميلا في الغالون يختلف بين المجموعتين.